
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания к выполнению курсовой работы
3.1 Классический метод расчёта переходных процессов.
Расчёт переходных процессов классическим методом включает следующие этапы:
а) оределение независимых начальных условий:  .
.
Независимые начальные условия определяются путём расчета установившегося режима в цепи до коммутации и с применением законов коммутации:
 ;
; 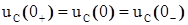 .
.
Так как в электрической цепи до коммутации действовал источник переменного синусоидального напряжения U(t)=Umsin(ωt+φu) (ключ находился в положении 1), то расчет установившихся значений UC(t) и iL(t) до коммутации осуществляют комплексным методом. Сначала определяют комплексные амплитуды напряжения на конденсаторе и тока в катушке, а затем переходят к их мгновенным значениям UC(t) и iL(t) и в полученные выражения подставляют t=0;
б) оределение принуждённого тока 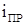 или принужденного напряжения
или принужденного напряжения 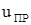 путём расчёта установившегося режима в цепи после коммутации.
путём расчёта установившегося режима в цепи после коммутации.
Принужденной режим цепи после коммутации (ключ находится в положении 2) обусловлен действием источника постоянного напряжения U0, поэтому принужденная составляющая тока 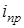 (или напряжения
(или напряжения  ) может быть найдена методами расчета цепей постоянного тока. Следует отметить, что сопротивление индуктивного элемента постоянному току равно нулю, а емкостного элемента – бесконечности;
) может быть найдена методами расчета цепей постоянного тока. Следует отметить, что сопротивление индуктивного элемента постоянному току равно нулю, а емкостного элемента – бесконечности;
в) запись выражения для искомого переходного тока или переходного напряжения в виде:
 ;
; 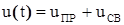 ;
;
г) запись дифференциальных уравнений по законам Кирхгофа для цепи после коммутации;
д) Определение свободного тока 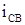 или напряжения
или напряжения  . Для определения
. Для определения 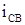 или
или  составляется характеристическое уравнение и находятся его корни. Характеристическое уравнения составляют наиболее простым методом входного сопротивления. Для этого записывают формулу комплексного входного сопротивления для цепи после коммутации
составляется характеристическое уравнение и находятся его корни. Характеристическое уравнения составляют наиболее простым методом входного сопротивления. Для этого записывают формулу комплексного входного сопротивления для цепи после коммутации  , в которой
, в которой  заменяют на р и полученное выражение входного операторного сопротивления приравнивают к нулю
заменяют на р и полученное выражение входного операторного сопротивления приравнивают к нулю 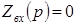 . После подстановки числовых значений параметров цепи рассчитывают корни характеристического уравнения – р1 ,р2 (цепь второго порядка).
. После подстановки числовых значений параметров цепи рассчитывают корни характеристического уравнения – р1 ,р2 (цепь второго порядка).
Запись выражения 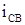 или
или  определяется типом корней характеристического уравнения. Выражение свободной составляющей тока
определяется типом корней характеристического уравнения. Выражение свободной составляющей тока  (или напряжения
(или напряжения 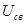 ) определяется видом корней характеристического уравнения
) определяется видом корней характеристического уравнения  . Если корни характеристического уравнения
. Если корни характеристического уравнения 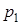 и
и  - различные и вещественные, то
- различные и вещественные, то 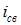 имеет вид
имеет вид  ,
,
где 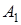 и
и 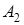 - постоянные интегрирования.
- постоянные интегрирования.
Если корни характеристического уравнения равны, т.е. 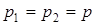 , то
, то 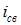 имеет вид
имеет вид  .
.
В случае комплексно-сопряженных корней характеристического уравнения 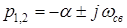 (
(  – собственное затухание,
– собственное затухание, 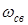 – частота свободных колебаний)
– частота свободных колебаний) 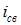 имеет вид
имеет вид 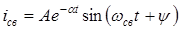 ,
,
где 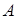 и
и 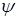 – постоянные интегрирования.
– постоянные интегрирования.
В цепях второго порядка для определения постоянных интегрирования используют начальные условия, причем независимые начальные условия определяют из законов коммутации 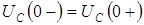 ,
,  , а зависимые начальные условия находят путем решения уравнений, составленных по законам Кирхгофа для цепи после коммутации при t=0;
, а зависимые начальные условия находят путем решения уравнений, составленных по законам Кирхгофа для цепи после коммутации при t=0;
ж) определение постоянных интегрирования по начальным значениям искомой величины и её первой производной (для цепи второго порядка).
3.2 Операторный метод расчёта переходных процессов.
Расчёт переходных процессов операторным методом включает следующие этапы:
а) Определение независимых начальных условий:  .
.
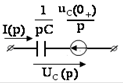
б) Составление эквивалентной операторной схемы (схема составляется для цепи после коммутации).
Т а б л и ц а 3.1
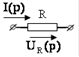
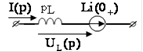
| Эквивалентные операторные схемы пассивных элементов | |
| Исходная схема | Операторная схема |
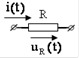
| 
|
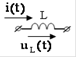
| 
|
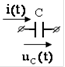
| 
|
в) Составление уравнений для определения изображения искомой величины, используя любой из методов расчёта: законы Кирхгофа в операторной форме, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора и т.п. (уравнения составляются для цепи после коммутации), и определение изображения искомой величины.
г) Определение искомой величины (оригинала) по найденному изображению, используя теорему разложения.
Т а б л и ц а 3.2
| Теорема разложения | |
Изображение имеет вид рациональной дроби: 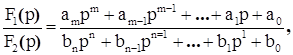 где m<n,
где m<n, 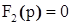 - характеристическое уравнение. Оригинал определяется по теореме разложения. - характеристическое уравнение. Оригинал определяется по теореме разложения.
| |
Вид корней характеристического уравнения 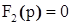 ,
для ,
для 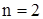 . .
| Теорема разложения |
корни характеристического уравнения 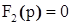 , , 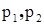 − вещественные и различные − вещественные и различные
| 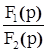  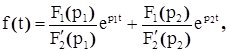 где
где 
|
корни характеристического уравнения 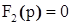 комплексные сопряженные комплексные сопряженные 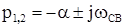
| 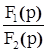  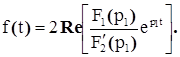
|
знаменатель имеет один нулевой корень: 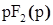 , корни характеристического уравнения , корни характеристического уравнения 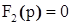 , , 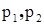 − вещественные и различные − вещественные и различные
| 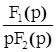   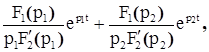
|
знаменатель имеет один нулевой корень: 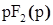 , корни характеристического уравнения , корни характеристического уравнения 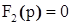 комплексные сопряженные комплексные сопряженные 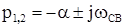
| 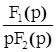   
|
Список литературы
1. Сборник задач по теоретическим основам электротехники/ Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-52 с.
2. Бессонов Л.А. Теоретические основы электротехники.-М.: Гардарики,1999. – 638 с.
3. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990.- 544 с.
4. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.- М.: Энергоатомиздат, 1989. -528 с.
5. Денисенко В.И., Зуслина Е.Х ТОЭ. Учебное пособие.- Алматы: АИЭС, 2000. – 83 с.
6. Денисенко В.И., Креслина С.Ю. ТОЭ1. Конспект лекций (для баколавриата 050702 – Автоматизация и управление). Алматы: АИЭС, 2008. – 67 с.
7. Денисенко В.И., Креслина С.Ю., Светашев Г.М. ТОЭ2. Конспект лекций (для бакалавриата 050702 – Автоматизация и управление). Алматы: АИЭС, 2009. – 62 с.
Содержание
| 1 Требования к выполнению и оформлению курсовой работы | |
| 2 Задание к курсовой работе | |
| 3 Методические указания к выполнению курсовой работы | |
| 4 Список литературы |
Сводный план 2013 г., поз. 24
Светлана Юрьевна Креслина
Алма Тулендиевна Аршабекова
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Методические указания и задания к курсовой работе
для студентов специальности 5В070200- Автоматизация и управление
Редактор: Л.Т. Сластихина
Специалист по стандартизации: Н.К. Молдабекова
Тираж __100___ экз. Бумага типографская
Подписано в печать _________ Формат 60х84 1/16 №1
Объем уч. - изд. л. Заказ ____. Цена тенге.
Копировально-множительное бюро
Некоммерческого акционерного общества
«Алматинский университет энергетики и связи»
050013, Алматы, Байтурсынова, 126
Дата добавления: 2014-12-30; просмотров: 365; Мы поможем в написании вашей работы!; Нарушение авторских прав |