
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
корреляционной модели
1. Проводится логический анализ сущности изучаемого явления и причинно-следственных связей в результате которого устанавливается результативный показатель и факторы, влияющие на его изменение.
2. Сбор первичной информации и проверка ее на однородность и нормальность распределения.
Однородная совокупность – совокупность у которой коэффициент вариации не превышает 33 %.
3. Исключение из массива первичной информации всех резко выделяющихся (аномальных) единиц по уровню признаков-факторов. На этом шаге исключаются единицы у которых уровень признака-фактора не попадает в интервал  .
.
4. Установление факта наличия корреляционной зависимости между результативным и факторным признаками и определяется ее характер и направление. Для установления наличия корреляционной связи существуют специальные методы, такие как:
– анализ параллельных рядов – сопоставляют две или несколько статистические величины. Например, сравним изменение возраста и рост у детей:
Таблица 38
| Возраст (мес.) | |||||||
| Рост (см) |
С увеличением возраста ребенка рост также увеличивается, следовательно связь прямая и ее можно описать либо уравнением прямой, либо параболы второго порядка;
– аналитические группировки – все единицы совокупности разбиваются на группы по величине факторного признака и для каждой группы определяется средняя величина результативного показателя, затем строится график эмпирической линии регрессии, по которой можно судить о наличии связи и ее форме;
– графический метод – на графике изображается поле корреляции. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.
5. Измерение степени тесноты связи и оценка ее существенности используют:
– Линейный коэффициент корреляции – применяют для парной линейной зависимости между двумя количественными признаками; его пределы [–1; +1];
– Коэффициент Фихнера – используют при небольшом объеме исходной информации, его пределы [–1; +1];
– Коэффициент ассоциации Д. Юла – для альтернативных признаков;
– Коэффициент взаимной сопряженности К. Пирсона – для альтернативных признаков, принимающих любое число вариантов значений, лежит в пределах [0; +1];
– Эмпирическое корреляционное отношение – при любой форме зависимости ([0; +1]);
– Коэффициент корреляции рангов Спирмена – когда значения количественных признаков могут быть проранжированны ([–1; +1]);
– Коэффициент контингенции К. Пирсона – для качественных (альтернативных) признаков ([–1; +1]);
– Коэффициент взаимной сопряженности А.А. Чупрова – при небольшом объеме исходной информации ([0; +1]).
Оценка существенности проводится по методам:
– t-критерий Стьюдента – при большом объеме выборки;
– метод преобразованной корреляции Фишера – по данным малой выборки
6. Построение модели связи (уравнения регрессии, параметры которого вычисляются по методу наименьших квадратов). Типы моделей рассматривались в рядах динамики.
Уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь, если отношение средней квадратической ошибки уравнения к среднему уравнению результативного признака не превышает 10-15%.
7. Изучение множественной корреляционной зависимости и отбор факторов, включаемых в модель множественной зависимости.
8. Включение отобранных факторов в модель множественной зависимости (число факторов, включаемых в модель должно быть в 5-6 раз меньше, чем число единиц, входящих в совокупность).
9. Определение коэффициента множественной (совокупной) корреляции.
Множественный коэффициент корреляции изменяется в пределах [0; + 1].
Частный коэффициент корреляции показывает тесноту линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель и изменяется в пределах [– 1; + 1].
Парный коэффициент корреляции показывает тесноту линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель и изменяется в пределах [– 1; + 1].
10. Определение коэффициента эластичности (показывает на сколько процентов в среднем изменяется результативный признак с изменением признака-фактора на 1 %) или β – коэффициента (показывает на какую часть среднего квадратическо отклонения изменится результативный показатель при изменении соответствующего фактора на величину его среднего квадратического отклонения).
Пример 29: В таблице приведены данные о ценах на золото и палладий в ноябре 2008г.
Таблица 39
| дата | золото | палладий | дата | золото | палладий |
| 02.11.2008 | 422,08 | 187,84 | 17.11.2008 | 444,09 | 218,12 |
| 03.11.2008 | 424,57 | 190,22 | 22.11.2008 | 454,38 | 227,06 |
| 09.11.2008 | 426,61 | 201,47 | 23.11.2008 | 449,24 | 218,70 |
| 10.11.2008 | 430,45 | 206,51 | 24.11.2008 | 453,05 | 217,96 |
| 11.11.2008 | 430,12 | 206,12 | 25.11.2008 | 456,53 | 219,18 |
| 14.11.2008 | 432,16 | 216,88 | 28.11.2008 | 459,28 | 225,80 |
| 15.11.2008 | 431,51 | 214,50 | 29.11.2008 | 456,89 | 223,87 |
| 16.11.2008 | 434,19 | 218,69 | 30.11.2008 | 454,61 | 220,82 |
Определите: 1) тесноту связи между ценами на золото и палладий; 2) параметры уравнения линейной регрессии, связывающей цену на золото и цену на палладий.
Решение:
Для измерения степени тесноты связи используется линейный коэффициент корреляции (n=16)
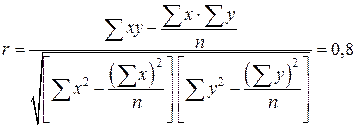
Все промежуточные вычисления приведены в таблице
| дата | золото | палладий | xy | x2 | y2 |
| 02.11.2005 | 422,08 | 187,84 | 79283,51 | 178151,53 | 35283,87 |
| 03.11.2005 | 424,57 | 190,22 | 80761,71 | 180259,68 | 36183,65 |
| 09.11.2005 | 426,61 | 201,47 | 85949,12 | 181996,09 | 40590,16 |
| 10.11.2005 | 430,45 | 206,51 | 88892,23 | 185287,20 | 42646,38 |
| 11.11.2005 | 430,12 | 206,12 | 88656,33 | 185003,21 | 42485,45 |
| 14.11.2005 | 432,16 | 216,88 | 93726,86 | 186762,27 | 47036,93 |
| 15.11.2005 | 431,51 | 214,50 | 92558,90 | 186200,88 | 46010,25 |
| 16.11.2005 | 434,19 | 218,69 | 94953,01 | 188520,96 | 47825,32 |
| 17.11.2005 | 444,09 | 218,12 | 96864,91 | 197215,93 | 47576,33 |
| 22.11.2005 | 454,38 | 227,06 | 103171,52 | 206461,18 | 51556,24 |
| 23.11.2005 | 449,24 | 218,70 | 98248,79 | 201816,58 | 47829,69 |
| 24.11.2005 | 453,05 | 217,96 | 98746,78 | 205254,30 | 47506,56 |
| 25.11.2005 | 456,53 | 219,18 | 100062,25 | 208419,64 | 48039,87 |
| 28.11.2005 | 459,28 | 225,80 | 103705,42 | 210938,12 | 50985,64 |
| 29.11.2005 | 456,89 | 223,87 | 102283,96 | 208748,47 | 50117,78 |
| 30.11.2005 | 454,61 | 220,82 | 100386,98 | 206670,25 | 48761,47 |
| Σ | 7059,8 | 3413,7 | 1508252,3 | 3117706,3 | 730435,6 |
Значение линейного коэффициента корреляции 0,8 свидетельствует о наличии прямой тесной связи.
Для определения параметров уравнения линейной регрессии используем формулы:
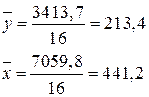
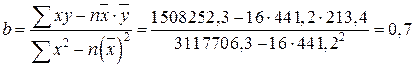
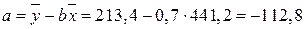
Модель связи следующая: 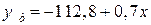
Дата добавления: 2014-12-23; просмотров: 366; Мы поможем в написании вашей работы!; Нарушение авторских прав |