
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Индексный метод изучения статистических совокупностей
Индексы средних величин. Рассмотрим индексы среднего уровня, их взаимосвязь и выявим роль факторов в динамике сложных явлений.
Часто в статистике необходимо изучать динамику явлений с помощью средних величин. Например, в экономике, в торговле приходится изучать изменение средней цены, среднего уровня издержек производства, средней заработной платы, средней себестоимости и т.д. При этом используются индексы среднего уровня.
Если среднее значение: 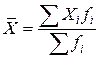 , то
, то  ,
,
где  – веса (численность) групп с равными уровнями осредняемого показателя
– веса (численность) групп с равными уровнями осредняемого показателя  .
.
Это индекс переменного состава, показывающий изменение среднего уровня 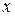 за два периода (отчетный и базисный) и за счет двух факторов–
за два периода (отчетный и базисный) и за счет двух факторов– 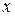 и
и  . Последнюю формулу можно переписать:
. Последнюю формулу можно переписать:
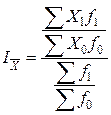 .
.
Однако средние величины отражают динамику не только самого усредняемого показателя по группам осреднения, но и изменения соотношения групп в общем итоге, то есть изменение структуры. Так, например, средняя зарплата может вырасти не только за счет роста ее у отдельных категорий работников, но и за счет роста удельного веса числа высокооплачиваемых квалифицированных работников. Средняя урожайность может вырасти за счет изменения структуры посевных площадей. Средняя цена товара может меняться в связи с изменением самой цены, так и изменения структуры продаж, то есть изменение удельного веса продаж дорогих изделий и т.д.
Для изучения влияния различных факторов на средний уровень изучаемого показателя используется индекс постоянного состава:
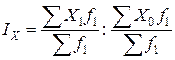 .
.
Индекс структурных сдвигов исчисляется по формуле:
 .
.
Данный индекс показывает влияние структуры ( 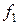 и
и  ) на изменение среднего уровня показателя, тогда последнюю формулу можно переписать:
) на изменение среднего уровня показателя, тогда последнюю формулу можно переписать:
 ,
,
 .
.
В символике коммерческой деятельности и статистике товарного обращения для средней цены эта последняя модель выглядит так:
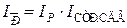 ,
,
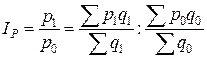 – индекс переменного состава,
– индекс переменного состава,
 – индекс цен постоянного (фиксированного) состава.
– индекс цен постоянного (фиксированного) состава.
 – общий индекс влияния структурных сдвигов на динамику средней цены.
– общий индекс влияния структурных сдвигов на динамику средней цены.
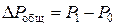 – общее абсолютное изменение средней цены (руб.).
– общее абсолютное изменение средней цены (руб.).
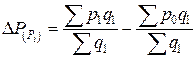 ‑ абсолютное изменение средней цены за счет изменения индивидуальных цен по отдельным товарам (руб.).
‑ абсолютное изменение средней цены за счет изменения индивидуальных цен по отдельным товарам (руб.).
 – абсолютное изменение средней цены за счет структуры продаж.
– абсолютное изменение средней цены за счет структуры продаж.
Если перейти от среднего уровня показателя к исчислению средних индексов, то по индивидуальным индексам можно исчислить агрегатный индекс:
 . Последняя ‑ формула средней гармонической взвешенной (т.е. по индивидуальным индексам можно найти общий, зная фактический оборот за текущий период). Или
. Последняя ‑ формула средней гармонической взвешенной (т.е. по индивидуальным индексам можно найти общий, зная фактический оборот за текущий период). Или  , т.к.
, т.к.  , то есть, зная оборот за первый период можно найти индекс физического объема товарооборота ‑ это средняя взвешенная арифметическая.
, то есть, зная оборот за первый период можно найти индекс физического объема товарооборота ‑ это средняя взвешенная арифметическая.
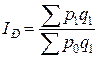 – общий индекс цен (индекс цен постоянного состава, индекс Пааше, агрегатный индекс цен).
– общий индекс цен (индекс цен постоянного состава, индекс Пааше, агрегатный индекс цен).
 – общий индекс физического объема товарооборота (индекс объема товарооборота в сопоставимых ценах, в неизменных ценах).
– общий индекс физического объема товарооборота (индекс объема товарооборота в сопоставимых ценах, в неизменных ценах).
 – общий индекс товарооборота в фактических (действующих) ценах.
– общий индекс товарооборота в фактических (действующих) ценах.
 ‑ абсолютное изменение объема товарооборота за счет изменения цен.
‑ абсолютное изменение объема товарооборота за счет изменения цен.
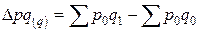 – абсолютное изменение объема товарооборота за счет изменения физической массы товаров.
– абсолютное изменение объема товарооборота за счет изменения физической массы товаров.
 ‑ общее изменение объема товарооборота.
‑ общее изменение объема товарооборота.
Базисные и цепные индексы.
В ряде случаев изучение динамики требует анализа развития экономики или социального явления не за два периода (текущего и базисного), а за несколько. В этом случае используется система индексов. При этом число исчисляемых индексов равно числу периодов минус единица.
Существует два варианта системы индексов.
1. Если в индексах знаменатель постоянный и характеризует уровень базисного периода, то сами индексы называются базисными (то есть сравнение идет с уровнями одного периода, взятого за базу).
2. Если индексы построены так, что каждый уровень (числитель) сравнивается с примыкающим к нему предшествующим уровнем (знаменатель) – то индексы называются цепными.
И базисные и цепные индексы могут быть с постоянным и переменным весом.
Цепной индекс:
с постоянным весом: 
с переменным весом: 
Базисный индекс:
с постоянным весом: 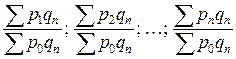
с переменным весом: 

Взаимосвязь между цепными и базисными индексами следующая:
 ,
,
где 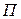 – символ произведения ценных индексов,
– символ произведения ценных индексов,
 – последний базисный индекс для всего ряда динамики.
– последний базисный индекс для всего ряда динамики.
Произведение цепных индексов дает базисный индекс последнего периода, причем расчет цепных и базисных индексов полностью аналогичен расчету темпов роста ряда динамики.
Дата добавления: 2014-12-23; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |