
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поквартальная продажа мяса в течение 6 лет по Ивановскому району, млн. руб.
| Годы | Поквартальные объемы перевозок, тыс. т. | Итого за год | |||
| I кв. | II кв. | III кв. | IV кв. | ||
| А | |||||
| 44,7 55,3 51,9 54,3 57,9 60,7 | 43,2 44,5 40,1 46,7 48,7 51,0 | 44,7 43,4 41,5 43,8 44,9 51,7 | 54,6 51,5 55,9 59,8 60,0 69,0 | 187,2 194,7 189,4 204,0 211,6 232,4 |
Таблица 34
| Годы | Поквартальные процентные отношения уровней ряда | Средние из квартальных отношений за год | |||
| I кв. | II кв. | III кв. | IV кв. | ||
| А | |||||
| – 101,28 100,78 97,14 96,82 101,17 | 96,64 80,47 77,26 86,00 84,11 84,02 | 103,47 97,53 103,49 93,79 92,20 101,37 | 122,15 118,66 134,70 136,53 133,63 133,46 | 107,42 99,49 104,10 103,37 101,69 105,01 | |
| Среднеквартальные отношения из цепных отношений за 6 лет | 99,44 | 84,75 | 98,64 | 129,86 | – |
| Преобразованная средняя | 100,00 | 84,75 | 83,6 | 108,56 | – |
| Преобразованная и исправленная средняя | 98,01 | 80,78 | 77,64 | 100,61 | 89,26 |
| Сезонная волна в среднем за 6 лет | 109,8 | 90,5 | 86,9 | 112,8 | 100,00 |
Цепные отношения вычисляются как процентные отношения объемов перевозок за каждый квартал к объему перевозок предшествующего квартала, в результате получается система относительных чисел, связанных в цепь.
1 кв. – 100%; 2 кв.:  ; 3 кв.:
; 3 кв.:  и т.д.
и т.д.
При отсутствии общей тенденции подъема или снижения произведение преобразованной средней за 4 кв. на среднюю из цепных отношений 1 кв. дает первоначальный уровень преобразования средней, т.е. 100; оно будет более 100, если наблюдается общая тенденция увеличения и, напротив, менее 100, если наблюдается общая тенденция уменьшения. Расхождение между произведением преобразованной средней за 4 кв. на среднюю из цепных отношений первого квартала и 100 – погрешность, возникшая в результате повышающейся или понижающейся общей тенденции, эту погрешность необходимо устранить. Наиболее простой способ устранения погрешности состоит в равномерном распределении ее на все кварталы. В нашем примере под влиянием растущей общей тенденции сезонные колебания оказались сдвинутыми на 7,95% (  ). Для получения исправленных сезонных колебаний необходимо из показателей первого квартала вычесть ј от 7,95 из 100 получается 98,01; для 2 кв. вычесть 2/4 от 7,95 из 84,75, будет 80,78; для 3 кв. вычесть ѕ от 7,95 из 83,6, получим 77,64 и для 4 кв. 4/4 от 7,95 из 108,56, получается 100,61. Далее вычисляется средняя квартальная, как средняя арифметическая из преобразованных и исправленных квартальных средних.
). Для получения исправленных сезонных колебаний необходимо из показателей первого квартала вычесть ј от 7,95 из 100 получается 98,01; для 2 кв. вычесть 2/4 от 7,95 из 84,75, будет 80,78; для 3 кв. вычесть ѕ от 7,95 из 83,6, получим 77,64 и для 4 кв. 4/4 от 7,95 из 108,56, получается 100,61. Далее вычисляется средняя квартальная, как средняя арифметическая из преобразованных и исправленных квартальных средних.
Сезонная волна в среднем за весь период исчисляется как процентное отношение преобразованных и исправленных средних за каждый квартал к их общей средней. Для 1 кв., например, она будет  , для второго –
, для второго – 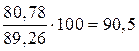 и т.д.
и т.д.
Таблица показывает сезонность перевозок, максимум перевозок приходится на 4 кв., а минимум на 3. На протяжении 6 лет в 4 кв. продавалось мяса на 12,8% больше среднеквартальной продажи, а в 3 кв. в среднем на 13,1% меньше.
1в. Метод У. Персонса: применяется в рядах динамики, отражающих развитие явлений, общая тенденция которых изменяется по средней геометрической, т.е. по сложным процентам. Суть этого метода заключается в исчислении показателей средней сезонной волны как медианных значений (а не как простых средних арифметических) из цепных отношений. Здесь погрешность, вызываемая влиянием общей тенденции, устраняется с помощью среднего коэффициента подъема (снижения) общей тенденции средней геометрической.
Алгоритм:
1. Вычисляются цепные отношения как процентные отношения каждого уровня ряда к уровню ряда предшествующего;
2. Вычисление средних, как медианные значения (медиана за первый отрезок времени принимается за 1 или 100%, а для остальных периодов средние исчисляются путем последовательного перемножения медианных средних). При перемножении преобразованного медианного значения за четвертый квартал на медианные значения первого квартала должна получиться единица (100%). Однако результат обычно бывает больше 1 или меньше ее, поскольку он отражает действительность, на развитие которой оказывает влияние общая тенденция увеличения или уменьшения.
Сезонная волна, исчисленная методом У. Персонса, более правильна, здесь из цепных отношений исчисляются медианные значения, а не средние арифметические, в связи с чем резкие случайные отклонения не сказываются на сезонной волне, они не принимаются в расчет.
Экстраполяция в рядах динамики. Условия корректности статистического прогноза.
Прогнозирование – это получение статистической оценки возможной меры развития явления (показателя, процесса, события) в будущем. Есть слово синоним термина прогнозирования – это экстраполяция – распространение выявленных в ряду динамики закономерностей на будущее (интерполяция – не путать – это нахождение недостающего члена на основе известных, рядом расположенных членов ряда распределения или ряда динамики).
Основой разработки прогноза является предположение, что закономерность или тенденция анализируемого ряда динамики (то есть, взятого за базу прогнозирования) сохраняются в дальнейшем. Это предопределяет точность прогноза.
Условием краткосрочного прогноза в рыночной экономике является стабильность и устойчивость, эволюционный (спокойный) характер функционирования экономики. При революционных, резких изменениях условий функционирования экономики прогнозирование становится невозможным. Например, невозможно в условиях финансового кризиса, денежной реформы, социальных конфликтов прогнозировать в торговле, в коммерции спрос и предложение, цены и др. Другим важным фактором точности прогноза является продолжительность срока прогнозирования. Чем короче сроки упреждения прогноза, тем точнее и надежнее результаты экстраполяции.
Метод прогнозирования на основе среднего абсолютного прироста. При исчислении уровня среднего абсолютного прироста в рядах динамики с числом членов ряда динамики, равным n, прогноз исчисляется:
 ,
,
где  – прогнозируемый уровень,
– прогнозируемый уровень,
 – конечный уровень базисного ряда,
– конечный уровень базисного ряда,
 – срок прогноза,
– срок прогноза,
 – средний абсолютный прирост.
– средний абсолютный прирост.
Метод прогнозирования на основе среднего темпа роста. При экстраполяции уровня развития изучаемого явления на основе среднего темпа роста применяется формула:

где  – средний темп роста
– средний темп роста
Метод прогнозирования на основе трендовой модели. Если разработана адекватная математическая модель общей тенденции развития явления, то прогнозирование заключается в экстраполяции расчетов по данной модели на период (  ). Например, для линейной модели производится расчет:
). Например, для линейной модели производится расчет:
 .
.
В силу того, что экстраполирование может привести к получению пессимистических прогнозных значений, что свидетельствует о нецелесообразности функционирования организации или предприятия, а потому целесообразно добиваться получение оптимистических результатов.
Дата добавления: 2014-12-23; просмотров: 301; Мы поможем в написании вашей работы!; Нарушение авторских прав |