
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выборочное наблюдение
Понятие о выборочном наблюдении. Как известно, все исследования связаны с большими материальными и временными затратами. Для оптимизации исследований производится отбор изучаемых единиц совокупности. Такие исследования принято называть несплошным наблюдением.
Совокупность единиц, из которых производится отбор, называют генеральной совокупностью,а совокупность отобранных единиц из генеральной совокупности – выборочной совокупностью.
Наиболее известным способом несплошного наблюдения является выборочное наблюдение. Выделим преимущества такого способа наблюдения:
- экономия времени и средств в результате сокращения объема работы;
- сведение к минимуму порчи или уничтожения исследуемых объектов (определение прочности пряжи при разрыве, испытание электрических лампочек на продолжительность горения, проверка консервов на доброкачественность);
- необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (при изучении бюджета семей);
- достижение большой точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации.
Можно утверждать, что выборочное наблюдение при строгом соблюдении условий случайности и достаточно большой численности отобранных единиц репрезентативно (представительно); по результатам изучения определенной части единиц с достаточной для практики степенью точности можно судить по всей совокупности.
Виды выборки.
I. По степени охвата единиц изучаемой совокупности:
1) большая выборка (  ≥ 30);
≥ 30);
2) малая выборка (  < 30).
< 30).
II. По методу отбора:
1) повторная – общая численность единиц генеральной совокупности не изменяется и каждая исследуемая единица может вновь попасть в выборку;
2) бесповторная – общая численность единиц генеральной совокупности меняется (сокращается) и исследуемая единица не может вновь попасть в выборку.
III По виду отбора:
1) индивидуальная – отбираются отдельные единицы генеральной совокупности;
2) групповая – отбираются качественно однородные группы изучаемых единиц;
3) комбинированная – сочетание первого и второго видов.
IV По способу отбора (формирования):
1) собственно случайная (простая случайная) – осуществляется путем жеребьевки, на основе таблиц случайных чисел и т.п. При этом каждой единице генеральной совокупности обеспечивается одинаковая вероятность (возможность) быть выбранной. Единица отбора совпадает с единицей наблюдения.
Случайный отбор может быть проведен в двух формах:
а) в форме возвратной (повторной) выборки – вероятность попадания каждой единицы генеральной совокупности остается постоянной, так как после отбора какой-то единицы она снова возвращается в генеральную совокупность и может быть выбранной;
б) в форме безвозвратной (бесповторной) выборки – выбранная единица не возвращается в генеральную совокупность и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастает).
Применение простой случайной повторной выборки на практике весьма ограниченно; обычно используется бесповторная выборка;
2) механическая – когда упорядоченно–расположенные единицы выбираются через определенные интервалы.
Механическая выборка заключается в отборе единиц из генеральной совокупности через равные промежутки из определенного расположения их в генеральной совокупности (по алфавиту, в пространстве, последовательности появления во времени). Такая выборка применяется при контроле качества различных продуктов.
При организации механического отбора возникают две задачи:
- определение «шага отчета» (интервала выборки);
- выбор единицы, с которой надо начинать отчет.
«Шаг отчета» определяется путем деления численности генеральной совокупности на численность выборочной совокупности  . Начала отчета находится путем случайного отбора из единиц первого интервала.
. Начала отчета находится путем случайного отбора из единиц первого интервала.
3) типическая (расслоенная или районированная) – всю совокупность предварительно разбивают на отдельные типические группы по какому-либо признаку, внутри группы проводится случайный или механический отбор в объеме пропорциональном численности единиц по группам в генеральной совокупности. Типический отбор обеспечивает наибольшую репрезентативность.
4) серийная (гнездовая) – производится отбор целых групп (серий, гнезд) единиц и внутри отобранных серий производится сплошное наблюдение. Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организационно, или, наконец, во времени. Отбор серий может производиться в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими. На практике чаще применяется серийный отбор с равными сериями.
5) комбинированная – предполагает использование нескольких способов выборки. Можно комбинировать, например, серийную выборку и случайную. В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц в серии. Такая комбинированная выборка может быть повторной (для групп и единиц) и бесповторной.
6) многоступенчатая выборка – предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. Выборка может быть двухступенчатой, когда генеральная совокупность разбивается на группы и производится отбор групп, а затем внутри групп — отбор единиц наблюдения. На обеих ступенях отбор может вестись в случайном порядке. В отличие от типического отбора, где отбор производится из всех без исключения групп, при многоступенчатом отборе производится отбор самих групп, и, следовательно, не все они попадают в выборку.
Основные показатели выборки.
Таблица 18
| Показатели | Определения | Генеральная совокупность | Выборочная совокупность |
| Объем генеральной совокупности | Численность единиц всей совокупности | N | – |
| Объем выборки | Число обследованных единиц | – | n |
| Генеральная средняя | Среднее значение признака в генеральной совокупности | 
| – |
| Выборочная средняя | Среднее значение признака в выборке | – | 
|
| Генеральная доля | Доля единиц обладающих данным значением признака в общем числе единиц генеральной совокупности | p | – |
| Выборочная доля | Доля единиц обладающих данным значением признака в общем числе единиц в выборке | – | 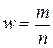
|
| Число единиц, обладающих изучаемым признаком | – | 
| |
| Генеральная дисперсия | Дисперсия признака в генеральной совокупности | 
| – |
| Выборочная дисперсия | Дисперсия признака в выборке | – | 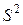
|
Ошибки выборки. Определение необходимого объема выборки Ошибка выборки  (ошибка репрезентативности) – это разность соответствующих выборочных и генеральных характеристик:
(ошибка репрезентативности) – это разность соответствующих выборочных и генеральных характеристик:
 – для средней количественного признака;
– для средней количественного признака;
 – для доли (альтернативного признака).
– для доли (альтернативного признака).
Величина этих отклонений называется ошибкой наблюдения,которая складывается из ошибок двоякого рода: ошибки регистрации (точности) и ошибки репрезентативности.
При помощи формул теории вероятности можно рассчитать возможную максимальную случайную ошибку – вероятный (стохастический) предел ошибки.
Максимально возможная ошибка – это такая величина отклонения выборочной средней (доли) от генеральной, вероятность превышения которой вследствие случайных причин в условиях данной выборки очень мала.
Величина случайной ошибки репрезентативности зависит от:
• степени колеблемости изучаемого признака в генеральной совокупности;
• способа формирования выборочной совокупности;
• объема выборки.
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе выборочных результатов. В каждой конкретной выборке расхождение между выборочной средней и генеральной может быть меньше средней ошибки выборки, равно ей или больше ее.
Предельную ошибку выборки можно найти на основе средней ошибки выборки:
 .
.
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:
 – для средней;
– для средней;
 – для доли.
– для доли.
Основные формулы для вычисления средних ошибок ( 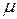 ) и необходимого объема выборки (
) и необходимого объема выборки (  ) приведены в таблице, с использованием следующих обозначений:
) приведены в таблице, с использованием следующих обозначений:
 ,
,  – межгрупповая дисперсия серийной выборки
– межгрупповая дисперсия серийной выборки
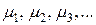 – средние ошибки выборки на отдельных ступенях отбора,
– средние ошибки выборки на отдельных ступенях отбора,
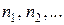 – численность выборок на соответствующих ступенях.
– численность выборок на соответствующих ступенях.
Таблица 19
Формулы для вычисления средних ошибок и необходимого объема выборки
| Вид отбора | Способ отбора единиц | Средняя ошибка μ | Объем выборки | ||
| для средней | для доли | для средней | для доли | ||
| Простая случайная выборка | повторный | 
| 
| 
| 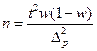
|
| бесповторный | 
| 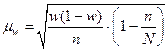
| 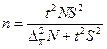
| 
| |
| Механическая выборка | Применяются формулы случайной бесповторной выборки | ||||
| Типическая выборка | повторный | 
| 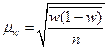
|  - для каждой группы; - для каждой группы;
 - число наблюдений в группе - число наблюдений в группе
| |
| бесповторный | 
| 
| |||
| Серийная выборка | повторный | 
| 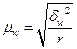
| В зависимости от целей исследования | |
| бесповторный | 
| 
| |||
| Комбинированная выборка | повторный | 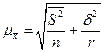
| В зависимости от комбинируемых методов | ||
| бесповторный | 
| ||||
| Многоступенчатая выборка | 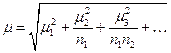
| В зависимости от целей исследования |
Элементы дисперсионного анализа. Дисперсионный анализ является одним из методов изучения влияния одного или нескольких факторных признаков на результативный признак. В зависимости от количества факторов дисперсионный анализ подразделяется на однофакторный и многофакторный. Ниже рассмотрено применение дисперсионного анализа для случая однофакторного комплекса.
В основе дисперсионного анализа лежит расчленение общей вариации изучаемого признака по источникам ее происхождения на два вида вариации:
систематическую вариацию, которая обусловлена изменением признака-фактора;
остаточную (случайную) вариацию, обусловленную действием прочих, случайных, не связанных с данным фактором обстоятельств.
Для разграничения этих вариаций всю совокупность наблюдавшихся единиц разбивают на группы (классы) по факторному признаку и исчисляют средние результативного признака по группам.
Групповые средние:
 ;
;
общая средняя:

где  – индивидуальные значения признака в группе;
– индивидуальные значения признака в группе;
 – число единиц, входящих в группу;
– число единиц, входящих в группу;
 – общее число наблюдений.
– общее число наблюдений.
Если сравнение групповых средних показывает определенное различие в их уровне, то необходимо установить, является ли это различие существенным и вызвано ли оно влиянием признака-фактора.
Для ответа на поставленный вопрос определяют два показателя дисперсии:
1) показатель 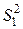 , характеризующий колеблемость групповых средних вокруг общей средней (межгрупповая дисперсия);
, характеризующий колеблемость групповых средних вокруг общей средней (межгрупповая дисперсия);
2) показатель  , отражающий остаточную, внутригрупповую дисперсию. Полученные показатели сравнивают, получая фактическое дисперсионное отношение:
, отражающий остаточную, внутригрупповую дисперсию. Полученные показатели сравнивают, получая фактическое дисперсионное отношение:

При дисперсионном анализе межгрупповую и внутригрупповую дисперсии определяют путем деления суммы квадратов отклонений на соответствующее число степеней свободы.
По таблице F-распределения Фишерапри определенном уровне значимости (или доверительной вероятности) и числе степеней свободы (  и
и  ) определяется табличное дисперсионное отношение (
) определяется табличное дисперсионное отношение (  ).
).
Если 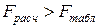 , то следует считать, что гипотеза о влиянии признака-фактора не опровергается.
, то следует считать, что гипотеза о влиянии признака-фактора не опровергается.
Пример 17: Пусть в регионе в порядке случайной бесповторной выборки было исследовано 100 предприятий из 1000 и получены следующие данные (таблица 1):
Требуется определить: 1) средний размер дивидендов, гарантируя результат с вероятностью 0,999; 2)долю предприятий, имеющих дивиденды более 745 руб., гарантируя результат с вероятностью 0,999.
Решение: 1) средний размер дивидендов лежит в доверительном интервале 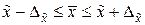 . Средний размер дивидендов в выборке находили ранее (517,45 руб.). Необходимо рассчитать предельную ошибку в выборке, для чего используем формулу простой случайной бесповторной выборки для средней (дисперсия была найдена ранее
. Средний размер дивидендов в выборке находили ранее (517,45 руб.). Необходимо рассчитать предельную ошибку в выборке, для чего используем формулу простой случайной бесповторной выборки для средней (дисперсия была найдена ранее  ,
,  ):
):
 руб.
руб.
Соответственно: 

2) Доверительные интервалы для генеральной доли:
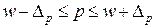
 – доля предприятий имеющих дивиденды более 745 руб.
– доля предприятий имеющих дивиденды более 745 руб.
Предельная ошибка доли
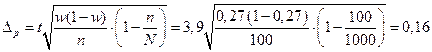
Соответственно: 

Пример 18: Фирма открыла два магазина по продаже товаров собственного изготовления в разных районах города. В результате механической выборки была зарегистрирована прибыль с единицы товара:
Таблица 20
| Прибыль с единицы товара, тыс.руб. | Количество проданного товара, шт. | |
| Магазин 1 | Магазин 2 | |
| 0,5 – 1,5 1,5 – 2,5 2,5 – 3,5 3,5 – 4,5 | – | |
| ИТОГО: |
Существенно ли расхождение прибыли с единицы товара в магазинах. Гарантировать результат с вероятностью 0,954.
Решение: Определим отношение:  , где
, где 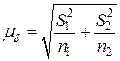
Промежуточные вычисления представим в таблице:
Таблица 21
| Прибыль с единицы товара, тыс.руб. | . Магазин 1 | |||||
| Количество проданного товара, шт | 
| 
| 
| 
| 
| |
| 0,5 – 1,5 | -1,5 | 2,25 | 13,50 | |||
| 1,5 – 2,5 | -0,5 | 0,25 | 3,25 | |||
| 2,5 – 3,5 | 0,5 | 0,25 | 2,50 | |||
| 3,5 – 4,5 | 1,5 | 2,25 | 18,00 | |||
| ИТОГО: | 37,25 | |||||
| Прибыль с единицы товара, тыс.руб. | . Магазин 2 | |||||
| Количество проданного товара, шт | 
| 
| 
| 
| 
| |
| 0,5 – 1,5 | -2,11 | 4,44 | 22,22 | |||
| 1,5 – 2,5 | – | – | – | – | – | – |
| 2,5 – 3,5 | -0,11 | 0,01 | 0,21 | |||
| 3,5 – 4,5 | 0,89 | 0,80 | 11,14 | |||
| ИТОГО: | 33,57 |
 ;
;  ;
; 
 , следовательно нулевая гипотеза не подтверждается, расхождение между прибылями существенно и не может быть объяснено случайностями выборки.
, следовательно нулевая гипотеза не подтверждается, расхождение между прибылями существенно и не может быть объяснено случайностями выборки.
Дата добавления: 2014-12-23; просмотров: 323; Мы поможем в написании вашей работы!; Нарушение авторских прав |