КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистическое изучение вариации. Понятие вариации. При изучении совокупности явления нельзя ограничиваться только нахождением средней величины
Понятие вариации. При изучении совокупности явления нельзя ограничиваться только нахождением средней величины. Средние величины дают обобщенную характеристику варьирующего признака, показывают типичные характеристики для изучаемой совокупности. Однако в средней величине не проявляется степень колеблемости отдельных значений признаков вокруг среднего уровня. В зависимости от однородности в совокупности колеблемость признаков может быть большой или малой. Поэтому возникает необходимость в измерении вариации отдельных вариантов по отношению к средней величине.
Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Вариация в переводе с латинского означает «колеблемость», «изменчивость», «непостоянство». Предполагая, что большинство социально-экономических явлений и процессов варьируют в некотором масштабе, статистика разработала методологию расчета показателей вариации, которые, в свою очередь, могут быть абсолютными, относительными и средними.
Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называют факторами. Нередко эти факторы действуют в противоположных направлениях и сами, в свою очередь, варьируют. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные, которые на одни единицы совокупности могут оказывать влияние, на другие нет.
Например, вариация оценок студентов на экзамене в вузе вызывается, в частности, различными способностями студентов; временем, затраченным ими на самостоятельную работу; посещаемостью занятий; различием социально-бытовых условий и т.д. Но на оценку могут влиять и какие-либо привходящие, чисто случайные причины, например, временное недомогание.
Вариация, порождаемая существенными факторами, носит систематический характер, то есть наблюдается последовательное изменение вариантов признака в определенном направлении. Такая вариация называется систематической. В систематической вариации проявляются взаимосвязи между явлениями, их признаками, в такой связи – один как причина, другой как следствие его действия.
Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариантов зависимого признака от случайных факторов; все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.
Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации.
Пример 13. Возьмем два варьирующих признака: возраст студентов и долю студентов дистанционного отделения среди обучающихся в одном из ВУЗов.
Таблица 15
| Возраст студента, лет | 18-22 | 23–28 | 29–34 | 35–40 | 41–46 |
| На 100 студентов дневного отделения приходится студентов дистанционного отделения |
Из данных таблицы видно, что от возраста студента зависит выбор формы обучения. Здесь наблюдается систематическая вариация зависимого признака. Оба признака варьируют, но вариация зависимого признака идет в противоположном направлении по сравнению с вариацией факторного признака. Чем больше возраст студента, тем ниже доля студентов дневной формы обучения.
Пример 13. В цехе работают две бригады, каждая из трех человек. Пусть заработная плата отдельного рабочего составила:
В первой бригаде – 9500, 10000, 10500 ( 
)
Во второй бригаде – 7500, 10000, 12500 ( 
).
Средняя зарплата одного рабочего в обеих бригадах одинакова и составляет 10000 шт., но колеблемость зарплаты отдельных рабочих в первой бригаде значительно меньше, чем во второй. Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.
Показатели вариации. К показателям вариации относятся: размах вариации, среднее линейное (абсолютное) отклонение (с.л.о.), дисперсия, среднее квадратическое отклонение (с.к.о.), коэффициент вариации.
1) Размах вариации – разность между максимальным и минимальным значением признака:
.
Он характеризует пределы изменения признака. В нашем примере размах вариации зарплаты для первой и второй бригад соответственно: 
=1000 шт., =5000 шт., что в 5 раз больше.
Это свидетельствует о том, что при численном равенстве средняя зарплата первой бригады более равномерна.
Средний размах: 
– это есть средняя арифметическая из ряда размахов, полученных из серии равных по объему наблюдений. Используется в контроле качества.
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.
Простейший показатель такого типа СЛО.
2) Среднее линейное отклонение (СЛО) – представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (учитывает только крайние значения признака и не учитывает все промежуточные).
– СЛО для несгруппированных данных: 
,
где 
– число членов ряда.
Т.е. 
– СЛО равно средней арифметической из абсолютных отклонений (модулей) признака всех единиц совокупности от средней арифметической.
– СЛО для сгруппированных данных: 
,
где 
– сумма частот вариационного ряда.
В формулах разности в числителе взяты по модулю, иначе в числителе всегда будет ноль – алгебраическая сумма отклонений вариантов от их средней арифметической.
Поэтому СЛО применяют редко, только в случаях, когда суммирование показателей без учета знаков имеет экономический смысл. Например, анализ состава рабочих, ритмичность производства, оборот внешней торговли.
3) Дисперсия – это средний квадрат отклонений индивидуальных значений от средней арифметической (не имеет единиц измерения).
В общем виде взвешенная дисперсия исчисляется по формуле:
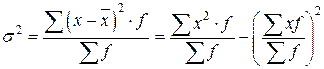
или простая дисперсия:
.
Дисперсия альтернативного признака:
Пример 14. Определить дисперсию, если из обследованных 2000 деталей 100 – бракованные.
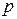– доля бракованных деталей, 
– доля годных деталей.
.
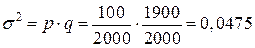4) Среднее квадратическое отклонение (СКО) ‑ это есть квадратный корень из среднего квадрата отклонений отдельных значений признака от средней арифметической:
– для несгруппированных данных;
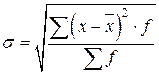– для сгруппированных данных (для вариационного ряда).
Коэффициент вариации. В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией зарплаты, выраженной в рублях.
Для осуществления такого сравнения, а также сравнения колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации – коэффициент вариации (КВ).
КВ – представляет собой выраженное в процентах отношение СКО к средней арифметической.
,
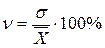это и есть коэффициент вариации. Это относительная мера вариации и позволяет сравнивать степень варьирования в разных вариационных рядах.
Рассмотрим расчет показателей вариации.
Пример 15. По исходным данным (таблица 1) определить: размах вариации, дисперсию, СКО, КВ.
Решение:
1) 
руб.
Остальные показатели требуют более трудоемких расчетов.
Таблица 17
| АО с размером дивидендов, руб | Число АО (  )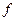
| Середина интервала (  )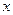
| 
| 
| 
| 
|
| 7 – 130 130 – 253 253 – 376 376 – 499 499 – 622 622 – 745 745 – 868 868 – 991 | 68,5 191,5 314,5 437,5 560,5 683,5 806,5 929,5 | 890,5 2201,5 5687,5 10484,5 | -448,95 -325,95 -202,95 -79,95 43,05 166,05 289,05 412,05 | 201556,1 106243,4 41188,7 6392,003 1853,303 27572,6 83549,9 169785,2 | 2620229,33 1274920,83 288320,92 83096,03 29652,84 330871,23 1086148,73 2376992,84 | |
| ИТОГО | – | – | – | 8090232,75 |
– среднее значение находили ранее, оно равно 517,45 руб.
2) дисперсия: 
.
3) СКО: 
руб.
4) КВ: 
.
Анализ полученных данных говорит о том, что размер дивидендов АО отличается от среднего размера ( =517,45) в среднем на 284 рубля, или на 55 %. Значение коэффициента вариации превышает 33 %, следовательно, вариация размера дивиденда велика, найденный средний размер дивиденда плохо представляет всю совокупность АО, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по размеру дивидендов.
Виды дисперсии.
Дисперсия – это средний квадрат отклонений всех значений признака ряда распределения от средней арифметической.
Свойства дисперсии:
1) Дисперсия постоянной величины равна нулю ( 
);
2) Дисперсия не меняется, если все варианты увеличить или уменьшить на одно и то же число (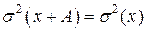 
);
3) Если все варианты умножить на число 
, дисперсия увеличится в 
раз 
;
4) Дисперсия от средней меньше, чем средний квадрат отклонений от любого числа 
на 
– свойство минимальности дисперсии от средней ( 
).
Использование свойств дисперсии позволяет упрощать ее расчеты, особенно в случаях, когда вариационный ряд составляет арифметическую прогрессию или имеет равные интервалы. В этих случаях сначала находят дисперсию от условного нуля, а затем используют 4-е свойство, переходят к дисперсии от средней.
Виды дисперсий для сгруппированных данных, условия их применения в статистических исследованиях.
Если совокупность данных сгруппирована на группы по какому-то признаку, то в этом случае выделяются 3 вида дисперсий:
- Общая дисперсия 
– Средняя из внутригрупповых дисперсий 
- Межгрупповая дисперсия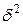 
Общая - измеряет вариацию во всей совокупности 
Средняя из внутригрупповых дисперсий исчисляется 
,
где 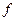– частота появления внутригрупповой дисперсии одной величины (одного размера).
– внутригрупповая 
- измеряет вариацию признака внутри группы, 
- групповая средняя.
Межгрупповая дисперсия 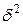– измеряет колеблемость групповых средних 
вокруг общей средней 
:
Она измеряет вариацию, обусловленную признаком, положенным в основу группировки.
Правило сложения дисперсий.
Общий закон (правило) сложения дисперсий ‑ Общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии.
Показывает значение фактора, положенного в основу группировки (из всей совокупности факторов).
Коэффициент детерминации – есть квадрат эмпирического корреляционного отношения.
Эмпирическое корреляционное отношение – есть корень квадратный из отношения межгрупповой дисперсии к общей:
– характеризует влияние группировочного признака на результативный признак (оба показателя (числитель и знаменатель) не превышают по своей величине единицы: чем больше показатели в этих пределах, тем теснее взаимосвязь между изучаемыми признаками).
; 
– влияние других факторов равно 0.
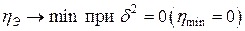– влияние признака равно 0.
Пример 16. Имеются следующие данные о размере дивидендов и прибыли компании:
Таблица 16
| АО с размером дивидендов, руб | Число АО | Прибыль в среднем на одно предприятие, млн.руб. |
| 7 – 130 130 – 253 253 – 376 376 – 499 499 – 622 622 – 745 745 – 868 868 – 991 | 46,0 75,0 240,0 40,0 38,4 245,0 80,0 45,0 | |
| ИТОГО: | 89,22 |
Определить: эмпирическое корреляционное отношение.
Решение: вычислим межгрупповую дисперсию по формуле:
.
Таблица 17
| АО с размером дивидендов, руб | Число АО | Прибыль в среднем на одно предприятие, тыс.руб.(  )
| 
| 
| 
|
| 7 – 130 130 – 253 253 – 376 376 – 499 499 – 622 622 – 745 745 – 868 868 – 991 | 46,0 75,0 240,0 40,0 38,4 245,0 80,0 45,0 | -43,22 -14,22 150,78 -49,22 -50,82 155,78 -9,22 -44,22 | 1868,31 202,32 22733,40 2423,00 2583,08 24266,16 85,08 1955,76 | 24288,08 2427,87 159133,82 31499,03 41329,26 291193,95 1106,07 27380,67 | |
| ИТОГО: | 89,22 | - | – | 578358,74 |
Теперь вычислим общую дисперсию выработки изделий на основе индивидуальных (несгруппированных) данных способом моментов: 
.
, тогда 
или 4%,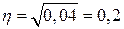 
.
Коэффициент детерминации говорит о том, что вариация прибыли АО на 4% зависит от вариации дивидендов и на 96% от прочих факторов.
Эмпирическое корреляционное отношение по своей величине далеко от единице, что свидетельствует о слабой связи между прибылью и дивидендами.
Дата добавления: 2014-12-23; просмотров: 28; Нарушение авторских прав
