Индексный метод в статистических исследованиях

Понятие о статистических индексах. В экономике и коммерции встречаются явления, которые нельзя суммировать. Например, нельзя суммировать цены разнородных товаров (бессмысленно), нельзя складывать данные учета движения разных товарных масс, так как они имеют разные единицы измерения (кг, штуки, пары, метры и т.д.). То есть реализация разнородной товарной массы в натурально-вещественной форме суммарному учету не подлежит (тоже бессмысленно). Вместе с тем экономически корректно задать такие вопросы, как: какова средняя тенденция изменения цен на разнородные товары, какова средняя тенденция реализации разнородных товаров в натуральном (физическом) выражении, то есть их физического объема. Все товары объединяет нечто общее, так как они участвуют в товарно-денежном обмене и все они имеют стоимостную форму. Поэтому для получения обобщающих суммарных величин по разнородным товарным массам используют именно их стоимостную форму. Это и делается в рамках индексного метода в статистике и экономике.

Индекс – это относительная величина сравнения уровней сложных показателей или отдельных их единиц, которые непосредственно не подлежат суммированию.

Когда рассматривается сопоставление уровней изучаемого явления во времени, то говорят об индексах динамики, в пространстве – о территориальных индексах, при сопоставлении с уровнем, например, договорных обязательств – об индексах выполнения обязательств и т.д.

Основным элементом индексного отношения является индексируемая величина.

Индексируемая величина – значение признака статистической совокупности, изменение которой является объектом изучения.

Основные задачи индексов:

1) измерение изменения сложных явлений (определение изменения физического объема всей продукции предприятия).

2) определение влияния отдельных факторов на изменение динамики сложного явления (например, влияние изменения уровня цен и изменения количества проданных товаров на объем товарооборота).

Таким образом, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами, планами, прогнозами и т.д. Например, интересно сравнить среднедушевое потребление какого-либо продукта в России и в развитых странах, а также провести сравнение с нормативом рационального питания.

Виды индексов. Индексы классифицируют по 3 признакам:

I. По содержанию изучаемых величин:

1. Индексы количественных показателей. Все индексируемые показатели этих индексов являются объемными, поскольку они характеризуют общий, суммарный размер (объем) того или иного явления и выражаются абсолютными величинами. При расчете таких индексов количества оцениваются в одинаковых, сопоставимых ценах (и. физического объема розничного товарооборота).

2. Индексы качественных показателей. Индексируемые показатели этих индексов характеризуют уровень явления в расчете на ту или иную единицу совокупности: цена за единицу продукции, себестоимость единицы продукции, зарплата одного работника и т.д. Такие показатели называют качественными, они носят расчетный, вторичный характер. Качественные показатели измеряют не общий объем, а интенсивность, эффективности явления или процесса. Как правило, они являются либо средними, либо относительными величинами. Расчет таких индексов производится на базе одинаковых, неизменных единиц совокупности.

II. По степени охвата элементов совокупности:

1. Индивидуальные индексы. Служат для характеристики изменения отдельных элементов сложного явления (например, изменение объема выпуска телевизоров определенной марки, рост или падение цен на акции в каком-либо акционерном обществе и т.д.).

2. Общие индексы. Отражают изменение всех элементов сложного явления. При этом под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объем продукции, включающий разноименные товары, цены на разные группы продуктов и т.д.).

3. Субиндексы, охватывающие не все элементы сложного явления, а лишь часть, их также называют групповыми (например, индексы физического объема продукции по отдельным отраслям промышленности).

III. По методам расчета общих индексов различают:

1. агрегатные.

2. средние.

Вычисление этих индексов составляет особый прием исследования, именуемый индексным методом.

Индексный метод имеет свою терминологию и символику. Каждая индексируемая величина имеет обозначение:

– количество (объем) какого-либо продукта в натуральном выражении;

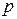– цена единицы товара;

– себестоимость единицы продукции;

– затраты времени на производство единицы продукции (трудоемкость);

– выработка продукции в стоимостном выражении на одного работника в единицу времени;

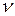– выработка продукции в натуральном выражении на одного работника или в единицу времени;

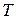– общие затраты времени ( ) или численность работников;

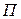– посевная площадь;

– урожайность отдельных культур и т.д.

– общая стоимость произведенной продукции данного вида или проданных товаров данного вида (товарооборот, выручка);

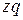– затраты на производство всей продукции (издержки производства);

- валовой сбор отдельной культуры.

Чтобы различать к какому периоду относятся индексируемые величины, принято возле символа индекса внизу справа ставить подстрочные знаки:

1, 2, 3 и т.д. – для сравниваемых (текущих) периодов;

0 – для базисных периодов (с которыми сравниваем).

Индивидуальные индексы обозначаются буквой i и снабжаются подстрочным знаком индексируемого показателя:

– индивидуальный индекс объема произведенной продукции отдельного вида или количества проданного товара данного вида;

– индивидуальный индекс цен и т.д.

Общий индекс обозначается – и также сопровождается подстрочным знаком индексируемого показателя.

Индивидуальные индексы относятся к одному элементу (явлению) и не требуют суммирования данных. Они представляют собой не что иное, как относительные величины динамики, выполнения обязательств, сравнения. Выбор базы сравнения определяется целью исследования.

Расчет индивидуальных индексов прост, их определяют вычислением отношения двух индексируемых величин:

- индивидуальный индекс физического объема продукции;

- индивидуальный индекс цен.

Индивидуальные индексы других показателей строятся аналогично. Значения индексов выражают в коэффициентах или процентах. Если из значения индекса, выраженного в процентах, вычесть 100%, то полученная разность показывает, на сколько процентов возросла (уменьшилась) индексируемая величина.

Методика расчета общих индексов сложнее, чем индивидуальных, и различна в зависимости от характера индексируемых показателей, наличия исходных данных и целей исследования.

Любые общие индексы могут быть построены двумя способами:

1) как агрегатные (агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава и индексы постоянного (фиксированного) состава);

2) как средние из индивидуальных:

– средние арифметические;

– средние гармонические.

Общие индексы количественных показателей.

1) Агрегатный индекс стоимости продукции (или товарооборота):

.

Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции.

Разность числителя и знаменателя формулы показывает, на сколько денежных единиц увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.

Значение индекса стоимости продукции зависит от двух факторов: изменения количества продукции и цен.

2) Индекс физического объема продукции – типичный индекс количественных показателей. Сложность при построении этого индекса заключается в том, что объемы разных видов продукции и товаров в натуральном выражении несоизмеримы и не могут суммироваться (нельзя складывать килограмм хлеба с литром молока). Поэтому для разнородных товаров нельзя построить индекс физического объема продукции и вычислить его как отношение простых сумм. Для этого требуются специальные приемы индексного метода.

В качестве общей меры – коэффициента соизмерения – используются качественные показатели (цена, себестоимость, трудоемкость). Умножая объем продукции каждого вида q на соответствующую цену, себестоимость, трудоемкость единицы продукции получают сравнимые показатели, которые можно суммировать.

Коэффициенты соизмерения обеспечивают количественную сравнимость, позволяют учитывать «вес» продукта в реальном экономическом процессе. Поэтому их показатели, связанные с индексируемыми величинами, принято называть весами индексов, а умножение на них – взвешиванием.

Умножением количества произведенной продукции на цену дает стоимостное выражение продукции каждого вида, которое можно суммировать. Формула данного индекса имеет вид .

Этот индекс получается устранением (элиминированием) в формуле агрегатного индекса стоимости продукции влияния изменения цены (т.е. фиксируем цену в числителе и знаменателе на уровне одного и того же периода).

В приведенной формуле индексируемой величиной является количество продукции, а весом – базисная цена.

Индекс физического объема продукции показывает, во сколько раз увеличился (уменьшился) физический объем продукции (т.е. количество товаров) или сколько процентов составляет его рост в отчетном периоде по сравнению с базисным периодом.

Абсолютное изменение физического объема продукции (т.е. на сколько денежных единиц (рублей) изменилась стоимость продукции в результате роста (уменьшения) ее физического объема q) вычисляется как разность между числителем и знаменателем формулы:

Изменение цен на продукцию в текущем периоде по сравнению с базисным не влияет на значение индекса.

При построении агрегатного индекса физического объема произведенной на предприятии продукции в качестве весов может быть использована себестоимость базисного периода:

,

этот индекс характеризует изменение издержек производства продукции в результате изменения физического объема ее производства.

Если имеющейся информации недостаточно для расчета общего агрегатного индекса (например, неизвестны количества произведенных отдельных видов продукции в натуральных измерителях, но известны индивидуальные индексы и стоимость продукции базисного периода), то исчисляют средний арифметический индекс физического объема продукции.

3) Средний арифметический индекс физического объема продукции:

где (стоимость отдельных видов продукции в базисном периоде) – вес.

4) Средний гармонический индекс физического объема продукции вычисляется, когда известны данные, позволяющие исчислить только числитель агрегатного индекса физического объема продукции. Выражая продукцию базисного периода как , производим замену в знаменателе агрегатной формы, получаем:

.

Общие индексы качественных показателей. Принцип построения агрегатных индексов качественных показателей рассмотрим на примере индекса цен. В этом случае индексируемой величиной будет цена товара, а весом – количество товаров одного из периодов (как правило, берут текущий период).

Агрегатный индекс цен с отчетными весами впервые предложен в 1874 г. немецким экономистом Пааше и носит его имя.

1) Формула агрегатного индекса цен Пааше выглядит следующим образом:

или

Индекс Пааше показывает, во сколько раз возрос (уменьшился) в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом.

2) Формула агрегатного индекса цен Ласпейреса (1864 г.):

.

Эти индексы для одних и тех же данных не совпадают, т.к. имеют различное экономическое содержание.

Индекс Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде, и фактическую экономию (перерасход) от изменения цен, т.е. индекс цен.

Индекс Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным по той продукции, которая была реализована в базисном периоде, и экономию (перерасход), которую можно было бы получить от изменения цен (т.е. во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде).

3) «Идеальный» индекс цен Фишера представляет собой среднюю геометрическую из произведения двух агрегатных индексов цен Ласпейреса и Пааше:

.

Идеальность формулы заключается в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный «обратный» индекс – это величина обратная величине первоначального индекса (этому условию отвечает любой индивидуальный индекс).

Однако геометрическая форма индекса имеет принципиальный недостаток: она лишена конкретного экономического содержания. Разность между числителем и знаменателем не покажет никакой реальной экономии или потерь из-за изменения цен.

Индекс Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно редко. Он используется при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения.

4) Средний гармонический индекс цен применяется в случаях, когда неизвестны отдельные значения и , но дано их произведение и индивидуальные индексы цен, а сводный индекс должен быть исчислен с отчетными весами. Этот индекс тождественен формуле Пааше:

.

Весами индивидуальных индексов в этом индексе служит стоимость отдельных видов продукции отчетного периода в ценах того же периода.

5) Средний арифметический индекс цен применяется, когда неизвестна цена отчетного периода, которая может быть найдена по формуле . Этот индекс тождественен агрегатному индексу Ласпейреса:

Весами усредняемых индивидуальных индексов в этом индексе служит объем товарооборота в базисном периоде .

Свойства общих индексов.

1. Синтетическое свойство. Общие индексы выражают относительные изменения сложных явлений, отдельные части и элементы которых непосредственно несоизмеримы.

2. Аналитическое свойство. Посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.