Степень ответственности зданий и сооружений

Степень ответственности зданий и сооружений определяется разме­ром материального и социального ущерба, возникающего в случае достижения ими предельного состояния. При проектировании это учитывают путём введения в расчёт коэффициента надёжности по назначению , значение которого зависит от класса ответственно­сти здания или сооружения. На коэффициент надо умножать расчётные значения нагрузок, усилий или иных воздействий.

СНиП 2.01.07-85* установлено три класса ответственности для зданий и сооружений:

- Класс I, = 1,0 и более; к этому классу относятся главные корпуса ТЭС, АЭС, телевизионные башни, промышленные трубы высо­той более 200 м, резервуары для нефти и нефтепродуктов вме­стимостью свыше 10 тыс. м³, крытые спортивные сооружения с трибунами, здания театров, кинотеатров, цирков, крытых рын­ков, учебных заведений, детских дошкольных учреждений, боль­ниц, родильных домов, музеев, государственных архивов и т. п.;

- Класс II, = 0,95; к этому классу относятся здания и со­оружения объектов, имеющих важное народнохозяйственное и (или) социальное значение (объекты промышленного, сельско­хозяйственного, жилищно-гражданского назначения и связи, не вошедшие в I и III классы);

- Класс III, = 0,9; к этому классу относятся здания и сооруже­ния, имеющие ограниченное народнохозяйственное и (или) со­циальное значение: склады без процессов сортировки и упаков­ки для хранения сельскохозяйственных продуктов, удобрений, химикатов, угля, торфа и др., теплицы, парники, одноэтажные жилые дома и т. п.

Численные значения коэффициента имеют вероятностно-эконо­мическое обоснование.

7. Нормативные и расчётные сопротивления бетона

Нормативные и расчетные сопротивления характеризуют прочностные качества материалов. С точки зрения математической статистики прочность бетона или арматуры является величиной случайной, колеблющейся в опреде­лённых пределах.

Прочностные характеристики бетона в силу существенной неод­нородности его структуры обладают значительной изменчивостью. За нормативное сопротивление бетона осевому сжатию прини­мают предел прочности осевому сжатию бетонных призм размерами 150´150´600 мм с обеспеченностью 0,95. Эта характеристика кон­тролируется путём проведения испытаний.

Под обеспеченностью понимают вероятность попадания случай­ных величин, выражающих прочность бетона, в интервал от R_bn до ∞.

Расчётное сопротивление бетона осевому сжатию для расчёта по предельным состояниям первой группы получают

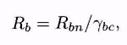
где = 1,3 — коэффициент надёжности по бетону при сжатии.

Аналогично определяется расчётное сопротивление бетона осе­вому растяжению для расчёта по предельным состояниям первой группы

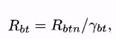
где γ_bt - коэффициент надёжности по бетону при растяжении; = 1,3 - при систематическом контроле прочности бетона при осевом растяжении; ⁼ 1,5 - при отсутствии такового.

Численные значения расчётных сопротивлений и для раз­личных классов бетона даны в СП 52-101-2003 (табл. 5.1 и 5.2).

Расчётные сопротивления бетона при расчёте по предельным со­стояниям первой группы назначены в нормах с высокой обеспечен­ностью равной 0,99865.

В необходимых случаях расчетные значения прочностных характеристик бетона умножают на следующие коэффициенты условий работы g_bi, учитывающие особенности работы бетона в конструкции (характер нагрузки, условия окружающей среды и т.д.):

а) g_b1 - для бетонных и железобетонных конструкций, вводимый к расчетным значениям сопротивлений R_b и R_bt и учитывающий влияние длительности действия статической нагрузки:

g_b1 = 1,0 - при непродолжительном (кратковременном) действии нагрузки;

g_b1 = 0,9 - при продолжительном (длительном) действии нагрузки;

б) g_b2 - для бетонных конструкций, вводимый к расчетным значениям сопротивления R_b и учитывающий характер разрушения таких конструкций,

g_b2 = 0,9.

в) g_b3 - для бетонных и железобетонных конструкций, бетонируемых в вертикальном положении при высоте слоя бетонирования свыше 1,5 м, вводимый к расчетному значению сопротивления бетона R_b ,

g_b3 = 0,85;

Наступление предельных состояний второй группы не столь опасно как первой, так как это обычно не влечёт за собой аварий, обрушений, жертв, катастроф. Поэтому расчётные сопротивления бетона для расчёта конструкций по предельным состояниям второй группы устанавливают при = = 1, т.е. принимают их равны­ми нормативным значениям

Как правило, здесь и 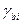= 1.

8. Нормативные и расчётные сопротивления арматуры

За нормативное сопротивление R_sn стержневой арматуры растяже­нию принимается наименьшее контролируемое значение предела те­кучести с обеспеченностью 0,95, т. е.

R_sn = σ_{y min}

Расчётные сопротивления арматуры растяжению для расчётов по предельным состояниям первой и второй группы определяют де­лением нормативных сопротивлений на соответствующие коэффи­циенты надёжности по арматуре, т. е.

где g_s - коэффициент надежности по арматуре, принимаемый равным:

для предельных состояний первой группы: 1,1 - для арматуры классов А240, А300 и А400; 1,15 – для арматуры класса А500; 1,2 - для арматуры класса В500; 1,0 - для предельных состояний второй группы, т. е.

Расчётное сопротивление стержневой арматуры классов A240, А300, A400 сжатию R_sc, используемые при расчётах по предельным состояниям первой группы, при наличии сцепления с бетоном при­нимают R_sc — R_s, так как при такой арматуре предел текучести стали при сжатии обычно достигается раньше разрушения сжатого железобетонного элемента.

9. Структура расчётных формул

В расчётах по несущей способности (по предельным состояниям пер­вой группы) исходят из стадии III напряжённо-деформированного состояния. При этом производится проверка выполнения условия

F F_ult

где F - вероятное наибольшее усилие, которое может возникнуть в элементе при исключительных, критических, но всё же возможных обстоятельствах;

F_ult - вероятная минимальная несущая способность элемента, определённая с учётом пониженной против контролируе­мой прочности бетона и арматуры.

Изменчивость величин F и F_ult как правило, описывается зако­ном нормального распределения случайных величин.

Подробнее условие можно записать так:

,

где С — коэффициент, учитывающий насколько точно выбранная расчётная схема отражает работу реальной конструкции и другие факторы;

S — коэффициент, учитывающий форму и размеры попе­речного сечения элемента.

Учтя, что g = g_n∙γ_fg и v = v_n ∙γ_fv , a R_b = , R_s = 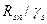, неравенство (2.15) можно записать несколько короче

Расчёт по перемещениям обычно заключается в определении прогиба конструкции от нагрузок с учётом их длительности дей­ствия и 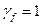и в сравнении его с предельно допустимым прогибом

f ≤ f_ult.

где f_ult — предельно допустимый прогиб по нормам для рассматри­ваемой конструкции.

Расчёт по раскрытию трещин заключается в определении ши­рины раскрытия трещин и сравнении её с предельно допустимой шириной раскрытия

a_crc ≤ a_crc,ult.

Расчет железобетонных элементов следует производить по продолжительному и по непродолжительному раскрытию нормальных и наклонных трещин.

Ширину продолжительного раскрытия трещин определяют по формуле:

a_crc = a_crc1,

а непродолжительного раскрытия трещин - по формуле

a_crc = a_crc1 + a_crc2 - a_crc3,

где a_crc1 - ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;

a_crc2 - ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;

a_crc3 - ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.

Считается, что трещины не появляются, если усилие N от дей­ствия внешних нагрузок не превосходит усилия F_crc,ult, т.е.

F ≤ F_crc,ult

где F_crc,ult — усилие, воспринимаемое сечением в момент, предшеству­ющий образованию трещин.

Метод расчёта по предельным состояниям называют полуверо­ятностным. Большинство величин, входящих в расчётные форму­лы, являются величинами случайными. Нормативные значения на­грузок и воздействий, а также сопротивлений материалов обоснова­ны с позиций теории вероятностей. Однако проектировщик пользу­ется конкретными детерминированными величинами, полученными на основании теории вероятностей. Таким образом, теория вероят­ностей используется в нормах проектирования строительных кон­струкций в неявной форме, что послужило основанием метод рас­чёта по предельным состояниям называть полувероятностным.

Основная идея метода расчёта по предельным состояниям за­ключается в обеспечении гарантии того, чтобы даже в тех редких случаях, когда на конструкцию действуют максимально возмож­ные нагрузки, прочность бетона и арматуры минимальна, а условия эксплуатации весьма неблагоприятны, конструкция не разрушалась или не получала бы недопустимых прогибов или трещин.

Достоинства метода:

1. Введением в расчёты вместо единого коэффициента запаса проч­ности системы расчётных коэффициентов, учитывающих диф­ференцированно влияние на несущую способность элемента из­менчивости нагрузок, прочностных свойств материалов, условий эксплуатации, класса ответственности достигают лучшей сходи­мости теоретических данных с опытными, чем при едином коэф­фициенте запаса k в прежних методах расчёта.

2. Каждое новое достижение в повышении однородности матери­алов может быть учтено в нормах, что приведёт к их экономии.

3. Конструкции, рассчитанные по предельным состояниям, получа­ются несколько экономичнее по расходу материалов.

Недостатки метода:

2. Некоторые коэффициенты метода не получили достаточного опытного обоснования. Так, например, одинаковый коэффициент надёжности по нагрузке для собственного веса приме­няемый как для большепролётных тонкостенных покрытий типа оболочек, где нагрузка от массы покрытия является основной, так и для междуэтажных перекрытий, которые работают на зна­чительную временную нагрузку, недостаточно обоснован.

3. Определение несущей способности элементов, состоящих из двух и более материалов (например, железобетонных) выполняется в настоящее время без учёта совместного статистического раз­броса прочности этих материалов при расчётных сопротивлени­ях, соответствующих низкой прочности каждого материала. Ве­роятность обнаружить материал с прочностью ниже расчётно­го сопротивления приблизительно равна 0,001. Вероятность сов­местного невыгодного попадания арматуры и бетона минималь­ной прочности является величиной чрезвычайно малой (пример­но 2 • 10^-6), которая практически не может встретиться в экс­плуатируемых конструкциях. В связи с этим запроектированные по нормам конструкции обладают дополнительными резервами прочности, которые не учитываются в расчётах.