
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ НА ПОЧНОСТЬ ПО СЕЧЕНИЯМ НОРМАЛЬНЫМ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
1. Предпосылки расчёта на прочность по нормальным сечениям
2. Расчёт изгибаемых элементов прямоугольного сечения с одиночной арматурой
3. Понятие о минимальном проценте армирования
4. Типы задач по расчёту изгибаемых элементов прямоугольного сечения
1. Предпосылки расчёта на прочность по нормальным сечениям
- в основу расчета положена третья стадия работы железобетонного элемента – стадия разрушения;
- расчётное сечение принимается по трещине, т.е растянутую зону бетона при расчёте не учитывают;
- фактическую криволинейную эпюру напряжений в сжатой зоне бетона высотой хфи краевой ординатой >Rb заменяют эквивалентной по усилию прямоугольной эпюрой напряжений высотой хи краевой ординатой Rb (х = 0,8хф; хф = 1,25х);
- растягивающие напряжения в арматурев момент исчерпания сечением балки несущей способности принимают не более величины расчётного сопротивления арматуры на растяжение - Rs.
- сжимающие напряжения в арматуре в момент исчерпания сечением балки несущей способности принимают не более величины расчётного сопротивления арматуры на сжатие - Rsс ;
- расчёт на прочность производят в зависимости от соотношения значений фактической (х) и граничной(хR) высот сжатой зоны бетона или их относительных значений ξ = х / h0и ξR = хR / h0, где h0 – рабочая высота сечения – расстояние от крайнего сжатого волокна бетона до центра тяжести растянутой арматуры.
Возможны два случая расчёта изгибаемых железобетонных элементов. Первый случай расчёта при х ≤ хR (ξ ≤ ξR) – разрушение элемента происходит по растянутой зоне. Второй случай расчёта при х > хR (ξ > ξR) – разрушение элемента происходит по сжатой зоне.
Для вычисления граничной относительной высоты сжатой зоны бетона (  ) находим h0 = h – a , где a = 0,1h (рис. 10).
) находим h0 = h – a , где a = 0,1h (рис. 10).
Из условия совместности деформаций бетона и стали (из подобия треугольников эпюры деформаций) получим 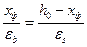 . Учитывая, что
. Учитывая, что 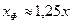 , имеем
, имеем 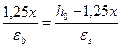 или
или 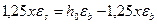 .
.

Рисунок 7.1 – К определению граничной высоты сжатой зоны бетона
Разделив обе части уравнения на 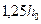 , получим
, получим 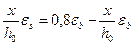 или
или 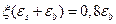 , отсюда
, отсюда 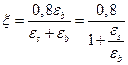 .
.
При одновременном достижении предельных напряжений в арматуре и бетоне получим формулу для определения относительной граничной высоты сжатой зоны бетона:
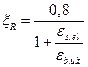 ,
,
где εs,el – относительная деформация растянутой арматуры при напряжениях, равных Rs, определяемая по формуле 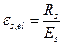 .
.
Значение модуля упругости арматуры Es принимают одинаковым при растяжении и сжатии и равными Es= 2,0∙105 мПа;
εb,ult – относительная деформация сжатого бетона при напряжениях, равных Rb, принимаемая равной 0,0035.
2. Расчёт изгибаемых элементов прямоугольного сечения с одиночной арматурой
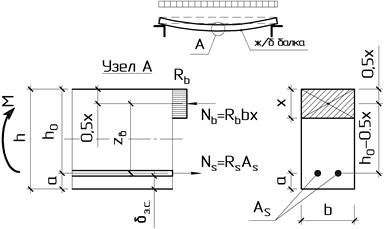
Рисунок 7.2 – Схема усилий при расчёте прочности изгибаемого элемента прямоугольного сечения с одиночной арматурой по нормальному сечению
Равнодействующие нормальных напряжений в сжатом бетоне и в растянутой арматуре определим по следующим формулам:
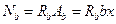 ,
, 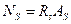 .
.
В соответствие с рис. 11 плечо внутренней пары сил равно
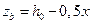 .
.
Рассмотрим равновесие элемента (рис. 11) под действием изгибающего момента от нагрузки М и внутренних усилий, возникающих в сжатом бетоне Nb и растянутой арматуре Ns.
1. 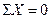 - сумма проекций, действующих сил на ось балки.
- сумма проекций, действующих сил на ось балки.
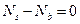 ;
; 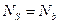 ;
; 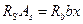 .
.
Высота сжатой зоны бетона равна 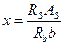 .
.
Подставив в эту формулу значение 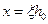 , получим
, получим 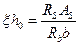 и
и  выразим отсюда площадь поперечного сечения растянутой арматуры
выразим отсюда площадь поперечного сечения растянутой арматуры
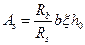 .
.
Из выражения 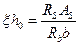 получим
получим  . Обозначим отношение площади сечения арматуры к площади сечения бетона
. Обозначим отношение площади сечения арматуры к площади сечения бетона 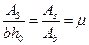 коэффициентом армирования сечения, тогда
коэффициентом армирования сечения, тогда 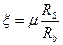 или
или  .
.
Процент армирования сечения 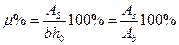 или
или 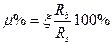 .
.
2.  - сумма моментов, действующих сил относительно центра тяжести растянутой арматуры.
- сумма моментов, действующих сил относительно центра тяжести растянутой арматуры.
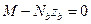 ;
; 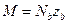 ;
; 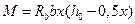 . Выражение
. Выражение 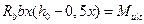 представляет собой выраженный через параметры сжатого бетона предельный изгибающий момент, воспринимаемый данным сечением, который называют несущей способность сечения.
представляет собой выраженный через параметры сжатого бетона предельный изгибающий момент, воспринимаемый данным сечением, который называют несущей способность сечения.
Тогда условие прочности изгибаемого элемента по нормальному сечению на действие изгибающего момента примет вид
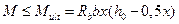 .
.
Таким образом, прочность элемента достаточна, если внешний расчётный изгибающий момент не превосходит расчётной несущей способности сечения, выраженной в виде обратно направленного момента внутренних сил.
Выполнив подстановку 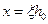 , получим
, получим
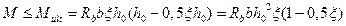 .
.
Обозначив 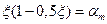 , получим условие прочности изгибаемого элемента в другом виде
, получим условие прочности изгибаемого элемента в другом виде
 .
.
Приравняв внешний и внутренний моменты 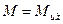 , можно определить рабочую высоту сечения элемента
, можно определить рабочую высоту сечения элемента  или коэффициент
или коэффициент  .
.
3.  - сумма моментов относительно центра тяжести сжатой зоны бетона.
- сумма моментов относительно центра тяжести сжатой зоны бетона.
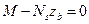 ;
; 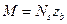 ;
; 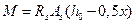 .
.
Выражение 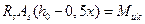 представляет собой выраженный через параметры растянутой арматуры предельный изгибающий момент, воспринимаемый данным сечением, который тоже называют несущей способность сечения.
представляет собой выраженный через параметры растянутой арматуры предельный изгибающий момент, воспринимаемый данным сечением, который тоже называют несущей способность сечения.
Тогда условие прочности изгибаемого элемента по нормальному сечению на действие изгибающего момента примет вид
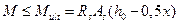 .
.
Выполнив подстановку 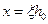 , получим условие прочности изгибаемого элемента в другом виде
, получим условие прочности изгибаемого элемента в другом виде
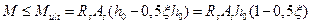 .
.
Коэффициент 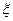 определим из выражения
определим из выражения 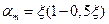 ,
,
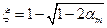 .
.
Приравняв внешний и внутренний моменты 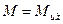 , можно определить площадь поперечного сечения растянутой арматуры
, можно определить площадь поперечного сечения растянутой арматуры
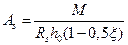 .
.
Приведённые выше формулы справедливы при условии 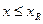 или
или 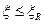 , т.е. когда разрушение элемента происходит по растянутой зоне.
, т.е. когда разрушение элемента происходит по растянутой зоне.
Если разрушение элемента происходит по сжатой зоне, т.е.  >
> 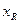 или
или 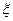 >
> 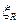 , то максимальный предельный изгибающий момент, воспринимаемый прямоугольным сечением, определяют исходя из значения граничной высоты сжатой зоны бетона
, то максимальный предельный изгибающий момент, воспринимаемый прямоугольным сечением, определяют исходя из значения граничной высоты сжатой зоны бетона 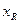 , которой соответствуют величины
, которой соответствуют величины 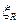 ,
, 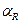 ,
, 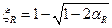 , тогда
, тогда
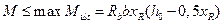 ,
,
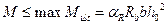 .
.
В случае если 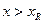 определить максимальный предельный изгибающий момент через характеристики арматуры по формулам
определить максимальный предельный изгибающий момент через характеристики арматуры по формулам 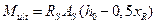 или
или 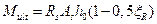 не допустимо, так как растягивающие напряжения в арматуре
не допустимо, так как растягивающие напряжения в арматуре  , что определяется совместностью деформаций. Таким образом, в случае
, что определяется совместностью деформаций. Таким образом, в случае 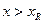 несущая способность арматуры на растяжение используется не полностью. Разрушение изгибаемого элемента в этом случае носит мгновенный, хрупкий характер, вследствие исчерпания несущей способности бетона сжатой зоны, а напряжения в арматуре при этом не достигают предела текучести
несущая способность арматуры на растяжение используется не полностью. Разрушение изгибаемого элемента в этом случае носит мгновенный, хрупкий характер, вследствие исчерпания несущей способности бетона сжатой зоны, а напряжения в арматуре при этом не достигают предела текучести 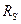 .
.
Определение предельного изгибающего момента, воспринимаемого прямоугольным сечением, представим в таблице 1.
Таблица 1
1–й случай расчёта
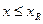
| 2–й случай расчёта 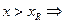 расчёт выполняем при расчёт выполняем при 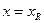
|
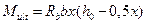
| 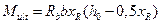
|
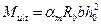
| 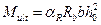
|
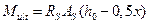
| |
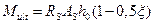
|
Дата добавления: 2014-12-30; просмотров: 472; Мы поможем в написании вашей работы!; Нарушение авторских прав |