
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разрушение бетонной полосы между наклонными трещинами.
Причина разрушения – совместное действие в двух взаимно-перпендикулярных направлениях главных сжимающих и растягивающих напряжений. Происходит разрушение бетона, который находится в сложном напряжённом состоянии – двухосном сжатии-растяжении (рис. 9.3).

Рисунок 9.3 – Схема разрушения изгибаемых элементов по бетонной полосе между трещинами от совместного действия сжимающих (σ1) и растягивающих (σ2) напряжений.
Сущность расчёта изгибаемых элементов по наклонным сечениям заключается в проверке прочности сжатой бетонной полосы между наклонными трещинами и прочности наклонных сечениё на действие поперечной силы, а так же изгибающего момента.
2. Расчёт изгибаемых элементов по сжатой бетонной полосе между наклонными сечениями
Расчёт производят из условия
 ,
,
где 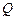 – поперечная сила в нормальном сечении, принимаемая на расстоянии от опоры не менее
– поперечная сила в нормальном сечении, принимаемая на расстоянии от опоры не менее  ;
;
 = 0,3 для тяжёлого бетона.
= 0,3 для тяжёлого бетона.
Если 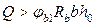 , то необходимо повысить класс бетона или (и) размеры поперечного сечения балки, в первую очередь ширину сечения
, то необходимо повысить класс бетона или (и) размеры поперечного сечения балки, в первую очередь ширину сечения  .
.
3. Расчёт изгибаемых элементов по наклонным сечениям на
действие поперечных сил (расчёт поперечной арматуры)
Расчёт поперечной арматуры необходим, если выполняется условие 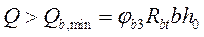 ,
,
где  для тяжёлого бетона.
для тяжёлого бетона.
Если 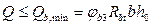 , то расчёт поперечной арматуры не нужен, и тогда её устанавливают по конструктивным требованиям.
, то расчёт поперечной арматуры не нужен, и тогда её устанавливают по конструктивным требованиям.
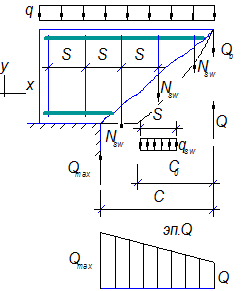
Рисунок 9.4 – Схема усилий в наклонном сечении при расчёте его на действие поперечной силы
Рассмотрим равновесие элемента (рис. 3) и спроецируем действующие усилия на вертикальную ось.

 , (*)
, (*)
 ,
,
где 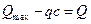 - поперечная сила в конце наклонного сечения с длиной проекции с на продольную ось элементаот внешней нагрузки;
- поперечная сила в конце наклонного сечения с длиной проекции с на продольную ось элементаот внешней нагрузки;
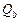 – поперечная сила, воспринимаемая бетоном в наклонном сечении;
– поперечная сила, воспринимаемая бетоном в наклонном сечении;
 - поперечная сила, воспринимаемая поперечными стержнями в наклонном сечении.
- поперечная сила, воспринимаемая поперечными стержнями в наклонном сечении.
Подставив Q, Qb, Qsw в исходное уравнение (*) получим условие прочностиизгибаемого элемента по наклонному сечению на действие поперечной силы
 .
.
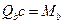 – момент силы, воспринимаемой бетоном, относительно начала наклонного сечения, который принимают равным
– момент силы, воспринимаемой бетоном, относительно начала наклонного сечения, который принимают равным  (
(  = 1,5 для тяжёлого бетона). Тогда
= 1,5 для тяжёлого бетона). Тогда 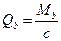 .
.
Значение поперечной силы, воспринимаемой бетоном в наклонном сечении принимают
 .
.

Где  = 0,75 для тяжёлого бетона;
= 0,75 для тяжёлого бетона;
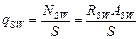 - поперечное усилие в стержнях на единицу длины элемента;
- поперечное усилие в стержнях на единицу длины элемента;
S – шаг поперечных стержней вдоль элемента.
с0 – длина проекции наклонной трещины на продольную ось элемента, принимаемая равной
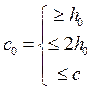 .
.
Преобразуем исходное выражение (*)
 ,
,
где 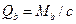 и
и  ,
,
тогда

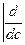 .
.
Продифференцируем данное выражение по  при
при  , что соответствует минимальному значению несущей способности элемента по поперечной силе:
, что соответствует минимальному значению несущей способности элемента по поперечной силе: 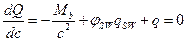 .
.
Тогда
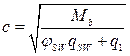 ≤
≤  ,
,
где: 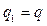 , если действует сплошная равномерно распределённая нагрузка
, если действует сплошная равномерно распределённая нагрузка  ;
;
 , если нагрузка
, если нагрузка  включает в себя временную нагрузку
включает в себя временную нагрузку 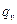 .
.
При действии на элемент сосредоточенных сил значение  принимают равным расстояниям от опоры до точек приложения этих сил, а так же равным
принимают равным расстояниям от опоры до точек приложения этих сил, а так же равным 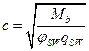 , но не меньше
, но не меньше 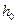 , если это значение меньше расстояния от опоры до 1-го груза.
, если это значение меньше расстояния от опоры до 1-го груза.
Если  , следует принимать
, следует принимать 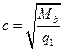 .
.
Поперечную арматуру учитывают в расчёте, если соблюдается условие 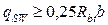 .
.
При расчёте поперечной арматуры обычно задаются диаметром поперечных стержней 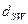 и их шагом
и их шагом  вдоль элемента по конструктивным требованиям, вычисляют
вдоль элемента по конструктивным требованиям, вычисляют  и
и , и проверяют условие прочности изгибаемого элемента по наклонному сечению на действие поперечной силы
, и проверяют условие прочности изгибаемого элемента по наклонному сечению на действие поперечной силы
 .
.
При этом шаг поперечных стержней, учитываемых в расчёте, должен быть не более 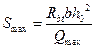 .
.
В случае не обеспечения по расчёту прочности наклонного сечения при первоначально принятых исходных данных (шаг поперечных стержней  , диаметр поперечных стержней
, диаметр поперечных стержней 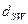 ), требуется увеличить диаметр поперечных стержней или (и) уменьшить их шаг и повторно выполнить проверочный расчёт.
), требуется увеличить диаметр поперечных стержней или (и) уменьшить их шаг и повторно выполнить проверочный расчёт.
4. Расчёт изгибаемых элементов по наклонным
Дата добавления: 2014-12-30; просмотров: 320; Мы поможем в написании вашей работы!; Нарушение авторских прав |