РАЗДАТОЧНЫЙ МАТЕРИАЛ К ЗАЧЕТАМ ПО ПДД

Оговоримся сразу, что центрального (осевого) растяжения в реальных конструкциях не встречается. Причины: неоднородность бетона, неточности расположения арматуры по поперечному сечению и др.

Но на центральное растяжение условно рассчитывают затяжки и подвески арок, нижние пояса и нисходящие раскосы ферм, стенки круглых в плане резервуаров для жидкостей при отношении радиуса к толщине стенки 10 и более и некоторые другие конструктивные элементы (рис. 12.1).

Рисунок 12.1 – Центрально растянутые элементы: 1 – затяжка арки; 2 – нисходящие раскосы фермы; 3 – нижний пояс фермы; 4 – стенка круглого в плане резервуара

Стержневую рабочую арматуру соединяют по длине обычно с помощью сварки, стыки внахлёстку без сварки допускаются только в плитных и стеновых конструкциях.

Элементы, испытывающие совместное действие продольной растягивающей силы, приложенной в центре тяжести сечения, и изгибающего момента, работают на внецентренное растяжение. В условиях внецентренного растяжения находятся стенки резервуаров (бункеров), прямоугольных в плане, испытывающие внутреннее давление от содержимого, нижние пояса безраскосных ферм и некоторые другие элементы конструкций (рис. 12.2).

Рисунок 12.2 – Внецентренно растянутые элементы: а – стенка резервуара (бункера); б – нижний пояс безраскосной фермы.

При внецентренном растяжении различают два случая приложения продольной растягивающей силы N от внешней нагрузки: она может быть приложена за пределами расстояния z_s между равнодействующими усилий в арматуре A_s и A'_s (рис. 12.3а) и между равнодействующими усилий в арматуре A_s и A'_s (рис. 12.3б).

Рисунок 12.3 – Расчетные схемы внецентренно растянутых элементов при расположении продольной растягивающей N: а – за пределами расстояния между равнодействующими усилий в арматуре А_s и A’_s; б – между равнодействующими усилий в арматуре А_s и A’_s

Центрально растянутые элементы проектируют чаще всего квадратного поперечного сечения или прямоугольного с отношением сторон близким к единице, а внецентренно растянутые - прямоугольного сечения, вытянутыми в направлении действия изгибающего момента.

В центрально растянутых элементах рабочую продольную арматуру следует располагать симметрично относительно осей симметрии сечения. Диаметр стержней рекомендуется назначать от 6 до 28 мм. Целесообразно применять по возможности арматуру мелких диаметров, получая тем самым большее число стержней, что позволяет добиться более равномерного распределения напряжений в сечении и ограничить ширину раскрытия трещин. Такие элементы армируют пространственным (или плоским) арматурным каркасом сварным или вязаным. У всех поверхностей этих элементов, вблизи которых ставится продольная арматура, должна предусматриваться также поперечная арматура, охватывающая крайние продольные стержни. При этом расстояния между поперечными стержнями у каждой поверхности элемента должны быть не более 600 мм и не более удвоенной ширины грани элемента.

Внецентренно растянутые элементы снабжаются двойной продольной арматурой, расположенной по коротким сторонам сечения и соединённой между собой поперечными стержнями или хомутами, устанавливаемыми в соответствии с конструктивными требованиями норм. Коротко эти требования можно сформулировать так: внецентренно растянутые элементы, работающие по случаю 1, армируются продольными и поперечными стержнями аналогично изгибаемым элементам; внецентренно растянутые элементы, работающие по случаю 2, армируются подобно центрально растянутым элементам.

Для растянутых элементов с ненапрягаемой арматурой класса A-III и ниже применяют бетоны классов В15...В25.

Минимальное содержание арматуры в центрально растянутых элементах должно составлять 0,1% (устанавливается из условия предупреждения внезапного разрушения при раскрытии трещин); для внецентренно растянутых элементов, работающих по случаю 2, p_тin =p'_min = 0,05% . Для внецентренно растянутых элементов, работающих по случаю 1, площадь сечения продольной растянутой арматуры A_s должна составлять не менее 0,05% , а минимальное содержание арматуры A'_s не ограничивается.

2. Расчёт прочности центрально растянутых элементов

При постепенном возрастании растягивающего усилия до разруша­ющего центрально растянутый элемент проходит три следующие ха­рактерные стадии работы:

I— до появления трещин в бетоне, когда и σ_s < 30 МПа;

II— трещины появились, бетон уже не работает на растяжение, но напряжения в арматуре 30 МПа < σ_s < σ_у (предела текучести);

III— напряжения в арматуре достигают σ_у и элемент разру­шается. К моменту разрушения элемент оказывается рассечённым сквозными трещинами.

Рисунок 12.4 – Расчетная схема центрально растянутого элемента

В основу расчёта прочности положена стадия III напряжённо-деформированного состояния при осевом растяжении, т. е. счита­ется, что растягивающее усилие N от внешней нагрузки целиком должно быть воспринято арматурой, а бетон на растяжение не ра­ботает и лишь играет роль защитной оболочки. Расчётная схема центрально растянутого элемента представлена на рис. 12.4, для ко­торой можно составить одно уравнение равновесия

где A_s — площадь поперечного сечения всей продольной арматуры

3. Расчёт прочности элементов прямоугольного сечения, внецентренно растянутых в плоскости симметрии

При расчёте в зависимости от величины эксцентриситета e₀ = M/N различают два случая внецентренного растяжения.

Случай 1 — растягивающее усилие от внешней нагрузки находит­ся за пределами расстояния z_s между равнодействующими усилий в арматуре A_s и A'_s (e^’ > z_s). Здесь часть сечения, более удалённая от силы N, сжата (рис. 12.3а).

В основу расчёта положены те же предпосылки, которые исполь­зовались при расчёте нормальных сечений изгибаемых непереармированных элементов с двойной арматурой.

Условие прочности получают из сопоставления изгибающего мо­мента от внешней нагрузки и суммы моментов внутренних сил, взя­тых относительно центра тяжести растянутой арматуры A_s

(*)

Высоту сжатой зоны находим из второго уравнения равновесия

(**)

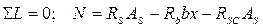Высота сжатой зоны ограничивается двойным неравенством

где ξ_R граничное значение высоты сжатой зоны

Если найденное из (**) значение х > ξ_Rh₀, то в правую часть неравенства (*) подставляют х = ξ_Rh₀.

Подбор сечений

Размеры бетонного сечения элемента, как правило, бывают из­вестны.

Наиболее экономичное армирование A_S+A'_S получается при х = х_R = ξ_Rh₀ тогда α_m = α_R = ξ_R (1 - 0,5ξ_R). Перепишем (*) и (**), введя в них значения х_R и α_m, по

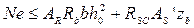
получим

При принятом (или заданном) A'_s с учётом того, что х = ξh₀ и коэффициент α_m определяется по формуле α_m = ξ(1 - 0,5ξ), выра­жения (*) и (**) перепишутся так

(***)

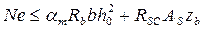Определяем А_s следующим образом: из (5.2б) находим

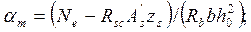
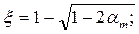
Если условие (***) не выполняется и х < 2а', то полагая х = 2а', определяем A_s из уравнения

ΣM_A’s= 0; Ne' = R_sA_sz_s, откуда А_s = Ne'/(R_sz_s).

Случай 2 — растягивающее усилие от внешней нагрузки нахо­дится в пределах расстояния z_s между равнодействующими усилий в арматуре A_s и A’_s (e^’ ≤z_s). При малых эксцентриситетах трещины, как и при центральном растяжении, насквозь пронизывают бетонное сечение элемента уже при относительно небольшой нагрузке. После образования трещин в элементе на растяжение продолжает рабо­тать только арматура. Условия прочности здесь получают, составив уравнения моментов относительно центров тяжести арматуры A_s и А'_s, в соответствии с расчётной схемой, показанной на рис. 12.3б:

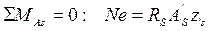
Откуда A'_s ≥ Nе/(R_sz_s).

откуда A_s≥Ne'/(R_sz_s).

Эти формулы непосредственно используют для подбора арматуры и для проверки несущей способности элементов.

РАЗДАТОЧНЫЙ МАТЕРИАЛ К ЗАЧЕТАМ ПО ПДД