Раздаточный материал по курсу

14.Ряд Фур’є для парних і непарних функцій. Дискретний спектр функції. Ряд Фур’є в комплексній формі. Комплексний дискретний спектр функції.

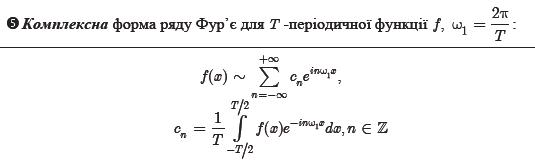
15.Інтеграл Фур’є ,(простий та подвійний). Теорема про збіжність Інтегралу Фур’є. Інтеграл Фур’є парних і непарних функцій. Синус і косинус перетворення Фур’є. Спектр функції.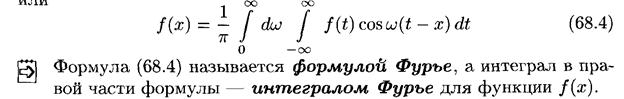

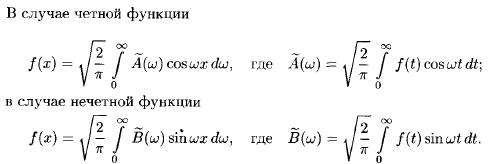
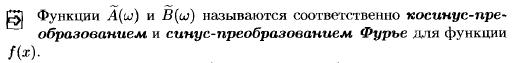
17. Похідна ФКЗ: означення. Умови Коші-Рімана. Приклад.

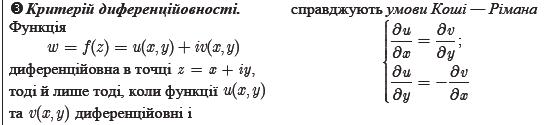
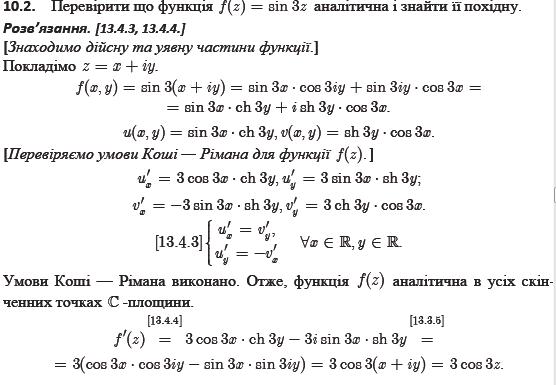
18. Означення аналітичної функції в точці та на множині. Приклад. Гармонічні функції та їх зв’язок з аналітичними. Відновлення аналітичної функції по її дійсній частині.

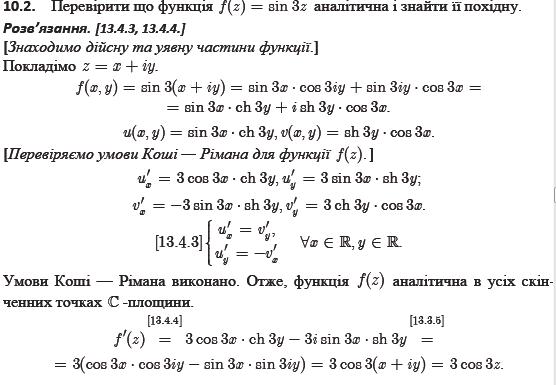
19. Означення інтеграла в комплексній області та його обчислення. Властивості цього інтеграла (довести теорему про оцінку модуля).

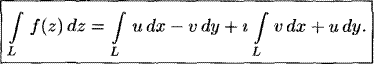
20.Інтегральна теорема Коші. Наслідок для неоднозв’язних областей та системи контурів. Обчислення інтеграла ∮ , де n-ціле число , Г-довільний контур.

21.Первісна аналітичної функції. Теорема існування та формула Ньютона-Лейбніца.

22.Інтегральна формула Коші. Інтеграл типу Коші та його аналітичність.

23. Теорема про перехід до границі під знаком інтеграла. Теорема Вейерштрасса про послідовності аналітичних функцій. Наслідок для рядів.

Раздаточный материал по курсу

ПСИХОЛОГИЧЕСКАЯ ДИАГНОСТИКА РАЗВИТИЯ
МЛАДШИХ ШКОЛЬНИКОВ
(С ПРАКТИКУМОМ)

Направление подготовки:
050400.62 - Психолого-педагогическое образование
Квалификация (степень) выпускника - бакалавр
Профиль «Психолог образования»

Автор и составитель программы:

Валентина Михайловна Кабаева,

кандидат психологических наук, доцент кафедры педагогической психологии МГППУ

Москва . 2012
Оглавление