Знайти площу частини площини , вирізаної координатними площинами.

в) ;

Обчислити потік векторного поля через зовнішню сторону замкненої поверхні . ; .

г)1/3;

Знайти потік векторного поля через повну поверхню конуса застосувавши формулу Остроградського.

а) ;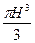

Знайти площу частини площини , вирізаної координатними площинами.

в) ;

Задано векторне поле і площина ( ), яка разом з координатними площинами утворює піраміду V. Нехай – основа піраміди, яка належить площині ( ); – контур, який обмежує , – зовнішня нормаль до . Обчислити циркуляцію векторного поля вздовж замкненого контура , застосувавши формулу Стокса до контура і обмеженої ним поверхні з нормаллю .

Г) --6

Задано векторне поле і площина ( ), яка разом з координатними площинами утворює піраміду V. Нехай – основа піраміди, яка належить площині ( ); L – контур, який обмежує , – зовнішня нормаль до . Обчислити циркуляцію векторного поля вздовж замкненого контура , застосувавши формулу Стокса до контура і обмеженої ним поверхні з нормаллю .

В)1