Свойства определенного интеграла. 4) Если f(x) £ j(x) на отрезке [a, b] a < b, то

1)

2)

3)

4) Если f(x) £ j(x) на отрезке [a, b] a < b, то

5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

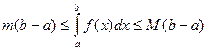
6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что

Доказательство: В соответствии со свойством 5:

т.к. функция f(x) непрерывна на отрезке [a, b], то она принимает на этом отрезке все значения от m до М. Другими словами, существует такое число eÎ [a, b], что если

и m = f(e), а a £ e £ b, тогда . Теорема доказана.

7) Для произвольных чисел a, b, c справедливо равенство:

Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.

8)

Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке [a, b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что