
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Александр Лоуэн
Лекция №1
Тема лекции: Предмет курса; задачи курса; формы отчетности; литература.
Понятие машины, узла, детали. Классификация деталей и сборочных единиц. Критерии работоспособности деталей машин.
Дисциплина «Детали машин и основы конструирования» изучает основные детали, используемые при конструировании машин, сборочные единицы и узлы, используемые в машиностроении.
Задачей курса является овладение студентом терминологией, получение навыков вычерчивания эскизов, чертежей и расчетных схем отдельных деталей и узлов, выработка умения обосновать причину выбора конкретной детали или конструкции узла и умения провести с помощью справочной литературы выбор материала, выполнение проектных и проверочных расчетов.
Курс включает в себя лекционный материал, семинарские и лабораторные занятия, расчетно-графические задания, экзамен, курсовой проект, защиту курсового проекта и зачет.
Для овладения материалом курса рекомендуется дополнительная литература, которая поможет уяснить и расширить понимание отдельных вопросов лекционного курса, а также будет использована в качестве справочной при работе над расчетно-графическими заданиями и курсовым проектом.
1. Иванов М.Н. Детали машин. – М.: Высшая школа, 1991. – 383 с.
2. Ким В.С., Самойлов В.А., Торубаров Н.Н. Конструирование и расчет механизмов и деталей машин химических и нефтеперерабатывающих производств. – М.: КолосС, 2007. – 440 с.
3. Решетов Д.Н. Детали машин. – М.: Машиностроение, 1989. – 496 с.
4. Анурьев В.И. Справочник конструктора –машиностроителя: В 3-х т. – М.: Машиностроение. 2003.
5. Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. – М.: Академия, 2009. – 496 с.
6. Самойлов В.А., Талачев В.С., Порчхидзе Г.Д. Детали машин. Основы конструирования. Курсовой проект. – М.: МГУИЭ, 2006. – 92 с.
7. Целиковская А.И., Егоров Ю.В. Расчет зубчатых передач. Практикум. – М.: МГУИЭ, 2006. – 116 с.
Машиностроение – фундамент экономики современного государства; авиация, транспорт, сельское хозяйство, текстильная промышленность, пищевая промышленность и т.д. существуют на основе машин и аппаратов. Машина – устройство, предназначенное для выполнения конкретного вида механических операций без изменения физического, химического или агрегатного состояния объекта. Примерами могут служить: эскалатор метро, предназначенный для механической операции – перемещения пассажиров; трактор, предназначенный для транспортировки плуга или прицепа; токарный или фрезерный станок, предназначенные для срезания металла с поверхности заготовки и т. д. Аппарат – устройство, предназначенное для изменения агрегатного, физического или химического состояния объекта. Примерами могут служить кофемолка, изменяющая агрегатное состояние кофейных зерен путем их измельчения; чайник, изменяющий физическое состояние воды путем её нагрева; химический реактор, в котором смесь исходных компонентов, после нагрева и приложения давления синтезирует продукт с новым химическим составом. Данный курс рассматривает составные части машин, способы их соединения и методы расчета отдельных деталей и узлов. Однако, этот курс полностью применим и к вопросам конструирования и механического расчета составных частей аппаратов.
Для описания структуры машины используются три термина – деталь, сборочная единица и узел. Деталь – часть машины, выполненная из монолита какого-либо материала без применения сборочных операций, таких как сварка, пайка, клепка. Примерами деталей могут служить: 1-болт выточенный на токарном и фрезерном станках из стального прутка круглого профиля; 2- шайба; 3- вал.

1 3 2 3
Сборочная единица – комбинация деталей, образующая функциональный узел. Примером может служить подшипник качения, состоящий из шариков (или роликов), пары колец с дорожками для размещения шариков.
Узел – комбинация деталей и сборочных единиц, часто для выполнения конкретной функции. Примером может служить узел - двигатель автомобиля или узел - коробка передач; каждый из этих узлов выполняет специальную функцию. Двигатель служит источником движения; коробка передач изменяет параметры вращения двигателя.
Детали и узлы подразделяются на типовые (стандартные) и специальные. Типовые производятся на специализированных заводах специальным ассортиментом - типорядом. Например болты выпускаются рядом с внешними диаметрами резьбовой части . . . 8мм.; 10мм.; 12мм.; 16мм.; . . . и дополнительно для каждого диаметра предусматривается ряд длин. Поэтому конструктор может выбрать готовый болт нужного диаметра и длины. Это исключает необходимость специального изготовления такого болта, снижает время проектирования и удешевляет конструкцию. Кроме того деталь изготовленная на специализированном заводе имеет гарантированно высокое качество и низкую стоимость по сравнению с изготовленной индивидуально. Такие детали и узлы используются без изменения во всех машинах и аппаратах. Например, один и тот же подшипник может быть использован и в автомобиле и в катере и в кофемолке. Специальные детали и узлы предназначены только для конкретной машины. Например, гребной винт катера не может быть использован ни для какой другой машины.
Классификация узлов и деталей машин.
1.Соединения. (Служат для соединения деталей и узлов)
1.1Резьбовые соединения.
1.2Сварные соединения.
1.3Шпоночные и шлицевые соединения
1.4Прессовыесоединения
1.5Клеммовые соединения
1.6Заклёпочные соединения
2.Валы и оси. (Служат для размещения на них деталей и узлов, передачи крутящего момента и восприятия нагрузок)
3.Передачи. (Служат для преобразования параметров вращения: частоты, крутящего момента, характера и направления вращения)
3.1Зубчатые передачи
3.2Червячные передачи
3.3Ременные передачи
3.4Передачи катками
3.5 Цепные передачи
3.6Передачи винт-гайка
4.Подшипники. (Обслуживают вращение валов и осей, уменьшая трение в опорах)
5.Муфты. (Соединяют концы валов и осей с передачей вращения и крутящего момента и могут выполнять специальные функции).
Критерии работоспособности деталей машин.
Работоспособность – свойство детали, узла или машины выполнять свои функции в течение расчетного срока без отказов (нарушение работоспособности).
1. Прочность.
2. Жесткость.
3. Виброустойчивость.
4. Износостойкость.
5. Тепло и хим-стойкость.
6. Надежность.
Прочность.
Прочность – способность детали сохранять работоспособность при воздействии нагрузок в течение расчетного срока. Различают два вида прочности. Первое - статическая прочность. Второе – выносливость (усталостная прочность или циклическая прочность).
Статическая прочность – это прочность при действии постоянных во времени нагрузок.
F
t
Разрушение или потеря работоспособности детали при статическом нагружении происходит либо путем её поломки, либо от пластических деформаций. В этом случае прочность детали оценивают сравнением действующих напряжений с опасным напряжением. Величину опасного напряжения для детали получают в процессе испытания материала, из которого эта деталь изготовлена. В качестве примера можно рассмотреть диаграмму растяжения образца.

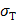
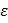
В процессе испытания фиксируют текущую зависимость величины напряжения 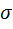 от величины деформации
от величины деформации 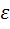 . Здесь величина напряжения и деформации:
. Здесь величина напряжения и деформации:
 ;
; 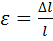 .
.
F – величина усилия прикладываемого к образцу;
A- Площадь поперечного сечения образца;
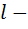 первоначальная длина образца;
первоначальная длина образца;
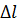 - величина удлинения образца под действием силы F.
- величина удлинения образца под действием силы F.
 испытания отмечается величина
испытания отмечается величина  , напряжения при котором начинается интенсивный рост деформации без увеличения напряжения. Эта величина называется предел текучести материала и при ней начинается потеря работоспособности детали из-за пластической деформации. Поэтому, за опасное напряжении принимается эта величина.
, напряжения при котором начинается интенсивный рост деформации без увеличения напряжения. Эта величина называется предел текучести материала и при ней начинается потеря работоспособности детали из-за пластической деформации. Поэтому, за опасное напряжении принимается эта величина.
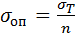 .
.
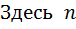 − коэффициент запаса, принимаемый для предотвращения достижения деталью при эксплуатации опасного напряжения, поскольку прочностные свойства материалов не всегда точно соответствуют величинам, определенным в процессе экспериментов.
− коэффициент запаса, принимаемый для предотвращения достижения деталью при эксплуатации опасного напряжения, поскольку прочностные свойства материалов не всегда точно соответствуют величинам, определенным в процессе экспериментов.
 − это прочность материала при действии циклических нагрузок. Циклические нагрузки в общем случае имеют такой характер:
− это прочность материала при действии циклических нагрузок. Циклические нагрузки в общем случае имеют такой характер:


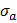
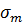

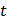
Здесь 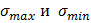 максимальная и минимальная величины напряжений возникающих в детали.
максимальная и минимальная величины напряжений возникающих в детали.
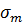 - среднее напряжения цикла равное полусумме максимального и минимального значений.
- среднее напряжения цикла равное полусумме максимального и минимального значений.
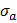 - амплитуда изменения напряжения, измеряемая от уровня среднего напряжения.
- амплитуда изменения напряжения, измеряемая от уровня среднего напряжения.
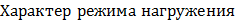 индексируется величиной – r , называемой параметром ассиметрии цикла нагружения. Оно определяется величиной:
индексируется величиной – r , называемой параметром ассиметрии цикла нагружения. Оно определяется величиной:
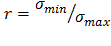
Выносливость характеризуется величиной коэффициента запаса:
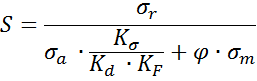
Здесь:
 - экспериментальная величина предела выносливости материала детали, полученная при испытаниях материала с режимом нагружения имеющим параметр ассиметрии – r.
- экспериментальная величина предела выносливости материала детали, полученная при испытаниях материала с режимом нагружения имеющим параметр ассиметрии – r.
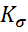 – коэффициент влияния на выносливость концентратора напряжений в рассчитываемом сечении. Концентратором является любое нарушения правильной формы сечения детали – такое как отверстия, резьба, канавки и т.д.
– коэффициент влияния на выносливость концентратора напряжений в рассчитываемом сечении. Концентратором является любое нарушения правильной формы сечения детали – такое как отверстия, резьба, канавки и т.д.
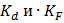 – коэффициенты влияния на выносливость диаметра сечения и шероховатости его поверхности.
– коэффициенты влияния на выносливость диаметра сечения и шероховатости его поверхности.
 – коэффициент влияния на выносливость величины среднего напряжения цикла нагружения.
– коэффициент влияния на выносливость величины среднего напряжения цикла нагружения.
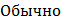 выносливость считается достаточной, если величина коэффициента запаса не менее 1,5.
выносливость считается достаточной, если величина коэффициента запаса не менее 1,5.
Жесткость – способность детали сохранять величину деформации в пределах, не нарушающих её работоспособность. Жесткость характеризуется тремя критериями, которые можно проиллюстрировать на примере детали вал – деталь цилиндрической формы:
Под действием приложенной силы вал прогнулся; величина прогиба является первым критерием жесткости. Второй критерий угол поворота сечения вала или его оси. Третий критерий угол закручивания от приложенного крутящего момента.
Виброустойчивость – способность детали, которая вращается или подвержена динамическому нагружению, противостоять возникновению вибрации и резонансных явлений. Это достигается введением ограничений на величину деформации детали, хорошей балансировкой и работой с частотами вращения меньшими или большими частот вызывающих возникновение резонансных колебаний.
Износостойкость – способность детали сохранять размеры частей подверженных в процессе работы трению в пределах допуска на износ в течение расчетного срока эксплуатации. Это обеспечивается использованием материалов стойких к износу, использованием поверхностного упрочнения, шлифованием и полировкой поверхностей, а также использованием смазки и специальных покрытий.
Тепло и химстойкость - способность детали или машины сохранять работоспособность при повышенных температурах и в агрессивных средах. Обеспечивается использованием специальных сортов материалов для изготовления деталей (например, жаростойких и коррозионностойких сталей и сплавов), а также применением защитных покрытий.
Надежность - гарантированная способность детали и машины сохранять работоспособность в течение расчетного срока эксплуатации. Обеспечивается повышением надежности каждой детали в машине, по возможности снижением их количества при проектировании машины и строгим выполнением регламента технического обслуживания.
Контрольные вопросы по теме лекции.
1. В чем различие между машиной и аппаратом?
2. Из чего состоит машина и узел?
3. Что такое типовая деталь и деталь специальная?
4. Перечислите критерии работоспособности деталей машин.
5. Чем отличается прочность детали от выносливости?
6. Что такое предел текучести материала?
7. Какая величина характеризует выносливость детали?.
8. Что такое концентратор напряжений? Дайте примеры.
9. Что такое жесткость детали? Как повысить жесткость
10. Что такое виброустойчивость?
11. Что такое износостойкость, способы её увеличения?
12. Что такое тепло и химстойкость, чем они обеспечиваются?
13. Что такое надежность? Способы её обеспечения.
Лекция №2
Тема: Механические передачи; сравнительная характеристика.
Если проанализировать кинематические характеристики электродвигателей и рабочих органов рассмотренных машин, то можно сделать общее заключение, что частота вращения электродвигателя во много раз больше чем частота вращения рабочего органа. Так частота вращения шнека экструдера или литьевой машины составляет величину порядка 10-100 оборотов в минуту, а частота вращения электродвигателя привода таких машин равна 600-1000 оборотам в минуту. Поэтому любая из рассмотренных машин обязательно имеет устройство, называемое передачей.
Механическими передачами называются устройства, предназначенные для передачи вращения от одного устройства к другому с изменением частоты вращения, крутящего момента, направления и характера вращения. Основными видами механических передач являются следующие:
1. Зубчатые передачи.
2. Червячные передачи.
3. Ременные передачи.
4. Передачи катками.
5. Цепные передачи.
6. Передачи винт-гайка.
Зубчатые передачи.
Зубчатые передачи образуются несколькими зубчатыми колесами (как минимум двумя) и относятся к передачам зацеплением.
 а) б)
а) б)
Рис.а) -внешний вид передачи; б)- её условное изображение в двух проекциях- слева – вид спереди; справа – вид сбоку.
Меньшее по диаметру из пары зубчатое колесо называется шестерня, все её параметры имеют индекс -1: z1 – число зубьев шестерни; n1 – частота вращения шестерни; d1 - делительный диаметр.
Большее по диаметру зубчатое колесо из пары называется колесо, и все его параметры имеют индекс – 2. z2 -число зубьев; n2-частота вращения; d2-диаметр делительной окружности.
Термин зубчатое колесо является общим.
Основные параметры зубчатой передачи:
1. Отношение чисел зубьев, диаметров или обратное отношение частот вращения называется передаточным числом.
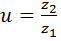 =
= 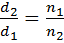 .
.
Передаточное число показывает, во сколько раз изменяется частота вращения ведомого зубчатого колеса при передаче вращения от ведущего зубчатого колеса. Эта величина для зубчатых передач может находиться в интервале от 1 до 20, но обычно используется интервал от 1 до 8.
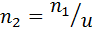
2. Отношение мощности снимаемой с ведомого зубчатого колеса к мощности, подводимой к ведущему, называется коэффициентом полезного действия – к.п.д.
η= 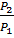 .
.
Величина «единица минус к.п.д.» определяет величину механических потерь мощности в передаче. Для зубчатых передач она составляет примерно 3%. Это самое высокое значение к.п.д. из всех типов передач 0,97.
3. Уменьшение частоты вращения при передаче от шестерни к колесу вызывает увеличение крутящего момента снимаемого с колеса в передаточное число раз, но с учетом механических потерь -η:
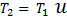 η.
η.
4. Зубчатые передачи имеют минимальный габарит (размер) по сравнению с остальными передачами.
5. Зубчатые передачи имеют максимальный ресурс (срок службы) по сравнению с остальными передачами; порядка нескольких десятков тысяч часов.
6. Зубчатые передачи имеют невысокий уровень шумности, достаточно высокие плавность работы и постоянство передаточного числа.
7. Зубчатые передачи могут передавать большие мощности (до нескольких сотен тысяч киловатт).
Зубчатые колеса могут иметь различный тип зуба.
1 2 3
1 – прямозубое зубчатое колесо – используется для тихоходных передач;
2 – косозубое зубчатое колесо – используется в быстроходных передачах;
3 – шевронное зубчатое колесо – используется в тяжело нагруженных передачах.
Червячные передачи
 а) б)
а) б)
На рис. а) – внешний вид червячной передачи; б) – условное изображение
Червячная передача состоит из червяка -1 и червячного колеса – 2. Червяк представляет собой винт, а червячное колесо (колесо) является аналогом косозубого зубчатого колеса.
Передача передает вращение между взаимно перпендикулярными осями. Она работает за счет сил трения между витками червяка и зубьями колеса; отсюда более низкий к.п.д. чем у зубчатой передачи – его нижнее значение может достигать 0,6. Также высокие требования к качеству смазки и к материалам для пары червяк – колесо. Пара материалов должна иметь низкий коэффициент трения. Червяк представляет собой винт, и он может иметь разное значение заходности – z1. Заходность это число винтовых линий червяка. Она может иметь значение 1, 2 и 4.
1. 2.
На схеме 1 заходность равна 1 – одна винтовая линия. На схеме 2 заходность равна 2 – две винтовые линии (для наглядности вторая винтовая линия изображена с большей толщиной). Число зубьев червячного колеса не рекомендуется принимать меньшим 28 из-за сложности формы зуба. Поэтому передаточное число червячной передачи:
 .
.
 z2 - число зубьев колеса;
z2 - число зубьев колеса;
n1 и n2 - числа оборотов червяка и колеса соответственно.
Так как число зубьев колеса не может быть меньшим 28, а максимальная заходность червяка 4, то минимальное передаточное число – 7. Зато максимальное может доходить до 1000.
Работа червячной передачи отличается высокой плавностью и бесшумностью. Из-за низкого к.п.д. применение ограничивается значениями передаваемой мощности до 200 кВт.
Отличительным свойством является эффект самоторможения – вращение может передаваться от червяка к колесу; передача в обратном направлении не возможна.
Червяк может иметь различную форму и профиль витков.
а б в
а – цилиндрический червяк; б – конический червяк; в – глобоидный червяк
Глобоидный червяк может работать с большим числом зубьев колеса и поэтому более высокая нагрузочная способность.
n
а а
n
Профиль витков червяка в сечении а-а может быть (а) прямолинейным, это Архимедов червяк (обозначение - ZA); в торцевом сечении n-n профиль - архимедова спираль. Червяки с таким профилем легко вытачиваются на токарных станках резцом, но трудно шлифуются. Поэтому используются в тихоходных и малонагруженных передачах.
а б
Конволютные червяки- ZN, профиль витка б в сечении n-n – эвольвента. Эвольвентные червяки – аналог зубчатых колёс с большим углом наклона зуба ZI.
Ременные передачи
Состоит из двух цилиндров (шкивов) 1 и 2 и охватывающего их ремня -3. Работа передачи осуществляется за счет сил трения между ремнем и шкивами, возникающих при раздвигании шкивов, создающего предварительное натяжение ремня. Передача может иметь передаточное число в интервале от 1 до 10, но обычно от 2 до 5. Габарит передачи (размер) значительно больше, чем у зубчатых и червячных передач. Передача может осуществляться на расстояние до 15 метров. Ременная передача обладает свойством самопредохранения, т.е. при перегрузках происходит проскальзывание ремня по малому шкиву без поломки передачи. Из-за проскальзывания передаточное число непостоянно. Ресурс (срок службы) невелик – порядка 2000 – 3000 часов из-за растяжения и износа ремня; так как ремень изготовлен из материалов с низкой прочностью и при работе подвержен действию сил трения. Однако передача достаточно дешевая. Нагрузочная способность невелика.
Передачи катками
Катки – тела вращения (цилиндры -а или конусы -б) с гладкой поверхностью, имеющей высокий коэффициент трения. Передача состоит из пары таких тел прижатых друг к другу значительной силой.
а F F б
F F
Передача вращения происходит за счет сил трения поверхностей катков. Передаточное число определяется также как и для зубчатых передач – отношением диаметров или частот вращения. Из-за относительного проскальзывания катков передаточное число непостоянно и зависит от величины передаваемого крутящего момента. Передаваемые мощности и долговечность (ресурс) передачи невелики. Но на основе катков можно сконструировать передачи с плавно изменяющимся передаточным числом.
Изменяя расстояние малого ролика от оси большого можно плавно менять частоту вращения большого.
Цепные передачи
| б |
а
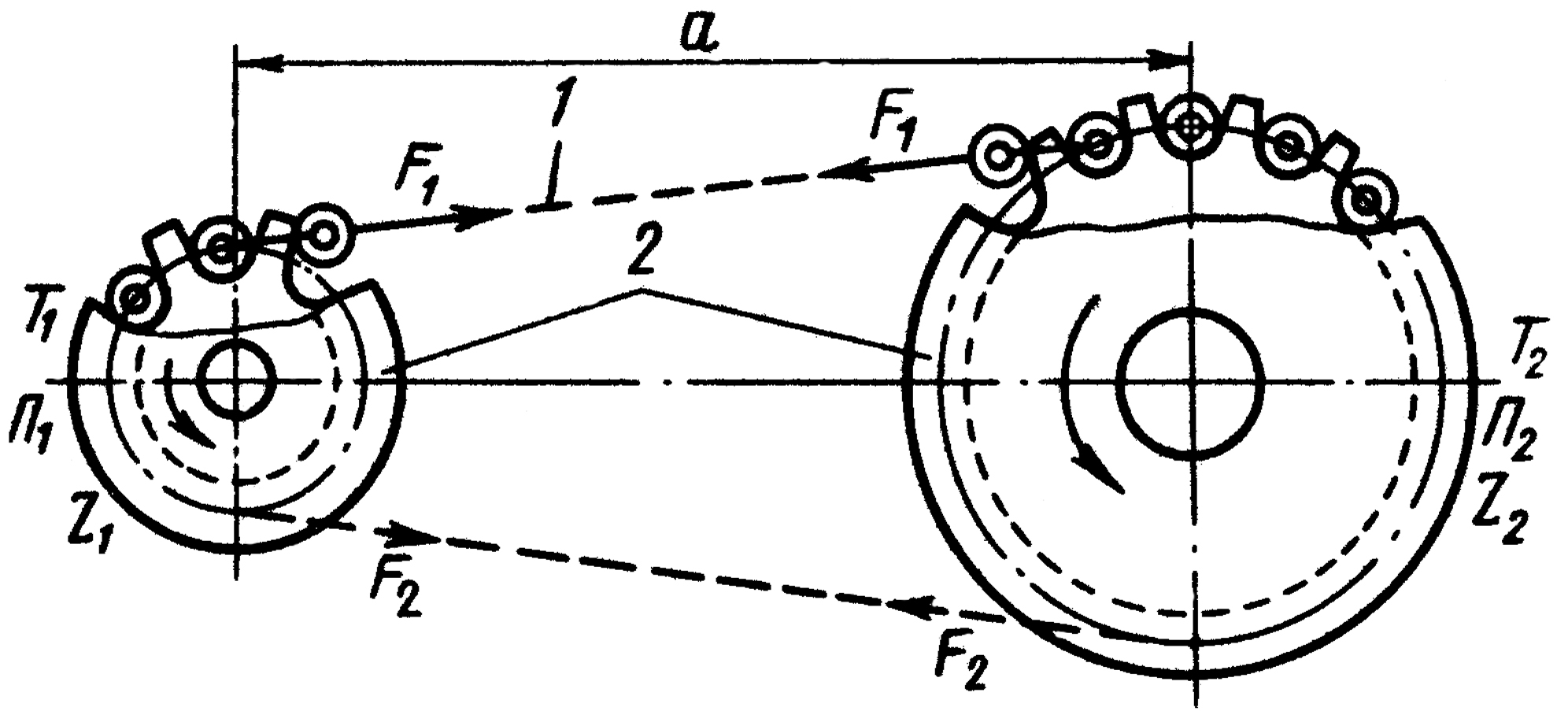
а – вид на цепную передачу сбоку; б – условное изображение цепной передачи в двух проекциях. Передача состоит из двух зубчатых деталей – звездочек 1 и 2 и цепи -3. Передача является тихоходной, так как из-за того, что цепь может изгибаться только в шарнирах, её линейная скорость непостоянна и возникает скорость поперечная линии цепи, приводящая к её колебанию. Цепная передача может передавать крутящий момент на значительные расстояния и имеет постоянное передаточное число при меньших габаритах, чем ременная. Смазка передачи затруднена, поэтому имеет место износ шарниров, приводящий к вытяжке цепи и необходимости её натяжения. Передаточное число рекомендуется в интервале от 1 до 5. К.п.д. порядка 0,95.
Передача винт-гайка
Состоит из винта -1 и гайки – 2. Если гайку зафиксировать от возможности вращения и вращать винт, зафиксировав его от осевых перемещений, то гайка будет двигаться в осевом направлении. Если зафиксировать гайку от осевых перемещений, а винт от возможности вращения и вращать гайку, то винт будет перемещаться в осевом направлении. Такие передачи используются в винтовых домкратах, винтовых прессах, механизмах приборов и т.д.
Такая передача может иметь передаточное число, измеряемое условно зависимостью:
u= 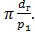
Здесь: 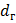 - наружный диаметр гайки;
- наружный диаметр гайки;
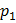 - ход винта (расстояние между одноименными точками соседних витков).
- ход винта (расстояние между одноименными точками соседних витков).
Определенное таким образом передаточное число может иметь величину до 1000. К.п.д. такой передачи в её простом конструктивном варианте очень низкий, порядка 0,2. Одним из ограничений передачи является её ограниченное действие, определяемое длиной винта. При достижении гайкой конца винта передача прекращается.
Контрольные вопросы
1. Перечислите виды механических передач.
2. Объясните назначение передач.
3. Изобразите эскизы передач.
4. Что такое коэффициент полезного действия передачи?
5. Какая передача имеет максимальный к.п.д. и какая минимальный?
6. Какая из передач может иметь передаточное число больше 100?
7. Что такое передаточное число передачи?
8. Если требуется передача с минимальными размерами, какой вид передачи следует выбрать?
9. Если требуется передача с передаточным числом 4, какую передачу нельзя использовать?
10. Какая из передач имеет свойство самопредохранения и что это такое?
11. Какая из передач имеет самое высокое постоянство передаточного числа и плавность работы?
12. Какая из передач более всего подходит для использования в домкратах?
13. Какая из передач может передавать самую большую мощность?
Лекция №3
Тема: Зубчатые цилиндрические передачи. Основы геометрии.
| Рис. 3.1 |
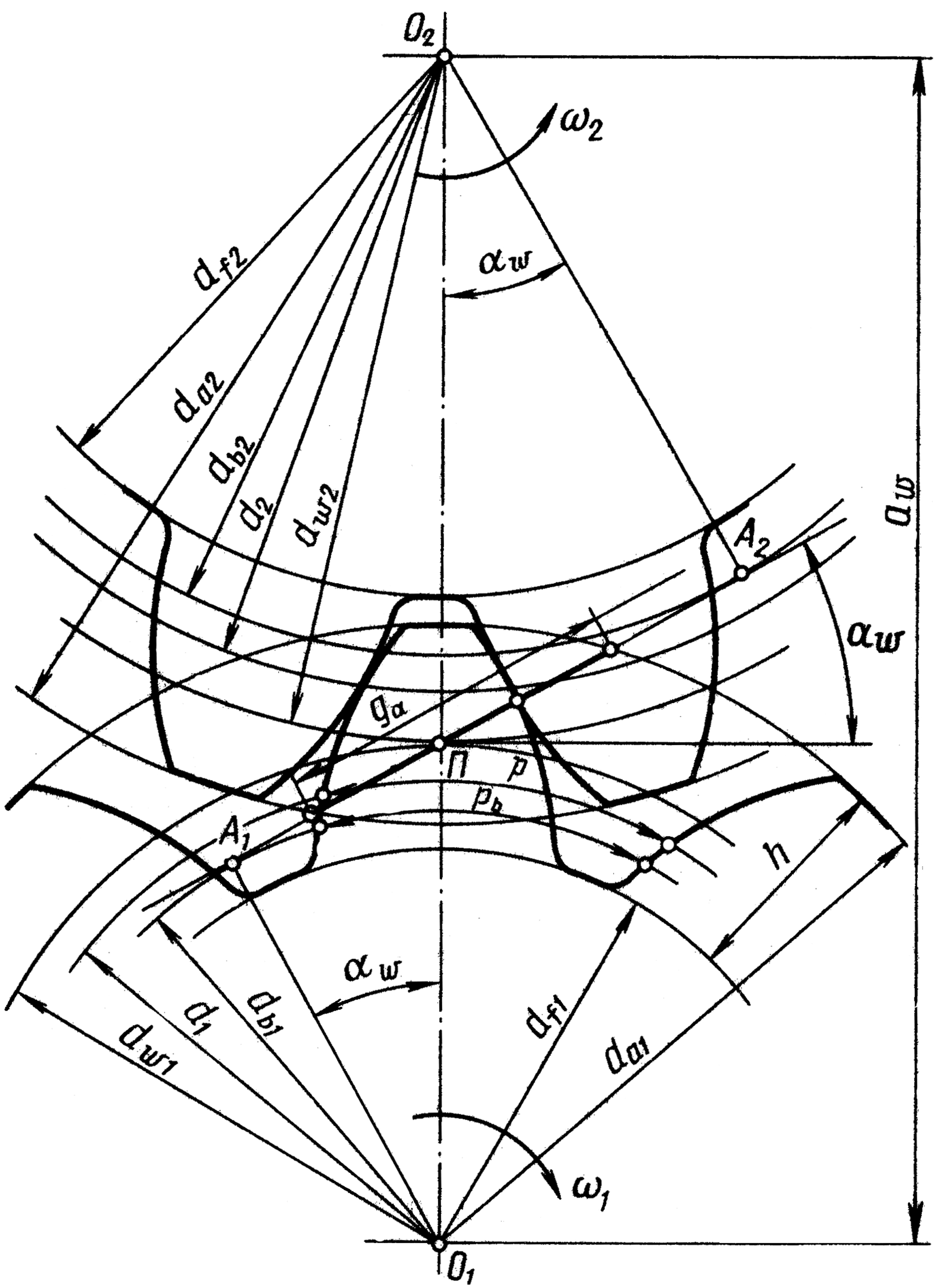
Схема соответствует виду на передачу со стороны её торца. Представлены два зубчатых цилиндрических колеса: внизу часть шестерни с центром в точке О1, а сверху часть колеса с центром в точке О2. Через эти точки проходят оси зубчатых колес, они перпендикулярны плоскости чертежа. Толстыми линиями изображены зубчатые колеса, а тонкими геометрические её параметры.
На вертикальной оси находится точка – «П» полюс зацепления зубчатых колес; в этой точке происходит контакт начальных цилиндров, диаметры которых обозначены как:

индекс 1 соответствует шестерне – меньшему по диаметру зубчатому колесу из пары;
индекс 2 – колесу большему по диаметру зубчатому колесу из пары. Эти цилиндры при вращении зубчатых колес обкатываются друг по другу без проскальзывания и поэтому отношение этих диаметров равно передаточному числу:
и = 
Полусумма этих диаметров равна межосевому расстоянию передачи (расстоянию между центрами зубчатых колес).
аω=(  )/2
)/2
Через полюс П под углом α к горизонтальной оси проходит линия зацепления А1 – А2, по которой движутся все точки контакта зубьев шестерни и колеса при их вращении. Вдоль этой линии направлены силы, действующие на зубчатые колеса. Величина угла α зависит от вида кривой образующей рабочую поверхность зуба. Наиболее удобной с точки зрения кинематики передачи является кривая – эвольвента. Она обеспечивает работу зубьев практически без скольжения их поверхностей друг по другу. Кроме эвольвенты могут быть использованы как образующие рабочую поверхность зуба дуга окружности и циклоида. В дальнейшем рассматриваются только эвольвентные зубчатые передачи. Отрезки О1 – А1 и О2 - А2 перпендикуляры к линии зацепления и они являются радиусами основных окружностей зубчатых колес.
 и
и 
На этих окружностях располагаются основания зубьев.
На схеме обозначены ещё два диаметра:
d1 и d2
Это диаметры делительных окружностей; по ним обкатывается инструмент при нарезании зубьев. При нарезании зубчатых колес без коррегирования диаметры делительный и основной равны.
Коррегированием называется процесс смещения инструмента используемого для нарезания зубьев в направлении центра колеса или наоборот. Это позволяет изменить профиль зуба, сделав его толще у основания, повысив прочность.
Если измерить расстояние между одноименными точками двух соседних зубьев по дуге окружности делительного диаметра, то получим величину называемую – шаг зуба
р
Для освоения основных геометрических параметров передачи целесообразно рассматривать её в прямозубом варианте и без применения коррегирования зубьев.
Если умножить шаг на число зубьев колеса, то получим длину делительной окружности, равную также произведению делительного диаметра на число π. Таким образом:
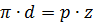 или
или
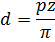
В этой зависимости отношение 
заменяют обозначением m – модуль передачи. Это её основная геометрическая стандартная характеристика. Она может назначаться в интервале от 0,05 до 100 мм. И с условием сделанных допущений можно записать выражения для основных геометрических параметров передачи.
| Параметр | Шестерня | колесо |
| Диаметр делительной окружности Диаметр окружности вершин зубьев Диаметр основной окружности Диаметр окружности впадин зубьев Ширина зубчатого венца Межосевое расстояние передачи Коэффициент радиального зазора Коэффициент ширины зубчатого венца |  d
d  d
d 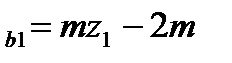

|  d
d  d
d 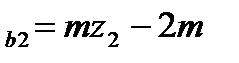 d
d 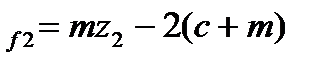
|
b=  
 =0,5(d1 + d2)
c=0,25m =0,5(d1 + d2)
c=0,25m
 =0,1 ¸ 1 =0,1 ¸ 1
|
При постоянных величинах аω, передаточного числа и, следовательно делительного диаметра, величина выбранного модуля будет влиять на размеры и число зубьев колес.
Большой модуль образует широкий и высокий зуб передачи и малое их число, что повышает прочность, но ухудшает кинематику. Маленький модуль дает маленький менее прочный зуб, но улучшает кинематику.
На схеме буквой h обозначена высота зуба. Высота состоит из вершины зуба (головки) и ножки. Вершина расположена между окружностями делительных диаметров:
d1 и d2
и окружностями вершин зубьев (внешние диаметры зубчатых колес):
dа1 и dа2
Ножка зуба расположена между окружностями делительных диаметров и окружностями впадин зубьев:
df1 и df2
Окружности впадин зубьев имеют меньший диаметр чем окружности оснований зубьев 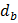 . Это принимается для того, чтобы при вращении вершины зубьев одного колеса не касались впадин зубьев другого колеса. Для этой цели ножка зуба увеличивается на величину 0,25 m. На этом участке поверхность зуба описывается не эвольвентой, а дугой окружности и контакта с другим зубом нет.
. Это принимается для того, чтобы при вращении вершины зубьев одного колеса не касались впадин зубьев другого колеса. Для этой цели ножка зуба увеличивается на величину 0,25 m. На этом участке поверхность зуба описывается не эвольвентой, а дугой окружности и контакта с другим зубом нет.
Окружности с диаметрами dа1 и dа2 отсекают на линии зацепления отрезок N1 – N2, на котором происходит фактический контакт зубьев. Это длина активной линии зацепления обозначаемая – gα. Эта линия является касательной к основным окружностям зубчатых колес и при качении по ним образует эвольвентные поверхности зубьев. Поэтому вводится шаг зуба по окружностям основного диаметра рb Отношение величины gα к шагу рb является коэффициентом торцевого перекрытия:
εα = gα/ рb
Эта величина показывает, сколько пар зубьев шестерни и колеса находятся в зацеплении одновременно (в среднем). Например, если коэффициент равен 1,5, то 50% времени в зацеплении находится один зуб шестерни и один зуб колеса; и 50% времени в зацеплении находятся 2 зуба шестерни и два зуба колеса, что снижает нагрузку на них и повышает их ресурс. Если коэффициент равен 1, то постоянно в зацеплении 1 зуб шестерни и один зуб колеса. А если коэффициент равен 0,9, то 90% времени работа передачи одно парой зубьев, а после её выхода из зацепления передача нарушается и происходит удар. Это конечно недопустимо, поэтому при проектировании передачи следует обеспечить величину коэффициента не менее 1. Расчет этого коэффициента для случая внешнего зацепления производится с помощью следующей зависимости:
εα 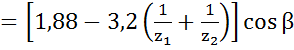
Для внутреннего зацепления знак + в скобке следует заменить на минус.
Нарезание зубьев производится либо с помощью фрезерования на цилиндрической заготовке пазов между зубьями пальцевыми или дисковыми фрезами или с помощью червячных фрез и рейки - фрезы. Второй способ называется методом огибания и дает более высокую точность особенно по шагу зуба.
Точность зубчатых колес нормируется по трем параметрам:
1. Норма кинематической точности.
2. Норма плавности.
3. Норма контакта.
| Эталон |
| Испытуемое колесо |
| Δα |
Норма плавности – колебание погрешности угла поворота в пределах одного оборота.
Норма контакта может быть определена путем покрытия краской рабочей поверхности зубьев одного колеса и оценкой площади закрашенной поверхности на зубьях другого колеса после вращения зубчатых колес.
Пятно показывает, что контакт зубьев происходил не по всей рабочей поверхности, а лишь по её части.
Существует 12 степеней точности; наиболее используемые в химическом и нефте-газовом машиностроении с 6 по 10. Причем нормирование происходит отдельно по трем параметрам например:
8-7-8 В
Это означает: 8- норма кинематической точности; 7 – норма плавности; 8- норма контакта. Кроме этого задается сопряжение зубьев – величина зазора между неработающими поверхностями зубьев.
Стандарт устанавливает шесть видов сопряжения: H – нулевой зазор, E – малый зазор, D и C – уменьшенный зазор, B – нормальный зазор, A – увеличенный зазор. В химическом и нефтегазовом производствах используются в основном передачи с нормальным, увеличенным и уменьшенным зазорами. Сопряжение дополняется допуском на боковой зазор, обозначаемым малой буквой. Всего установлено восемь видов допусков: a, b, c, d, h, x, y, z. Полное обозначение точности цилиндрической зубчатой передачи записывается следующим образом: 7-8-7-Ва ГОСТ 1643-81. Норма кинематической точности 7, норма плавности 8, норма контакта 7, сопряжение В, допуск бокового зазора – а.
При работе зубчатой передачи в зацеплении на линии контакта зубьев «на схеме это её проекция - полюс зацепления П» действуют силы. Они направлены по нормали к рабочей поверхности зубьев. Нормалью является линия зацепления.
| П |
| Fn1 |
| Fn2 |
Для удобства анализа нормальная сила раскладывается на проекции: Ft Fr Fa - соответственно тангенциальную (окружную), направленную по касательной к начальной окружности; радиальную, направленную к центру зубчатого колеса; осевую, направленную параллельно оси зубчатого колеса. Если передача прямозубая, то осевой силы Fa в передаче не возникает; все силы действуют в плоскости перпендикулярной оси колеса. Таким образом в прямозубой передаче нормальная сила в зацеплении раскладывается на две составляющие - Ft и Fr . Их связь с нормальной силой Fn определяется из следующей схемы:
| Fn |
| Fr |
| Ft |
| αω |
| П |
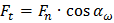 .
.
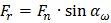
Однако, удобнее определять эти составляющие усилия в передаче через известные параметры передачи, а именно передаваемый крутящий момент Т и диаметр начальной окружности 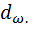
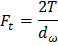
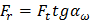
В приведенных формулах все величины, кроме 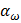 должны иметь индексы, указывающие на принадлежность шестерне или колесу. Например:
должны иметь индексы, указывающие на принадлежность шестерне или колесу. Например:

Здесь индекс 1 означает принадлежность всех величин шестерне.
Упрощенно цилиндрическая зубчатая передача и схема сил действующих в ней может быть представлена в следующем виде:
| Ft2 |
| Ft1 |
| Fr2 |
| Fr1 |
На схеме шестерня (меньшее по диаметру зубчатое колесо) и колесо (большее по диаметру) условно не контактируют для того чтобы была ясность к чему приложены силы. Силы, действующие на шестерню имеют индексы -1; а силы действующие на колесо - индексы -2.
Контрольные вопросы к лекции 3
1. Изобразите упрощенную схему цилиндрической зубчатой передачи и укажите величину межосевого расстояния.
2. На схеме укажите, какое зубчатое колесо является шестерней, а какое колесом.
3. Дайте определение модуля передачи.
4. Назовите кривую образующую рабочую поверхность зуба.
5. Что определяет коэффициент торцевого перекрытия?
6. Изобразите схему сил действующих в цилиндрической прямозубой передаче.
7. Какие нормы определяют степень точности передачи, определите их смысл.
8. Запишите связь окружной силы в передаче с величиной крутящего момента и размерами зубчатого колеса.
Лекция №4
Тема лекции: Критерии работоспособности зубчатых передач.
Потеря работоспособности зубчатых передач происходит из-за одной или совокупности следующих причин.
| Рис. 4.1 Разрушение зубьев |
1. Усталостное выкрашивание: выпадение с рабочей поверхности зуба частиц металла. В результате уменьшается площадь рабочей поверхности зуба и возникают концентраторы напряжений около образовавшихся ямок, что приводит к ускорению процесса выкрашивания.
2. Излом зуба у основания от напряжений изгиба.
3. Пластические деформации поверхности зуба.
4. Поверхностный износ.
| Рис. 4.2 Виды передач |
Открытые передачи не имеют корпуса и надежной смазки и поэтому не защищены от воздействия пыли, грязи и влаги. Поэтому, для них причинами потери работоспособности являются износ от трения поверхностей зубьев, пластические деформации и поломка зуба от ударов и перегрузок.
Закрытые передачи имеют закрытый корпус и масляную ванну, в которую погружаются зубья колес и при их вращении смазка попадает в зону зацепления, исключая контакт поверхностей зубьев по металлу, заменяя его контактом через масляную пленку. Это резко уменьшает износ зуба, повышая срок службы и, поэтому потеря работоспособности происходит из-за усталостного выкрашивания поверхности, пластических деформаций и поломки зуба при перегрузках.
Большая часть зубчатых передач выполняется в закрытом варианте, и потеря работоспособности происходит по механизму усталостного выкрашивания. Причиной этого является следующий процесс. Рабочая поверхность зуба подвергается нагружению и деформации при контакте с зубом сопряженного зубчатого колеса. Этот процесс имеет циклический характер.
| t |
| σ |
| Цикл нагружения |
| Рис. 4.3 Циклограмма нагружения |
| Fn |
| A |
| σH |
| A |
| Рис. 4.4 Нагружение зуба |
Силы Fn, действующие в зоне контакта зубьев вызывают местную деформацию с образованием площадки контакта-А. На этой площадке возникают контактные напряжения -σH, максимальная величина которых является мерой напряженного состояния зуба и служит причиной накопления усталостных явлений и выкрашивания поверхностных слоев. Контактные напряжения возникают в деталях, у которых при работе площадь поверхности соприкосновения с другой деталью несоизмеримо мала по сравнению с размерами самой поверхности детали. Максимальная величина возникающих при этом напряжений может быть рассчитана с помощью теории контактных напряжений Герца (Herz). Она позволяет связать величину этих напряжений с размерами и формой поверхности тел и приложенными усилиями. Формула Герца имеет вид.
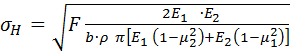 . (4.1)
. (4.1)
Здесь 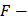 нормальная к поверхности контакта сила;
нормальная к поверхности контакта сила;
 - длина линии контакта (для зубчатых колес это ширина колеса);
- длина линии контакта (для зубчатых колес это ширина колеса);
 - приведенный радиус кривизны контактирующих поверхностей;
- приведенный радиус кривизны контактирующих поверхностей;
 . (4.2)
. (4.2)
 радиусы кривизны двух поверхностей;
радиусы кривизны двух поверхностей;
Знак + относится к случаю внешнего контакта -
Знак – относится к случаю внутреннего контакта -
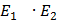 - модули упругости материалов контактирующих тел;
- модули упругости материалов контактирующих тел;
μ1 и μ2 – коэффициенты Пуассона материалов зубчатых колес.
Для обеспечения работоспособности зубчатых передач величина действующих контактных напряжения не должна превышать определенной их величины. Для определения этой величины проводятся испытания материалов при различных значениях рабочих контактных напряжений, и фиксируется время начала усталостного выкрашивания. В результате получаем зависимость следующего вида.
| σH |
| N |
| σHO |
| N МЦ |
| NHO |
I
σH1
| Рис. 4.5 Кривая выносливости |
NH1
Это зависимость контактной выносливости. Над кривой находится зона разрушения – здесь происходит потеря работоспособности. Под кривой- рабочая зона. На горизонтальной оси – N фиксируется число циклов нагружения до момента начала интенсивного усталостного выкрашивания. На графике видно, что при напряжении равном и меньшем величины σHO усталостное выкрашивание не происходит и срок службы детали при контактном нагружении стремится к бесконечности. Это напряжение является одной их механических характеристик материала и называется пределом контактной выносливости. И для этого случая нагружения выделяется зона III называемая зоной неограниченной выносливости. Ей соответствует число циклов нагружения NHO называемое базовым числом циклов нагружения. Если величина контактных напряжений велика, то потеря работоспособности передачи происходит из-за развития пластической деформации рабочей поверхности зубьев. Работа в таких условиях ограничивается малым числом циклов нагружения N МЦ т.е. малым сроком службы и называется малоцикловым разрушением. Работа в таком режиме нагружения на кривой контактной выносливости соответствует первой зоне.
Наиболее интересной является вторая зона – зона ограниченной выносливости. При работе в ней имеет место зависимость между действующей величиной контактных напряжений и предельным числом циклов нагружения (т.е. сроком службы) до момента начала заметного усталостного выкрашивания. При работе с контактными напряжениями σH1 можем прогнозировать срок службы (число циклов нагружения) - NH1. Наоборот, если известен требуемый ресурс - срок службы передачи, то можно рассчитать число циклов нагружения за этот срок и определить величину допустимых контактных напряжений и использовать её в проектном расчете передачи.
Однако, на практике определение расчетных контактных напряжений требует учета целого ряда дополнительных факторов. Во первых, для определения этого напряжения удобно использовать одну из характеристик материала зубчатого колеса, а именно предел контактной выносливости - σHO. Учет требуемого числа циклов нагружения Ni производится с помощью коэффициента долговечности KHL.
 , (4.3)
, (4.3)
Здесь: m – показатель кривизны кривой контактной выносливости на участке второй зоны, при расчете на выносливость он равен 6;
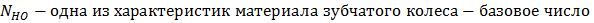
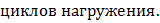
Эта величина определяется в зависимости от твердости поверхностного слоя материала.
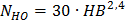 .
.
HB – средняя твердость материала по шкале твердости Бринелля. Средняя твердость используется потому, что термообработка - процесс не позволяющий получить точное значение твердости, а дающий некоторый вероятностный интервал, например 270…295 HB. Среднее значение этого интервала и используется в расчете.
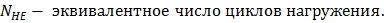 Эта величина учитывает фактическое число циклов нагружения и режим нагружения.
Эта величина учитывает фактическое число циклов нагружения и режим нагружения.
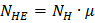 . (4.4)
. (4.4)
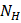 - фактическое число циклов нагружения.
- фактическое число циклов нагружения.

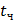 - ресурс работы зубчатого колеса в часах;
- ресурс работы зубчатого колеса в часах;
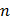 - частота вращения зубчатого колеса в оборотах в минуту;
- частота вращения зубчатого колеса в оборотах в минуту;
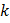 - коэффициент, учитывающий кратность зацепления (т.е. со сколькими зубчатыми колесами зацепляется данное зубчатое колесо).
- коэффициент, учитывающий кратность зацепления (т.е. со сколькими зубчатыми колесами зацепляется данное зубчатое колесо).
| Рис. 4.6 |
k=1 k=2
Левая схема: оба зубчатых колеса зацепляются с одним зубчатым колесом - кратность зацепления для каждого из этих колес равна 1. Правая схема: центральное зубчатое колесо зацепляется с двумя зубчатыми колесами, за один оборот каждый его зуб вступает в контакт с зубьями малых зубчатых колес (шестерен) два раза, кратность зацепления для него равна 2. У малых зубчатых колес (шестерен) каждый их зуб за один оборот шестерни вступает в контакт с зубьями большего по диаметру зубчатого колеса (колесом) один раз. Поэтому для каждой шестерни правой схемы кратность зацепления равна 1.
Выражение 4.4 содержит коэффициент  . Этот коэффициент учитывает режим нагружения, в котором работает рассчитываемое зубчатое колесо. Существует 6 типовых режимов нагружения.
. Этот коэффициент учитывает режим нагружения, в котором работает рассчитываемое зубчатое колесо. Существует 6 типовых режимов нагружения.
| Рис. 4.7 Типовые режимы нагружения |
| Fi/Fmax 1 |
| 1 ti/tΣ |
При работе конструкции нагрузка обычно изменяется во времени и при проектировании обычно оговаривается наиболее вероятный режим нагружения.
0 – постоянный режим;
1 - тяжелый режим;
2- средний равновероятностный;
3 – средний нормальный;
4 – легкий;
| Fi/Fmax 1 |
| ti/t Σ |
Учет влияния на выносливость фактического режима нагружения и производится с помощью коэффициента 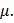
Этот коэффициент может принимать следующие значения.
Таблица 4.1
| № режима | ||||||

| 0,5 | 0,25 | 0,18 | 0,125 | 0,063 |
Определяемый выражением 4.3 коэффициент режима нагружения 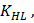 для материалов с однородной структурой может принимать значение в интервале от 1 (при равенстве расчетного и базового чисел циклов нагружения) до 2,6 на границе I зоны, где начинает работать другой механизм потери работоспособности. Для материалов с поверхностной термообработкой (ХТО, закалка ТВЧ) верхняя граница – 1,8.
для материалов с однородной структурой может принимать значение в интервале от 1 (при равенстве расчетного и базового чисел циклов нагружения) до 2,6 на границе I зоны, где начинает работать другой механизм потери работоспособности. Для материалов с поверхностной термообработкой (ХТО, закалка ТВЧ) верхняя граница – 1,8.
Здесь следует отметить, что зона III на кривой контактной выносливости, строго говоря, не гарантирует полного отсутствия развития усталостных процессов при работе в ней. Поэтому для полной гарантии выработки деталью требуемого ресурса, при расчете допускаемого контактного напряжения необходимо учитывать коэффициент долговечности, определяемый зависимостью 4.3, но значение коэффициента m для третьей зоны следует принимать равным 20.
Закладываемая в расчет величина σHO – предел контактной выносливости не является константой, а определяется с учетом твердости поверхностного слоя материала.
Таблица 4.2
| Термообработка | Твердость поверхности | Материал | σHO |
| Нормализация или улучшение | < 350 HB | Сталь углеродистая и легированная | 2 HBср +70 |
| Закалка поверхностная или обьемная | 40…56 HRC | 17 HRCср + 200 | |
| Цементация | Ø 56 HRC | Сталь легированная | 23 HRCср |
| азотирование | >52 HRC |
Таким образом, закладываемое в проектный расчет контактное напряжение будет определяться зависимостью:
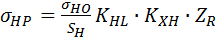 . (4.6)
. (4.6)
Здесь появляется коэффициент 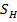 - коэффициент запаса, который принимается равным 1,1 для материалов с однородной объемной термообработкой и равным 1,2 с поверхностной термообработкой. Коэффициент
- коэффициент запаса, который принимается равным 1,1 для материалов с однородной объемной термообработкой и равным 1,2 с поверхностной термообработкой. Коэффициент 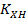 учитывает возможную реверсивность нагрузки, а коэффициент
учитывает возможную реверсивность нагрузки, а коэффициент 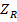 учитывает шероховатость поверхности зуба.
учитывает шероховатость поверхности зуба.
Контрольные вопросы к лекции 4
1. Перечислите виды разрушения зубчатых колес.
2. В чем различие между открытой и закрытой зубчатыми передачами?
3. Какую роль играет смазка при работе зубчатой передачи?
4. В каких случаях возникают контактные напряжения?
5. Какие механические характеристики материалов зубчатых колес определяют величину действующих контактных напряжений?
6. Что такое σHO?
7. Что определяет коэффициент 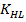 ?
?
8. Что учитывает коэффициент кратности зацепления?
9. Чем отличаются различные режимы нагружения?
10. Почему коэффициент долговечности не может быть большим 2,6?
Лекция №5
Тема лекции: Расчет цилиндрических зубчатых передач на контактную выносливость.
Смысл расчета заключается в определении действующих в передаче контактных напряжений и сравнении их с допускаемыми напряжениями. Расчет основан на формуле Герца (4.1).
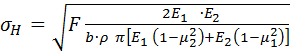 .
.
| r |
| t |
| a |
| Fn |
| αω |
| Ft |
| Fr |
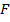 – нормальной, т. е. перпендикулярной к поверхности контакта зубьев силы.
– нормальной, т. е. перпендикулярной к поверхности контакта зубьев силы.
| Рис. 5.1 Силы в зубчатой передаче |
| a |
| t |
| Fn |
Анализ проведем для прямозубой передачи. Сила  для удобства анализа раскладывается на две проекции. В направлении оси t касательной к начальной окружности колеса и перпендикулярной к его оси – проекция Ft – окружная (или тангенциальная)сила. Она связана с нормальной силой через угол зацепления αω. Вторая проекция Fr – радиальная сила.
для удобства анализа раскладывается на две проекции. В направлении оси t касательной к начальной окружности колеса и перпендикулярной к его оси – проекция Ft – окружная (или тангенциальная)сила. Она связана с нормальной силой через угол зацепления αω. Вторая проекция Fr – радиальная сила.
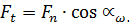 (5.1)
(5.1)
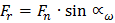 .
.
Для нахождения нормальной силы 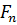 воспользуемся первым выражением из (5.1) и соотношением:
воспользуемся первым выражением из (5.1) и соотношением:

Тогда сможем найти выражение для 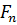 .
.

В этом выражении присутствует крутящий момент на колесе, который либо задается при проектировании передачи, либо определяется по заданным при проектировании величине передаваемой мощности Р и частоте вращения колеса n.
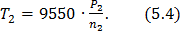
Угол зацепления 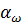 для эвольвентных передач равен 200. Неизвестным является только диаметр начальной окружности
для эвольвентных передач равен 200. Неизвестным является только диаметр начальной окружности  . Он будет выражен через межосевое расстояние передачи и её передаточное число. Вторая величина, которую следует выразить через параметры зубчатой передачи – b
. Он будет выражен через межосевое расстояние передачи и её передаточное число. Вторая величина, которую следует выразить через параметры зубчатой передачи – b  - длина контактирующих поверхностей
- длина контактирующих поверхностей  Для прямозубой передачи это ширина зубчатого венца (ширина колеса) - b
Для прямозубой передачи это ширина зубчатого венца (ширина колеса) - b 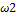 . Она может быть выражена через межосевое расстояние
. Она может быть выражена через межосевое расстояние
Дата добавления: 2014-12-30; просмотров: 289; Мы поможем в написании вашей работы!; Нарушение авторских прав |