
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В.В какой координатной четверти пересекаются прямые и ?A) В четвёртой 4 страница
Найти неопределённый интеграл  E)
E) 
Найти неопределённый интеграл  E)
E) 
Найти область определения функции  .E)
.E) 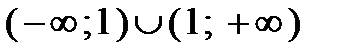
Найти область определения функции  Е)
Е) 
Найти определитель  .E) 10
.E) 10
Найти определитель  E)
E) 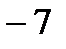
Найти определитель  E) 0
E) 0
Найти определитель 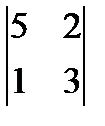 E) 13
E) 13
Найти площадь параллелограмма, построенного на векторах  ,
,  .E)
.E) 
Найти предел  .E)
.E) 
Найти предел  .E)
.E) 
Найти предел  .E) 2
.E) 2
Найти предел  .Е)
.Е) 
Найти предел функции, используя правило Лопиталя:  .E)
.E) 
Найти предел  .E)
.E) 
Найти предел  .E) 1,5
.E) 1,5
Найти производную 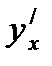 параметрически заданной функции
параметрически заданной функции  .E)
.E) 
Найти производную 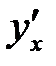 функции, заданной параметрически:
функции, заданной параметрически:  E)
E) 
Найти производную 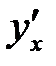 функции, заданной параметрически:
функции, заданной параметрически:  E)
E) 
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 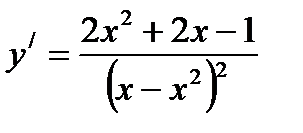
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 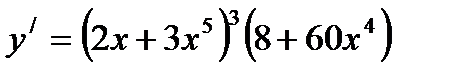
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 
Найти производную функции  .E)
.E) 
Найти расстояние между точками  и
и  .E) 13
.E) 13
Найти расстояние от точки 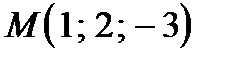 до плоскости
до плоскости  .E) 0
.E) 0
Найти скалярное произведение 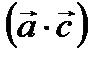 векторов
векторов 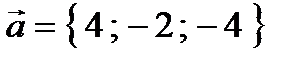 ,
,  .E) 2
.E) 2
Найти смешанное произведение векторов  .E) 0
.E) 0
Найти такие значения m и n, чтобы прямая  была перпендикулярна к плоскости
была перпендикулярна к плоскости  .E)
.E)  ,
, 
Найти уравнение касательной к графику функции 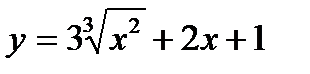 в точке, абсцисса которой
в точке, абсцисса которой  .E)
.E) 
Найти уравнение нормали к кривой  в точке с абсциссой
в точке с абсциссой  .E)
.E) 
Найти уравнение плоскости, проходящей через начало координат перпендикулярно к вектору  , где
, где  ,
,  .E)
.E) 
Найти уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  E)
E) 
Найти уравнение прямой, отсекающей на координатных осях Ох и Оу отрезки величиной соответственно 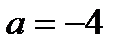 и
и  .E)
.E) 
Найти уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  .E)
.E) 
Найти, чему равно алгебраическое дополнение элемента  определителя
определителя 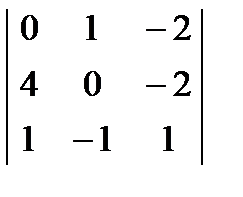 . E) –4
. E) –4
Найти, чему равно алгебраическое дополнение элемента  определителя
определителя  E)
E) 
Найти, чему равно алгебраическое дополнение элемента  определителя
определителя  E)
E) 
Написать канонические уравнения прямой, проходящей через точку  параллельно вектору
параллельно вектору  .C)
.C) 
Написать общее уравнение прямой, отсекающей на оси Ох отрезок величиной  , а на оси Оу - отрезок величиной
, а на оси Оу - отрезок величиной  .C)
.C) 
Написать уравнение плоскости, проходящей через точки  .C)
.C) 
Написать уравнение прямой, проходящей через точку  параллельно прямой
параллельно прямой  .C)
.C) 
Написать уравнение прямой, проходящей через точку 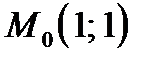 перпендикулярно вектору
перпендикулярно вектору  .C)
.C) 
О.Определите все критические точки функции  .E)
.E)  ,
, 
Определите длину вектора  .Е) 3
.Е) 3
Определите количество точек максимума функции 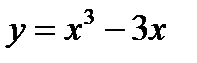 .E) 1
.E) 1
Определите множество, на котором функция  монотонно убывает.E)
монотонно убывает.E) 
Определите, чему параллельна плоскость  E) оси Oz
E) оси Oz
Определите, чему равен предел  .E)
.E) 
Определитель  =?B)
=?B) 
Определитель  =?B) 0
=?B) 0
Определить величину предела  .E) –0,5
.E) –0,5
Определить расстояние от точки  до плоскости
до плоскости  .E) 1
.E) 1
Определить, при каких значениях k и b прямая  параллельна прямой
параллельна прямой  .E)
.E) 
Определить, при каком значении m прямая  проходит через начало координат.E) при
проходит через начало координат.E) при  и при
и при 
Определить, чему равен предел  .E) 2
.E) 2
П.Перемножить матрицы:  .A)
.A) 
Плоскость  D) …параллельна оси Oz
D) …параллельна оси Oz
Предел  равен A)
равен A) 
Предел  равен A)
равен A) 
Предел  равен A) 0
равен A) 0
Предел  равен A) 0,5
равен A) 0,5
Предел  равен A) 2
равен A) 2
Предел  равен?A)
равен?A) 
Предел 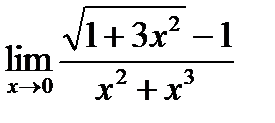 равен?A)
равен?A) 
Предел  равен?A)
равен?A) 
Предел  равен?A)
равен?A) 
Предел  =?A)
=?A) 
Предел  =?A) 2
=?A) 2
Предел  равен A) 2
равен A) 2
Предел  равен A) –3
равен A) –3
Предел  равен?A)
равен?A) 
Предел  = ?A) 2
= ?A) 2
При заданных координатах концов  и
и  найти вектор
найти вектор  .С)
.С) 
При каких значениях k и b прямая  параллельна прямой
параллельна прямой  ?C)
?C) 
При каких значениях m и n прямая  перпендикулярна плоскости
перпендикулярна плоскости  ?C)
?C)  ,
, 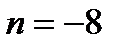
При каком k прямая  перпендикулярна прямой
перпендикулярна прямой  ?C)
?C) 
При каком значении чисел m и n прямые 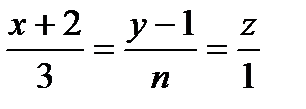 и
и  параллельны?C)
параллельны?C)  ,
, 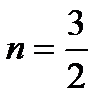
При пересечении с осями координат Ох и Оу прямая отсекает от них отрезки величиной  и
и  соответственно. Составить уравнение прямой.C)
соответственно. Составить уравнение прямой.C) 
Применив правило Лопиталя, найдите предел функции:  .C) 0
.C) 0
Продифференцировать функцию  .D)
.D) 
Продифференцируйте функцию  .C)
.C) 
Продифференцируйте функцию  .C)
.C) 
Продифференцируйте функцию  .C)
.C) 
Проекция вектора  на направление вектора
на направление вектора  равнаC)
равнаC) 
Проекция вектора  на направление вектора
на направление вектора 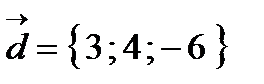 равна C)
равна C) 
Производная 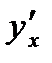 от параметрически заданной функции
от параметрически заданной функции  равнаA)
равнаA) 
Производная функции  равнаA)
равнаA) 
Производная функции  равна A)
равна A) 
Производная функции  равна A)
равна A) 
Производная функции  равна:A)
равна:A) 
Производная функции  равнаA)
равнаA) 
Проинтегрировать:  A)
A) 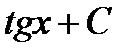
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Проинтегрировать:  A)
A) 
Прямая отсекает на координатных осях Ох и Оу отрезки величиной  и
и  соответственно. Составить уравнение прямой.A)
соответственно. Составить уравнение прямой.A) 
Прямая проходит через начало координат и точку  . Составить уравнение прямой.A)
. Составить уравнение прямой.A) 
Прямая проходит через точку  перпендикулярно плоскости
перпендикулярно плоскости  . Составить уравнение прямой.A)
. Составить уравнение прямой.A) 
Р.Размерность матрицы 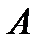 равна
равна  , размерность
, размерность  -
- 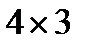 , размерность
, размерность 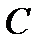 -
-  . Какую из указанных ниже операций нельзя выполнить?A)
. Какую из указанных ниже операций нельзя выполнить?A) 
Размерность матрицы  равна 2´3, матрицы
равна 2´3, матрицы  - 3´5. Какую размерность имеет матрица
- 3´5. Какую размерность имеет матрица 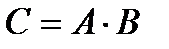 ?A) 2´5
?A) 2´5
Размерность матрицы  равна 3´5, матрицы
равна 3´5, матрицы  - 5´4. Какую размерность имеет матрица
- 5´4. Какую размерность имеет матрица 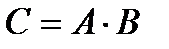 ?A) 3´4
?A) 3´4
Расстояние между точками  и
и  равно E)
равно E) 
Расстояние от точки  до плоскости
до плоскости  равно E)
равно E) 
Дата добавления: 2014-12-30; просмотров: 284; Мы поможем в написании вашей работы!; Нарушение авторских прав |