Кай жағдайда денені материалдық нүкте деп қарастыруға болады?

Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рас­смотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуляции вектора Н (см. (133.10)), введя в ее правую часть полный ток I_полн = j_полнdS сквозь поверхность S, натянутую на замкнутый контур L. Тогдаобобщенная теорема о циркуляции вектора Н запишется в виде

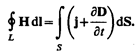(138.4)

Выражение (138.4) справедливо всегда, свидетельством чего является полное соответст­вие теории и опыта.

§ 139. Уравнения Максвелла для электромагнитного поля

Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зре­ния не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле (см. § 137) может быть как потенциальным (Е_Q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е=Е_Q +Е_B. Так как цир­куляция вектора Е_Q равна нулю (см. (137.3)), а циркуляция вектора Е_B определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

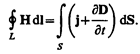
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущими­ся зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

(139.1)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью r, то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где e₀ и m₀ — соответственно электрическая и магнитная постоянные, e и m — соответст­венно диэлектрическая и магнитная проницаемости, g — удельная проводимость веще­ства.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Мак­свелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму допол­няют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла — наиболее общие уравнения для электрических и магнит­ных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что перемен­ное магнитное поле всегда связано с порождаемым им электрическим полем, а пере­менное электрическое поле всегда связано с порождаемым им магнитным, т. е. элект­рическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Теория Максвелла, являясь обобщением основных законов электрических и магнит­ных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3×10⁸ м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экс­периментально подтверждена.

К электромагнитному полю применим только принцип относительности Эйн­штейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относи­тельности Галилея.

Согласно принципу относительности Эйнштейна, механические, оптические и элект­ромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.

Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Taк, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета про­водник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.

Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, маг­нитных и оптических явлений, базирующейся на представлении об электромагнитном поле.

Кай жағдайда денені материалдық нүкте деп қарастыруға болады?

<variant> Қарастырылып отырған жағдайда өлшемі мен пішінін ескермеуге болатын денені

<variant> Массасы өте аз денені

<variant> Барлық жағдайда екі нүктесінің ара қашықты ғы тұрақты дене

<variant> Жылдамдығы өте кіші денені

<variant> Кез-келген қатты дене