
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поняття інформації та сигналу в ТС
Тенденції розвитку радіотехніки зумовили широке впровадження автоматичних і автоматизованих систем управління, для дослідження і проектування яких необхідне використання системно-інформаційного аналізу. У цьому випадку дослідження ТС пов'язано з поняттями інформаційного опису: ентропія, інформація, кількість інформації, кодування та іншими, що належать до статистичної теорії інформації.
Під час зростання обсягів знань, накопичуваних людством, збільшувалася кількість переданої інформації. Це вимагало вирішення ряду технічних проблем, пов'язаних зі швидкістю передачі, переробленням інформації, її кодуванням і розшифровкою, перетворенням сигналів на вході й виході каналу зв'язку між джерелом інформації та її споживачем. У середині ХХ в. під час бурхливого розвитку науки й техніки зросла роль інформації як засобу спілкування між людьми, між людиною і машиною, між машинами. Лавиноподібне зростання інформації в другій половині ХХ в., що одержало назву інформаційного вибуху, зажадало наукового підходу до інформації, до виявлення її характерних властивостей.
Теорією інформації називають науку, що вивчає кількісні закономірності, пов'язані з одержанням, передачею, обробленням і зберіганням інформації. Теорія інформації, яка виникла в 40-х роках ХХ століття із практичних завдань теорії зв'язку, в цей час стає необхідним математичним апаратом під час вивчення різних процесів керування та систем, в яких можна виділити джерело, приймач і канал передачі інформації.
| Приклад | У 1948 р. К. Шеннон опублікував роботу “Математична теорія зв’язку”. Ще в 1921 р. Р.Е. Фішер уперше зробив спробу зв'язати кількість інформації з імовірністю і обґрунтував статистичне визначення інформації; в 1924 р. Г. Найквіст запропонував логарифмічне оцінювання впливу швидкості передачі на кількість переданих повідомлень; у 1928 р. було надруковано роботу Р. Хартлі, в якій розглядалися “практичні міри інформації” з використанням логарифмічного оцінювання; Л. Сцилард у 1929 р. уперше вказав на наявність співвідношення між інформацією і ентропією; в 1933 р. В.А. Котельников надрукував роботу, яка містила “теорему відліків”, а в 1934 р. К.Р. Поппер запропонував ідею оцінювання інформації на основі аналізу альтернатив, що виключаються під час одержання повідомлення. Однак у світовій науковій літературі вважається, що саме 1948 р. – рік зародження теорії інформації й кількісного підходу до інформаційних процесів. |
Неважко помітити, що всі обчислювальні машини (ЕОМ, контролери, логічні пристрої, що програмуються, та ін.) належать до інформаційних систем, основна відміна яких від енергетичних систем полягає в тому, що у них головним об’єктом передачі є інформація, а не енергія. ЕОМ як інформаційна система являє собою сукупність технічних засобів, призначених для формування, передачі, перетворення, перероблення, зберігання й використання інформації. Отже, взаємодія арифметичного (АП) та запам’ятовувального (ЗП) пристроїв в ЕОМ – це класична схема теорії зв’язку (рис.1, а). У загальному випадку, враховуючи процеси оброблення інформації в ЕОМ, цю схему можна подати у іншому вигляді (рис. 1.б), на якому введені наступні позначення: КП – керувальний пристрій; ВхП і ВихП – вхідний (кодувальний) і вихідний (декодувальний) пристрої відповідно.

Рис. 1. Схема перероблення інформації в обчислювальних пристроях: а – взаємодія АП та ЗП; б – загальна схема перероблення інформації
Сучасне розуміння інформації склалося не відразу; вона являла собою сукупність знань, отриманих різними науками: фізикою, біологією, теорією інформації та ін. Хоча фізика намагалася вивчати природні явища в максимально незв'язаній з людиною і її впливом формі, їй не вдалося повністю виключити людський фактор. Це зумовлено такими причинами:
1. При експериментальному дослідженні фізичних явищ не можна обійтися без вимірювання багатьох величин, а без впливу людини не проводяться навіть автоматичні експерименти.
2. Дослідження фізикою технічних пристроїв привело до того, що в їхньому поводженні виявилися сліди людської діяльності (уперше це було помічено в термодинаміці – науці, що вивчає процеси в теплових машинах).
3. Часто припускається, що спостереження ведеться безпосередньо за самою системою Х. Однак на практиці може виявитися, що вона недоступна для спостереження і з'ясовується стан не цієї системи, а деякої іншої системи Y, зв'язаної з нею.
| Приклад | Замість безпосереднього спостереження за повітряними цілями ведеться спостереження за екраном відображення повітряної обстановки, на якому цілі зображено умовними позначками; замість безпосереднього спостереження за космічним кораблем ведеться спостереження за системою сигналів, переданих його апаратурою; замість тексту Х відправленої телеграми одержувач спостерігає текст Y прийнятої телеграми, який не завжди збігається з Х, і т.д. |
При цьому розходження між системою Х і системою Y, що піддається безпосередньому спостереженню, можуть бути двох типів:
- розходження через те, що деякі стани системи Х не відображаються системою Y;
- розходження через помилки (неточності вимірювання параметрів системи Х і неточності під час передачі повідомлень).
| Приклад | Розходженнями першого типу є розходження, що виникають під час округлення числових даних або наближеного опису властивостей системи Х системою Y, що відображає її. Розходженням другого типу є перекручування сигналів, що виникають унаслідок перешкод у каналах зв'язку, несправностей апаратури та неуважності людей, що беруть участь у передачі інформації, та ін. |
Виявилося, що без введення спеціального поняття ентропії (від гр. entropy – перетворення) неможливо описати дії технічних пристроїв. Стрибок у розумінні природи ентропії відбувся, коли Л. Больцман дав її статичну інтерпретацію (1877 р.). Він кинув фразу, що “… ентропія характеризує відсутню інформацію”, але тоді його ніхто не зрозумів.
Після побудови К. Шенноном теорії інформації виявилося, що формула Шеннона для інформаційної ентропії та формула Больцмана для термодинамічної ентропії збігаються.
Для системного аналізу поняття інформації так само фундаментальне, як поняття енергії для фізики. Адже справедливим вважається таке означення кібернетики, запропоноване А.Н. Колмогоровим: кібернетика – це наука, що займається вивченням систем будь-якої природи, здатних сприймати, зберігати і переробляти інформацію та використовувати її для керування і регулювання.
Інформація – це властивість матерії, яка полягає у тому, що внаслідок взаємодії об'єктів установлюється певна відповідність. Чим сильніше виражено цю відповідність, тим повніше стан одного об'єкта відбиває стан іншого, тим більше інформації один об'єкт містить про інший.
| Примітка | Незважаючи на більш ніж піввікову дискусію, проблема “місця” поняття інформації в системі фундаментальних понять наукових знань залишається актуальною. До теперішнього часу сформувався цілий набір загальнонаукових поглядів, що пропонують розуміння суті феномена інформації. Більш того, починаючи з першої половини 90‑х років ХХ століття і до теперішнього часу спостерігається істотне відродження інтересу до проблеми феномена інформації. Формується визнане більшістю дослідників уявлення про те, що універсального означення інформації не існує. |
Слід розрізняти поняття ”інформація” і “повідомлення”. Повідомлення – це форма подання інформації. Під час передачі повідомлення має бути попередньо перетворено в сигнал. Сигнал – це матеріальний носій повідомлення, фізична величина, що змінюється та відображає повідомлення, засіб перенесення інформації в просторі та часі.
| Приклад | У сучасній техніці використовують електричні, електромагнітні, світлові, механічні, звукові, ультразвукові сигнали. Для передачі повідомлень необхідно застосовувати той насій, який ефективно поширюється по лінії зв'язку, що використовується. Наприклад, по провідній лінії зв'язку найбільш легко проходять постійний струм і змінні струми невисоких частот (не більше декількох кілогерц). По радіолінії ефективно поширюються електромагнітні коливання високих частот (від сотень кілогерц до десятків тисяч мегагерц). |
Як сигнали використовуються не об'єкти самі по собі, а їхні стани, причому не всякий стан має сигнальні властивості. Відповідність між сигналом та інформацією, що ним переноситься, встановлену за спеціальними правилами, називають кодом. У штучних системах кодом називають комплекс правил утворення сигналу (синонімом коду в техніці є модуляція), який покладено в основу роботи відповідних кодувальних пристроїв.
Математичний опис сигналів містить набір функцій параметра t (кожну таку функцію називають реалізацією) та ймовірнісну міру на множині реалізацій. Цей опис називають ансамблем. Він має такий вигляд:
 , (1)
, (1)
де 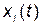 – реалізація сигналу в момент часу t;
– реалізація сигналу в момент часу t; 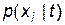 – імовірність появи реалізації
– імовірність появи реалізації 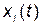 , причому
, причому  , m – кількість значних реалізацій сигналу.
, m – кількість значних реалізацій сигналу.
Пристрій, що здійснює вибір повідомлень з ансамблю повідомлень у системах перероблення інформації, називають джерелом повідомлень.
У зв'язку із цим ентропія 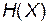 – міра невизначеності випадкової величини зі скінченним числом можливих значень, що зв’язана з одним символом (елементом, реалізацією) повідомлення (сигналу), тобто
– міра невизначеності випадкової величини зі скінченним числом можливих значень, що зв’язана з одним символом (елементом, реалізацією) повідомлення (сигналу), тобто
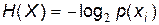 , (2)
, (2)
де 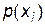 – імовірність (міра невизначеності) появи i-го елемента повідомлення.
– імовірність (міра невизначеності) появи i-го елемента повідомлення.
У загальному випадку ентропію можна виразити як кількість інформації, що припадає на одну реалізацію (відлік) сигналу, тобто як міру зняття невизначеності під час прийому сигналу. Використовуючи вираз (2), отримаємо
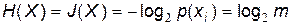 (3)
(3)
за умови, що 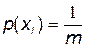 .
.
Особливе місце в статистичній теорії інформації займає питання вибору кількісної міри інформації. У виразах (2) – (3) ця міра двійкова, суть якої можна визначити як кількість інформації, що дорівнює двійковому логарифму від двох рівно ймовірних можливостей:
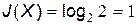 (біт),
(біт),
тобто одна двійкова одиниця (біт) являє собою результат вибору із двох рівно ймовірних можливостей.
| Примітка | Значення основи а логарифма під час вимірювання інформації та ентропії можуть бути різними, тому що вони визначають масштаб вимірювання. На сучасному етапі розвитку інформаційних систем крім бітів користуються такими одиницями виміру: при  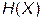 – у нітах; при – у нітах; при 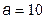 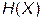 – у дітах. – у дітах.
|
У цьому випадку кількості інформації під час дослідження систем можна дати таке наочне тлумачення: вимірювання в бітах умовно характеризується кількістю відповідей “так” і “ні”, за допомогою яких можна одержати потрібну інформацію.
Приклад 1. Задумано деяке ціле число Х від 1 до 8 (  ). Необхідно його вгадати, поставивши мінімальну кількість запитань, на кожне з яких дається відповідь “так” або “ні”.
). Необхідно його вгадати, поставивши мінімальну кількість запитань, на кожне з яких дається відповідь “так” або “ні”.
Визначаємо інформацію, яка міститься в повідомленні: “Яке число задумано?” Апріорі всі значення Х від 1 до 8 однаково ймовірні, тобто  , отже, за виразом (3)
, отже, за виразом (3)
 .
.
Мінімальна кількість запитань, яку потрібно поставити для з'ясування задуманого числа, становить не менше від трьох, тобто якщо сформулювати запитання так, щоб імовірності відповідей “так” і “ні” були рівними, то достатньо трьох запитань.
Нехай, наприклад, задумано число 3, ми цього не знаємо й задаємо запитання:
Запитання 1. Число Х парне?
Відповідь: ні.
(Висновок: Х – одне з чисел 1, 3, 5, 7).
Запитання 2. Число Х менше за 5?
Відповідь: так.
(Висновок: Х – одне з чисел 1, 3).
Запитання 3. Це число 1?
Відповідь: ні.
(Висновок: число Х дорівнює трьом).
 2. Перетворення безперервних сигналів в дискретні
2. Перетворення безперервних сигналів в дискретні
Сигнал являє собою відображення повідомлення і може бути дискретним або безперервним. Визначимо, що всі реальні сигнали скінчені в часі. Тому будь-який сигнал подають у дискретному вигляді.
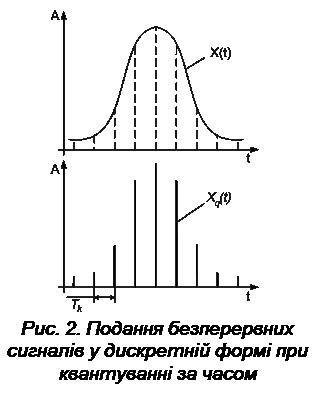
Квантування безперервних сигналів може бути проведено за часом (рис.2), за рівнем (рис. 3) або одночасно за рівнем і часом.
Квантування за часом полягає в заміні безперервного сигналу 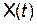 дискретним за часом сигналом
дискретним за часом сигналом 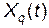 , значення якого для фіксованих моментів часу
, значення якого для фіксованих моментів часу  збігаються відповідно з миттєвими значеннями безперервного сигналу, унаслідок чого функція
збігаються відповідно з миттєвими значеннями безперервного сигналу, унаслідок чого функція 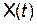 заміняється сукупністю миттєвих значень
заміняється сукупністю миттєвих значень  ,
, 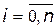 .
.
За миттєвими значеннями  можна відновити вихідну функцію з певною точністю на основі теорії відображення Найквиста – Котельникова, зокрема, на основі теореми відліків, яка базується на дискретній модуляції безперервних сигналів: будь-яка функція зі спектром, що знаходиться в інтервалі
можна відновити вихідну функцію з певною точністю на основі теорії відображення Найквиста – Котельникова, зокрема, на основі теореми відліків, яка базується на дискретній модуляції безперервних сигналів: будь-яка функція зі спектром, що знаходиться в інтервалі  , повністю визначається послідовністю її значень у точках, що знаходяться на відстані одна від одної на 1/2f одиниць часу.
, повністю визначається послідовністю її значень у точках, що знаходяться на відстані одна від одної на 1/2f одиниць часу.
Часовий інтервал 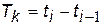 між двома сусідніми фіксованими моментами часу, у якому задається дискретна функція, називають інтервалом часового квантування, а величину
між двома сусідніми фіксованими моментами часу, у якому задається дискретна функція, називають інтервалом часового квантування, а величину 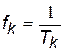 – частотою квантування.
– частотою квантування.

а б
Рис. 3. Квантування безперервних сигналів за рівнем: а – заміна функції 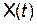 меншим дискретним значенням; б – заміна функції
меншим дискретним значенням; б – заміна функції 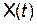 меншим або більшим дискретним значенням
меншим або більшим дискретним значенням
Квантування за рівнем здійснюється двома способами, коли миттєве значення функції 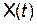 заміняється меншим дискретним значенням (рис. 5.3, а) або меншим чи більшим дискретним значенням (рис. 5.3, б) залежно від того, яке із цих значень ближче до миттєвого значення функції. При цьому під час передачі, зберігання або оброблення значення сигналу подається номером-кодом відповідного дискретного рівня.
заміняється меншим дискретним значенням (рис. 5.3, а) або меншим чи більшим дискретним значенням (рис. 5.3, б) залежно від того, яке із цих значень ближче до миттєвого значення функції. При цьому під час передачі, зберігання або оброблення значення сигналу подається номером-кодом відповідного дискретного рівня.
Приклад 2. Нехай задано безперервний аналоговий сигнал 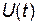 , обмежений смугою частот від 0 до 340 Гц (рис. 4). Зробити перетворення сигналу виду “аналог – код” для передачі його по каналу зв’язку при кількості рівнів квантування
, обмежений смугою частот від 0 до 340 Гц (рис. 4). Зробити перетворення сигналу виду “аналог – код” для передачі його по каналу зв’язку при кількості рівнів квантування 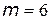 .
.
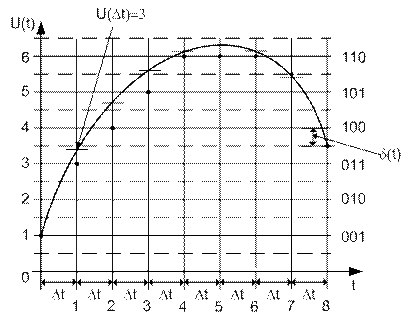
Рис. 4. Вид безперервного аналогового сигналу для прикладу 2
На початку зробимо операцію дискретизації, тобто перетворення функції безперервного часу у функцію, що квантується за часом. Координатами є миттєві значення функції, вилучені у зазначені моменти часу:
 мс.
мс.
Далі проведемо операцію квантування за рівнем. Вона зводиться до заміни будь-якого миттєвого значення функції 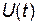 одним з дозволених значень рівня квантування, наприклад відповідно до рис. 3, б.
одним з дозволених значень рівня квантування, наприклад відповідно до рис. 3, б.
На рис. 4 миттєве значення 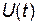 за рівнем позначимо горизонтальною рискою, а за часом – точкою (тобто
за рівнем позначимо горизонтальною рискою, а за часом – точкою (тобто 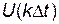 при
при 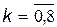 ). Якщо в цій точці значення функції
). Якщо в цій точці значення функції 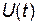 лежить в інтервалі
лежить в інтервалі 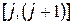 , то чисельно воно визначається шляхом присвоювання найближчого за величиною одного з двох кінцевих значень інтервалу
, то чисельно воно визначається шляхом присвоювання найближчого за величиною одного з двох кінцевих значень інтервалу 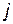 або
або  , тобто
, тобто  або
або 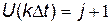 при
при 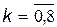 та
та  . У випадку, коли
. У випадку, коли  , то величина
, то величина 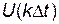 береться такою, що дорівнює
береться такою, що дорівнює 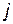 або
або  .
.
Наприклад, для першої риски (  ) числове значення безперервної функції
) числове значення безперервної функції 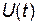 лежить в інтервалі, оскільки квантування значення
лежить в інтервалі, оскільки квантування значення 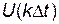 визначено до найближчого цілого числа, тобто
визначено до найближчого цілого числа, тобто 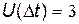 . Таким чином для всіх шости “рисок” функції
. Таким чином для всіх шости “рисок” функції 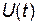 одержимо цифровий двійковий код
одержимо цифровий двійковий код 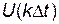 при
при 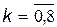 :
:
 – 1 (001);
– 1 (001);  – 3 (011);
– 3 (011);
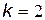 – 5 (101);
– 5 (101);  – 6 (110);
– 6 (110);
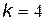 – 6 (110);
– 6 (110);  – 6 (110);
– 6 (110);
 – 6 (110);
– 6 (110);  – 5 (110);
– 5 (110);
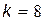 – 4 (100).
– 4 (100).
Отриману цифрову форму 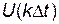 аналогового сигналу
аналогового сигналу 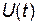 , поданого у вигляді кодової комбінації, зображено на рис. 5.5.
, поданого у вигляді кодової комбінації, зображено на рис. 5.5.
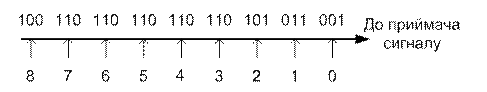
Рис. 5. Цифрова форма сигналу 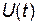
Максимальна кількість значущих станів за рівнем (кількість відліків) визначається співвідношенням
 , (4)
, (4)
де 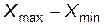 – діапазон зміни сигналу; Δk – крок квантування (різниця між сусідніми рівнями квантування); g – зведена середня квадратична похибка (у відсотках) або похибка, що відповідає кроку квантування.
– діапазон зміни сигналу; Δk – крок квантування (різниця між сусідніми рівнями квантування); g – зведена середня квадратична похибка (у відсотках) або похибка, що відповідає кроку квантування.
Під час квантування за рівнем з'являються методичні похибки, що пов'язані із заміною дійсного значення реальної функції її дискретним значенням. Цю похибку 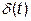 називають похибкою квантування за рівнем (шумом квантування). Використовуючи умови, наведені у прикладі 2, знайдемо шум квантування (див. рис. 4):
називають похибкою квантування за рівнем (шумом квантування). Використовуючи умови, наведені у прикладі 2, знайдемо шум квантування (див. рис. 4):
 . (5)
. (5)
| Примітка | Відомо, що реальна чутливість приймачів, органів чуття людини та інформаційно-вимірювальних систем обмежена роздільною здатністю. Тому не потрібно відтворювати безперервні сигнали з достатньо високою точністю. Крім того, наявність перешкод у каналах зв’язку та різних спотворень не дає можливості точно відтворювати передані сигнали. В цьому випадку в теорії інформації впроваджено поняття “епсілон-ентропія”, яка дорівнює середній кількості інформації в одному незалежному відліку безперервного випадкового сигналу, що є необхідною для відтворення цього сигналу із заданою середньоквадратичною похибкою. У подальшому мається на увазі саме ця ентропія. |
Похибка квантування  має випадковий характер, причому під час квантування за рівнем першим способом (див. рис. 3, а) ця похибка завжди від’ємна й змінюється в діапазоні
має випадковий характер, причому під час квантування за рівнем першим способом (див. рис. 3, а) ця похибка завжди від’ємна й змінюється в діапазоні 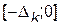 ; за другим способом – у діапазоні
; за другим способом – у діапазоні  . Закон розподілу
. Закон розподілу  залежить від закону розподілу функції
залежить від закону розподілу функції 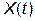 , але при досить великій кількості рівнів квантування закон розподілу
, але при досить великій кількості рівнів квантування закон розподілу  підпорядковується закону розподілу рівної ймовірності, а саме у таких випадках:
підпорядковується закону розподілу рівної ймовірності, а саме у таких випадках:
- при заміні дійсного значення функції найближчим меншим значенням
 (6)
(6)
з математичним сподіванням похибки квантування 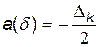 і дисперсією
і дисперсією  ;
;
- при заміні дійсного значення функції меншим або більшим дискретним значенням
 (7)
(7)
з математичним сподіванням похибки квантування 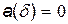 і дисперсією
і дисперсією  .
.
З урахуванням похибки d зведена середня квадратична похибка, що відповідає кроку квантування Δk, визначається таким виразом:
 за умови, що
за умови, що 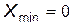 , (8)
, (8)
де N – кількість інтервалів, на які розбивається динамічний діапазон сигналу під час квантування, 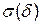 – середнє квадратичне значення похибки квантування.
– середнє квадратичне значення похибки квантування.
Реальна кількість значущих станів за рівнем (кількість відліків) на одиницю перевищує кількість інтервалів квантування, тобто
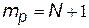 . (9)
. (9)
Приклад 3. Сигнал, переданий по каналу зв'язку, квантується за рівнем способом заміни його миттєвих значень найближчим меншим рівнем квантування. Визначити реальну кількість рівнів квантування сигналу за умови, що зведена середня квадратична похибка не перевищує 0,3 %.
При заданому способі квантування похибка квантування від’ємна із середнім квадратичним значенням відповідно до виразу (6)
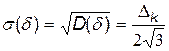 .
.
З урахуванням виразу (8) зведена середня квадратична похибка становить
 .
.
Отже, реальна кількість рівнів квантування сигналу згідно з виразом (9) буде
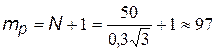 .
.
Таким чином, можна зробити висновок, що випадкові процеси є адекватною моделлю сигналів. Крім того безперервні сигнали допускають дискретне подання. На цій основі виникла теорія інформації, що розглядає сигнальну специфіку процесів.
Дата добавления: 2015-01-01; просмотров: 282; Мы поможем в написании вашей работы!; Нарушение авторских прав |