
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделирование очереди
| N | А | В | С | D | Е | F | G | Н |
Таким образом, при данных случайных наборах чисел в колонках A и В и покупателям приходилось стоять в очереди (колонка G), и продавцу - в ожидании покупателя (колонка H).
При моделировании систем такого вида возникают следующие вопросы. Какое среднее время приходится стоять в очереди к прилавку? Чтобы ответить на него, следует найти
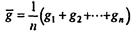
в некоторой серии испытаний. Аналогично можно найти среднее значение величины h. Конечно, эти выборочные средние сами по себе - случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки, не слишком отличающиеся друг от друга). Доверительные интервалы, в которых находятся точные средние значения (т.е. математические ожидания соответствующих случайных величин) при заданных доверительных вероятностях находятся методами математической статистики.
Сложнее ответить на вопрос, каково распределение случайных величин G и Н при заданных распределениях случайных величин А и В. Допустим, в простейшем моделировании мы примем гипотезу о равновероятных распределениях величин A и В - скажем, для А в диапазоне от 0 до 10 минут и В - от 0 до 5 минут. Для построения методом статистических испытаний распределений величин G и Н поступим так: найдем в достаточно длинной серии испытаний (реально - в десятках тысяч, что на компьютере делается достаточно быстро) значения gmax (для Н все делается аналогично) и разделим промежуток [0, gmax] на т равных частей - скажем, вначале на 10 - так, чтобы в каждую часть попало много значений gi. Разделив число попаданий nk в каждую из частей на общее число испытаний n, получим набор чисел pk = 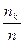 (k = 1, 2,...,n). Построенныепо ним гистограммы дают представление о функциях плотностей вероятности соответствующих распределений. По гистограмме можно составить представление о функции плотности распределения соответствующей случайной величины. Для проверки же гипотезы о принадлежности такого эмпирически найденного распределения тому или иному конкретному виду служат известные статистические критерии.
(k = 1, 2,...,n). Построенныепо ним гистограммы дают представление о функциях плотностей вероятности соответствующих распределений. По гистограмме можно составить представление о функции плотности распределения соответствующей случайной величины. Для проверки же гипотезы о принадлежности такого эмпирически найденного распределения тому или иному конкретному виду служат известные статистические критерии.
Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше т минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямой х = т и у = 0, к площади всей фигуры.
Приведем для сравнения результаты расчета средних значений величин g, h и соответствующих среднеквадратичных отклонений Sg, Sh, полученные при одинаковых значениях всех параметров в пяти разных сериях испытании по 10000 событий в серии (табл. 7.9) (входной поток покупателей - процесс равновероятных событий с максимальным временем между приходами 10 мин, длительность обслуживания также распределена равновероятным образом в интервале от 0 до 5мин).
Таблица 7.9
Дата добавления: 2015-01-01; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |