РАЗЛИЧНЫЕ ПРИМЕРЫ МОДЕЛИРОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

Метод статистического моделирования имеет множество приложений. Чаще всего он заключается в том, что для решения математической задачи строится некоторая случайная величина ζ, такая, что математическое ожидание этой случайной величины E(ζ) является значением искомого решения. Проводя достаточное количество раз эксперимент со случайной величиной ζ, можно найти приближенное решение как среднее значение результатов эксперимента.

1. Вычисление площадей. Найти площадь фигуры G, вписанной в прямоугольник с размерами сторон а и b. С помощью датчика равновероятно распределенных случайных чисел многократно генерируются координаты точки, принадлежащей прямоугольнику. Очевидно, что при большом числе испытаний площадь фигуры G приближенно равна отношению числа точек, попавших в область G, к числу всех разыгранных точек. В качестве примера приведем программу вычисления числа π, находя указанным методом площадь круга, вписанного в квадрат, по 100000 испытаний. Оценку точности полученного результата оставляем читателям.

Программа 154. Вычисление числа π методом Монте-Карло

Program Chislo_Pi;

Uses Crt; Var I, N : Longint; X, Y : Real;

Begin

Randomize; N := 0;

For I := 1 To 100000 Do

Begin

X := Random; Y := Random;

If Sqr(X - 0.5) + Sqr(Y - 0.5) < 0.25 Then N := N + 1

End;

WriteLn ('pi=', (N / 100000 / Sqr(0.5)) : 8 : 5) ;

Repeat Until KeyPressed End.

2. Задача Бюффона. На поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l (рис. 7.60). Какова вероятность того, что игла, упав, пересечег хотя бы одну прямую?

Рис. 7.60. К. задаче Бюффона

Ж.Бюффон (XVIII в.) подсчитал: р = 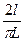. Таким образом, если L = 2l, то р = . Кроме того, р = , где N - число бросаний, N₁ - число пересечений иглы с линиями.

Относительная доля случаев, когда игла пересечет хотя бы однуиз параллельныхпрямых равно р = . Это был одиниз старинных способов опредения числа π.

Имитационное моделирование проведем следующим образом. Примем L = 1 и l = 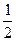. «Иглу» будем «бросать» в квадрат размером, скажем, 20х20, левый нижний угол которого имеет координаты (0, 0). Положение концов иглы будем задавать с помощью датчика равномерно распределенные, случайных чисел в диапазоне от 0 до 20. Точнее говоря, эти числа определят направление отрезка, вдоль которого находится очередная игла; для того, чтобы ее длина была равна 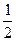, вторую из случайных точек - концов отрезка - подвинем вдоль него до достижения указанной длины иглы. В математическом отношении это сводится к следующей несложной процедуре;

• генерация координат точек А(х₁, y₁), B(x₂, у₂);

• определение координат точки В₁(х₁ + α(х₂ – х₁), у₁ + α(у₂ – у₁)), где

Поскольку расстояние между горизонтальными линиями взято равным единице, а сами линии имеют целочисленные координаты по у, то определить, пересекает ли игла прямую, очень просто - да, если целые части ординат тoчeк A и В₁ различны.

Программа 155 Решение задачи Бюффона.

Program Buffon;

Uses Crt; Var I, J, K, M, N : Integer; XI, X2, Y1, Y2, Al : Real;

Begin

Randomize; M := 30000; N := 1;

For I := 1 To M Do

Begin

X1 := Random * 20; Yl := Random * 20; X2 := Random * 20;

Y2 := Random * 20;

A1 := 0.5 / Sqrt(Sqr(X2 – X1) + Sqr(Y2 - Yl) ) ;

J := Round(Yl); К := Round(Yl + A1 * (Y2 – Y1));

If J <> К Then N := H + 1

End;

WriteLn('pi=', W / N) : 8 : 5); Repeat Until KeyPressed

End.

Создание демонстрационной программы, которая выводит на экран несколько параллельных прямых из общего набора и имеющие к ним отношение «иглы», предоставляем читателю.

Рекомендуем провести с предложенной программой несколько экспериментов. Понятно, что чем больше значение т, тем, по-видимому, точнее результат. Однако. почему он постоянно слегка занижен? Все ли учтено на краях той зоны, в которой разыгрываются броски иглы? Чтобы почувствовать проблему, следует увеличить число параллельных прямых, что в данной программе очень легко сделать. Почему результат становится лучше? Отметим, что проблема краевых условий, когда события должны по условиям задачи разыгрываться на бесконечном поле, а при имитационном моделировании фактически разыгрываются на конечном (и даже не очень большом), возникает часто и решение ее нетривиально.

3. Нефтяное месторождение. Дано нефтяное месторождение, в котором область залегания нефти G ограничивается кривой С. Дебит скважины, т.е. количество получаемой из нее нефти в единицу времени, зависит от пластового давления нефти U в точке скважины. Поэтом) для прогнозирования нефтедобычи важно знать распределение пластового давления на всем месторождении при условии, что оно экспериментально измерено лишь на его границе. В математическом плане функция U(r) удовлетворяет уравнению Лапласа = 0; задача нахождения его решения внутри области при заданном значении U(r) на границе - так называемая, краевая задача Дирихле; в данной задаче это решение, которое часто совсем не просто найти аналитически, позволило бы правильно определить точку для скважины.

Рис. 7.61. Наложение сетки на заданную область

Покроем область G мелкой сеткой. Отметим узлы, наиболее близкие к границе С, и будем считать, что значения функции U в этих узлах приблизительно равны значениям этой функции в ближайших к ним точках границы. Будем искать значение функции U(A) в некотором внутреннем узле A (рис. 7.61).

Поместим в точке А блуждающую частицу, которая может перемещаться по области в последовательные моменты времени, переходя из одного угла в соседний. Направления перемещений случайны, равновероятны и не зависят от ее положения и предыстории блуждания. Случайный эксперимент состоит в наблюдении факта выхода блуждающей частицы в некоторый граничный узел. Когда блуждание прекращается, запоминается значение функции f(с_i) в этой точке, и так далее, N раз. Замечательный факт состоит в том, что решение в точке

Другими словами, среднее значение приближенно равно решению задачи Дирихле в точке А.

4. Модель «пьяницы» (модель случайного блуждания). Зададим блуждание точки (объекта) по горизонтальной линии по правилу: если случайное число из интервала [0, 1] меньше 0,5, то точка делает шаг вправо x = х + h, в противном случае x = х - h.

Программа 156. Модель случайного блуждания

Program Tochka;

Uses Crt, Graph; Var I, J : Integer; Z, P, X, H, Y : Integer;

Begin

X := 320; Y := 240; H := 10; P := 4; DetectGraph(I, J) ;

InitGraphd, J, ");

SetColor(15); Line(10, 312, 630, 312); Randomize;

Repeat

Z := Random(8); If Z >= P Then X := X + H Else X := X - H;

SetColor(Green); Circle(X, Y, 10); Delay(200);

SetColor(0); Circle(X, Y, 10)

Until KeyPressed Or (X >= 640) Or (X <= 0); CloseGraph

End.

В программе шаг является постоянным, но никто не мешает нам сделать его переменным, выбирая из интервала [0, hmax] случайным образом. Для этого зададим максимально возможный шаг НМах и в цикле определимH := Random(HMax).

Если задать аналогичным образом вероятности движения точки вверх – вниз, вправо - влево (0 < рх < 1, 0 < рy < 1), получим хаотическое блуждание точки на плоскости. Для моделирования блуждания точки в замкнутом прямоугольном объеме примем абсолютно упругое (зеркальное) отражение от стенок.

Программа 157. Хаотическое блуждание точки

Program Broun;

Uses Crt, Graph;

Var I, J, X, Y, HxMax, HyMax, Hx, Ну : Integer; PI, P2, Z1, Z2 : Real;

Begin

X := 320; Y :== 240; HxMax := 30; PI := 0.5; P2 := 0.5; HyMax := 30;

DetectGraph (I, J) ; InitGraph (1, J, ''); SetColor(15);

Randomize; RectAngle(100, 100, 540, 380);

SetColor(Green); Circle(X, Y, 10); Delay(200); SetColor(0);

Circle(X, У, 10);

Repeat

Zl := Random; Z2 := Random; Hx := Random(HxMax);

Ну := Random(HyMax) ;

If (Zl < PI) Then X := X + Hx Else X := X - Hx;

If (Z2 < P2) Then Y := Y + Ну Else Y :" У - Ну;

If X <= 110 Then X := X + 2 * (110 - X) ;

If X >= 530 Then X := X - 2 * (-530 + X) ;

If Y <= 110 Then Y := Y + 2 * (110 - Y) ;

If Y >= 370 Then Y := Y - 2 * (Y - 370);

SetColor(Green); Circle(X, Y, 10); Delay(100);

SetColor(0); Circle(X, Y, 10)

Until Keypressed; CloseGraph

End.

Подобным (хотя и более сложным) образом происходит броуновское движение, хорошо известное из курса физики. Если след точки не стирать, то можно будет наблюдать на экране траекторию такого движения. Нет большого труда перейти к случаю п частиц. Для этого необходимо завести два массива координат точек и аналогично предыдущему примеру организовать их движение.

Программа 158. Броуновское движение

Program Gaz;

Uses Crt, Graph;

Var I, J, HxMax, HyMax, Hx, Ну, N, I : Integer;

X, Y : Array[0..500] Of Integer; PI, P2, Z1, Z2 : Real;

Begin N := 100;

For I := 1 To N Do Begin X[I] := 320; Y[I] := 240 End;

HxMax := 10; PI := 0.5; P2 := 0.5; HyMax := 10;

DetectGraph (1, J) ; InitGraphd, J, ' '); SetColor(15);

Randomize; RectAngle(100, 100, 540, 380);

For I := 1 To N Do PutPixel(X[I], Y[I], White); Delay(200);

For I := 1 To N Do PutPixel(X(I], Y[I], 0) ;

Repeat

For I := 1 To N Do

Begin

Zl := Random; Z2 := Random;

Hx := Random(HxMax); Ну := Random(HyMax);

If Zl < PI Then X[I] := X[I] + Hx Else X[I] := X[I]— Hx;

If Z2 < P2 Then Y[I] := Y[I] + Ну Else Y[I] := Y[I] - Ну;

If X[I] <= 110 Then X[I] := X[I] + 2 * (110 - X[I]);

If X(I] >= 530 Then X[I] := X[I] - 2 * (-530 + Х[I];

If Y[I] <= 110 Then Y(I] := Y[I] + 2 * (110 - Y[I]);

If Y[I] >= 370 Then Y[I] := Y[I] - 2 * (Y[I] - 370);

PutPixel (X[I], Y[I], 15)

End; Delay(100);

For I := 1 To N Do PutPixel(X[I], Y[I], 0)

Until KeyPressed; CloseGraph

End.

Построенная компьютерная модель в первом приближении может позволить моделировать многие явления и процессы, происходящие в газах: рассеивание облака, диффузия газов. С ее помощью можно получить многие зависимости параметров газа друг от друга. В частности, давление (число соударений частиц на стенки) от длины свободного пробега (величинHxMaxиHyMax) или от числа частиц.

Представляет значительный интерес имитационное моделирование явлений в сплошных средах, удовлетворяющих законам идеального газа, таких, как истечение газа в вакуум, ударная волна, волны разрежения и т.п. Для модернизации модели можно ввести в алгоритм упругое столкновение частиц друг с другом, возникновение кластерных ансамблей и многое другое.

При вероятностном моделировании используютразличные методы, которыепозволяют решать задачи из различных областей. Ниже перечислены сферы применения вероятностных методов.

Метод статистического моделирования: решение краевых задач математической физики, решение систем линейных алгебраических уравнений, обращение матриц и сводящиеся к ним сеточные методы решения систем дифференциальных уравнений, вычисление кратных интегралов, решение интегральных и интегродифференциальных уравнений, задач ядерной физики, газовой динамики, фильтрации, теплотехники.

Метод имитационного моделирования: моделирование систем массового обслуживания, задачи АСУ, АСУП и АСУТП, задачи защиты информации, моделирование сложных игровых ситуаций и динамических систем.

Метод стохастической аппроксимации: рекуррентные алгоритмы решения задач статистического оценивания.

Метод случайного поиска: решение задач оптимизации систем, зависящих от большого числа параметров, нахождение экстремумов функции большого числа переменных.

Другие методы: вероятностные методы распознавания образов, модели адаптации, обучения и самообучения.