Вихревой характер магнитного поля

Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей

Дивергенция электростатического поля не равна нулю в области источников. Силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных. Дивергенция магнитного поля везде равна нулю. Магнитные силовые линии вне источников магнитного поля замкнуты (в области источников поля вообще не имеют смысла). Ротор электростатического поля, как и его циркуляция, тождественно равен нулю. В любой точке вектор напряженности электростатического поля выражается через градиент некоторой скалярной функции, называемой потенциалом. Электростатическое поле потенциально. Ротор Вне равен нулю в области источников. Из-за этого и циркуляция Вне равна нулю в этой области. Вектор Вне является градиентом никакой скалярной функции координат. Магнитное поле, таким образом, непотенциально (является вихревым). В дальнейшем будет установлено, что электростатическое и магнитное поля представляют собой две стороны одной и той же объективной реальности – электромагнитного поля, которое, таким образом, в общем случае, содержит потенциальную и вихревую составляющие.

Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная:

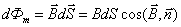
Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)

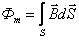
Магнитный поток - величина скалярная.

Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность.

Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:

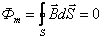
Это теорема Остроградского-Гаусса для магнитного поля.

Она свидетельствует о том, что в природе не существует магнитных зарядов – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции.

23

Зако́н Ампе́ра —закон взаимодействия электрических токов.

Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:

.

Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :

Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

где — угол между векторами магнитной индукции и тока.

Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ( ):

Работа сил магнитного поля

Элементарная работа А, совершаемая силой Ампера d Апри малом перемещении d 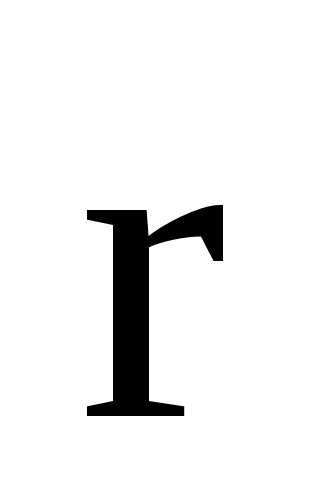в магнитном поле элемента тока Id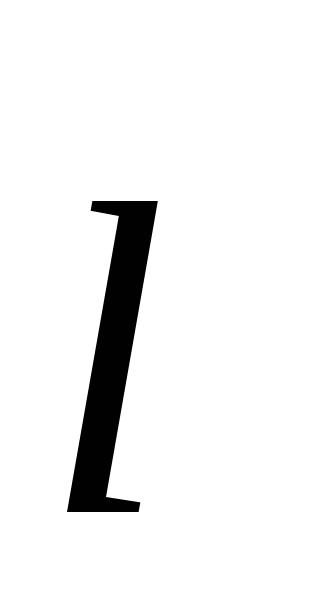
A = 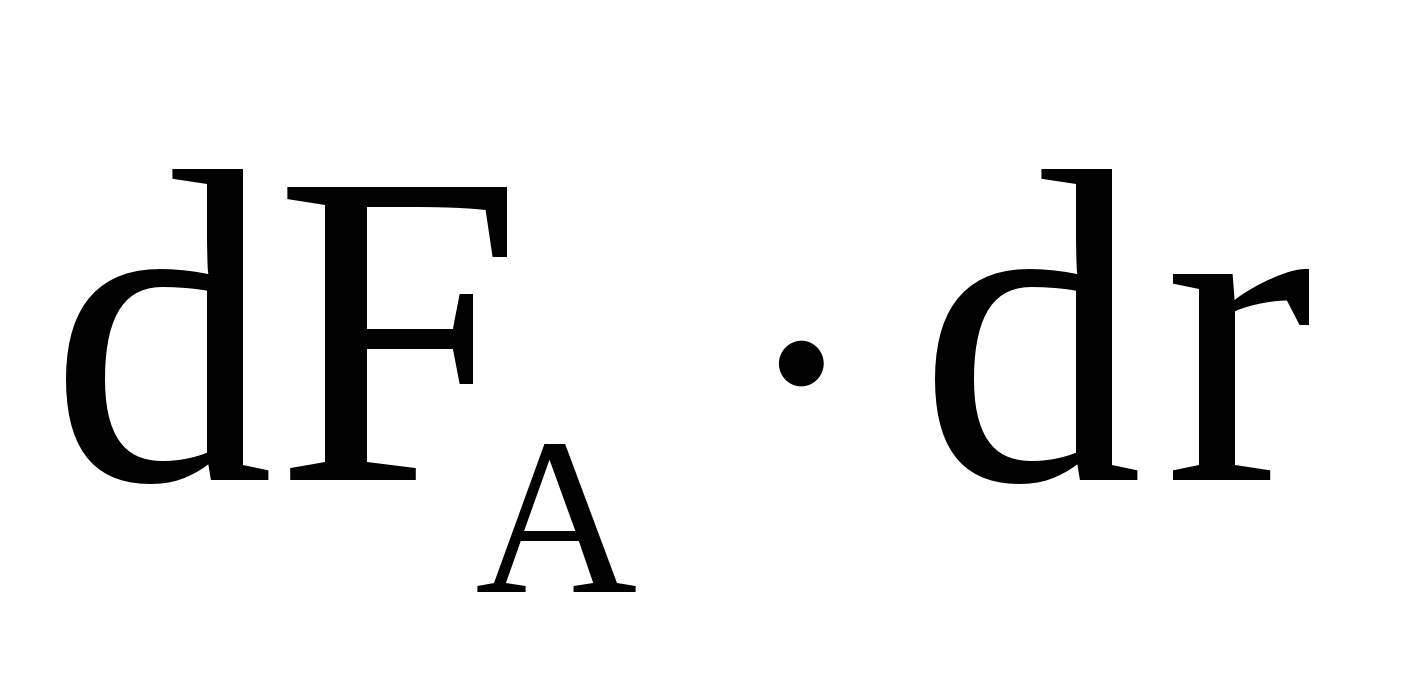= = 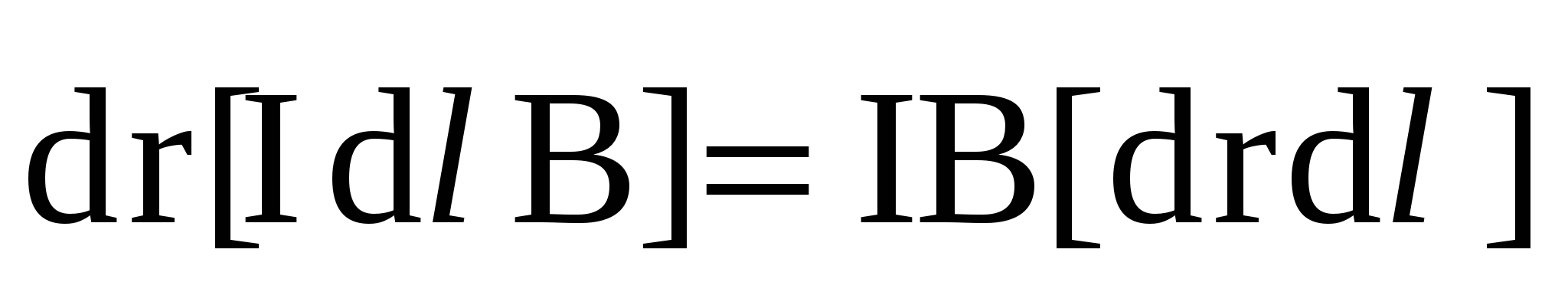= I dm

где dmмагнитный поток сквозь поверхность, которую прочерчивает элемент проводника при его перемещении.

Работа перемещения проводника с токомв постоянном магнитном поле

A = I∙m,

где Fm–магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его полном перемещении.

Работапри перемещении в магнитном полезамкнутого контура с постоянным током I из положения 1 в положение 2

A12= I (Фm2–Фm1) =Im,

где Фm1и Фm2–магнитные потоки через поверхность контура с током в начальном и конечном положениях.

Если в магнитном поле перемещается катушка, имеющая N витков, то работа может быть определена

A12= I12= INФm12

24.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле течёт электрический ток под действием напряжённости . Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости[1] будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов не скомпенсирует магнитную составляющую силы Лоренца:

Скорость электронов можно выразить через плотность тока:

где — концентрация носителей заряда. Тогда

Коэффициент пропорциональности между и называется коэффициентом (или константой) Холла

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечнуюзаряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического и магнитного полей. В Международной системе единиц (СИ) выражается как:

Сила F, действующая на частицу с электрическим зарядом q, движущуюся со скоростью v, во внешнем электрическом E и магнитном B полях, такова:

где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:

где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.

Непрерывное распределение заряда[править | править исходный текст]

Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока Jсоответствует движению заряженного элемента dq в объемеdV .

Для непрерывного распределения заряда, сила Лоренца принимает вид:

где dF — сила, действующая на маленький элемент dq.

25