Намагничение магнетика

Если несущие ток провода находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле В, которое накладывается на обусловленное токами поле Во. Оба поля в сумме дают результирующее поле

Намагничение магнетика естественно характеризовать магнитным моментом единицы объема. Эту величину называют намагниченностью и обозначают буквой J.

Если магнетик намагничен неоднородно, намагниченность в данной точке определяется следующим выражением:

где — физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, — магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заклкь ченным в объеме (ср. с формулой (16.1)).

Поле В, так же как и поле не имеет источников. Поэтому дивергенция результирующего поля (51.1) равна нулю:

26

1) Каждый движущийся по орбите электрон образует круговой ток силы , – частота обращения электрона вокруг ядра. Поскольку заряд электрона отрицательный, направление тока и направление движения электрона противоположны. Магнитный момент создаваемого электроном тока по величине равен:

,

где 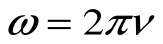– угловая скорость; r – радиус орбиты электрона.

Магнитный момент создается движением электрона по орбите, вследствие чего он получил название орбитального магнитного моментаэлектрона. Вектор образует с вектором орбитальной скорости электрона левовинтовую систему.

Движущийся по орбите электрон обладает моментом импульса, называемым орбитальным механическим моментомэлектрона:

.

Вектор образует с вектором скорости правовинтовую систему. Следовательно, направления векторов и противоположны.

Отношение магнитного момента элементарной частицы к ее механическому моменту называется гиромагнитным отношениемГ. Для орбитального движения электрона это отношение составляет:

.

Позже, в опытах Эйнштейна-де Гааза (Einstein A., 1879-1955; Haas A., 1884-1941) и Барнетта (Barnett S., 1873-1956), выяснилось, что наряду с орбитальными моментами, электрон обладает также собственным механическим моментом (спином) и собственным магнитным моментом , для которых гиромагнитное отношение оказалось в два раза большим:

.

Магнитный момент атома слагается из орбитальных и собственных магнитных моментов входящих в его состав электронов, а также магнитного момента ядра атома. Магнитный момент ядра, обусловленный магнитными моментами входящих в состав ядра протонов и нейтронов, значительно меньше электронных магнитных моментов, поэтому при рассмотрении многих вопросов им можно пренебречь. Таким образом, полный магнитный момент атома равен векторной сумме магнитных моментов всех его электронов.

Магнитный момент молекулы также можно считать равным сумме магнитныхмоментов входящих в ее состав электронов.

2)

Диамагнетизм — один из видов магнетизма, который проявляется в намагничивании вещества навстречу направлению действующего на него внешнего магнитного поля.

Диамагнетизм свойствен всем веществам. Диамагнетизм можно рассматривать как следствие индукционных токов, наводимых в заполненных электронных оболочках ионов внешним магнитным полем. Эти токи создают в каждом атоме индуцированный магнитный момент, направленный, согласно правилу Ленца, навстречу внешнему полю (независимо от того, имелся ли первоначально собственный момент или нет и как он был ориентирован).

27