Аксиомы статики

Аксиомы статики – это законы, установленные непосредственными наблюдениями и опытной проверкой следствий, логически вытекающих из аксиом.

Аксиома 1.Система двух сил, действующих на свободное твердое тело, является уравновешенной тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны.

На рис. 1.2 показаны две уравновешенные системы сил:

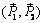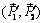~ 0; ~ 0.

Аксиома 1 дает необходимые и достаточные условия уравновешенности системы двух сил, две следующие аксиомы устанавливают простейшие операции, приводящие к эквивалентным системам сил.

Аксиома 2. Если к данной системе сил добавить или отнять от нее уравновешенную систему сил, то полученная система сил будет эквивалентна исходной.

Из этой аксиомы вытекает следствие: «Действие силы на твердое тело не изменится, если перенести точку приложения силы вдоль линии ее действия».

Для доказательства следствия рассмотрим силу 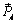, приложенную в точке A (рис. 1.3,а). В точке B на линии действия силы приложим уравновешенную систему сил 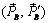, где . Тогда в соответствии с аксиомой 2 получим 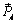~ 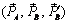(рис. 1.3,б). Согласно аксиоме 1 система сил 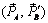~ 0, а согласно аксиоме 2 их можно отбросить (рис. 1.3,в), т.е. 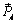~ ~ 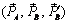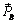, что и доказывает следствие.

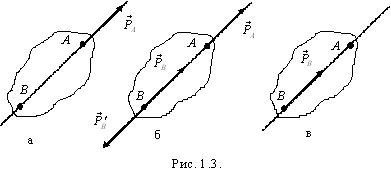
Таким образом, сила, приложенная к абсолютно твердому телу, является скользящим вектором.

Аксиома 3(аксиома параллелограмма сил). Система двух сил, приложенных к телу в одной точке, имеет равнодействующую, приложенную в той же точке и равную геометрической сумме сил.

Эта аксиома не только устанавливает существование равнодействующей рассматриваемой системы сил ~ 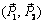(рис. 1.4), но и дает правило ее определения: 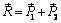. Модуль равнодействующей

.

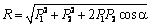Аксиома 4(3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

Силы взаимодействия двух тел удовлетворяют всем условиям аксиомы 1, кроме одного – они приложены к разным телам (рис. 1.5), и поэтому не образуют уравновешенную систему сил.

Аксиома 5(принцип отвердевания). Равновесие изменяемого (деформируемого) тела не нарушится, если тело станет абсолютно твердым.

Другими словами, при равновесии деформируемого тела силы, действующие на него, удовлетворяют тем же условиям, что и для абсолютно твердого тела, но эти условия для деформируемого тела будут только необходимыми, не являясь достаточными.

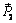Рассмотрим в качестве примера деформируемого тела нить, которая находится в равновесии под действием двух сил и , приложенных к ее концам, как показано на рис. 1.6,а. В соответствии с аксиомой 1 эти силы должны действовать вдоль одной прямой (вдоль нити) в противоположные стороны и иметь одинаковые модули. Для того, чтобы эти условия стали достаточными, к ним следует добавить еще одно: силы, действующие на нить, должны быть растягивающими. При тех же условиях абсолютно твердое тело – стержень (рис. 1.6,б) будет находиться в равновесии под действием как растягивающих, так и сжимающих сил.

32

Сложение двух сил. Сложение трех сил, не лежащих в одной плоскости. Сло­жение системы сил.Понятие о геом сумме сил не следует смешивать с понятием о равнодействующей, поскольку не всегда есть равнодействующая.

^ Сложение 2х сил. Геом сумма 2х сил F₁ и F₂ находится по правилу пар-ма или построением силового треугольника. # Сложение 3х сил, не лежащих в одной пл-ти – геом сумма сил F₁,F₂, F₃ не лежащих в одной пл-ти изображается диагональю параллелепипеда, построенного на этих силах.