Разложение сил.

Разложить данную силу на несколько составляющих значит найти такую систему сил, для к-й данная сила является равнодействующей.

Система сил, линии действия которых пе­ресекаются в одной точке, называется сходя­щейся (рис. 2.1).

Необходимо определить равнодействую­щую системы сходящихся сил (F1; F2; F3; …; Fn), n — число сил, входящих в систему. игровые автоматы играть бесплатно

По следствию из аксиом статики, все си­лы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.

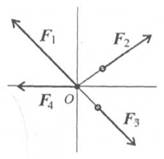
Рис. 2.1

Равнодействующая сходящихся сил

Равнодействующую двух пересекающихся сил можно опреде­лить с помощью параллелограмма или треугольника сил (4-я ак­сиома) (рис. 2.2).

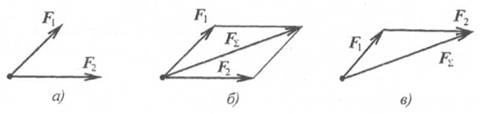
Рис. 2.2

Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.

При графическом способе определения равнодействующей век­торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

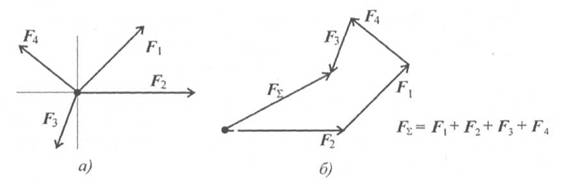
Рис. 2.3

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.

33

Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей:

· Тело отсчета;

· Систему измерения положения тела в пространстве (систему координат);

· Прибор для измерения времени (Часы).

Положение точки определяется набором обобщенных координат — упорядоченным набором числовых величин, полностью описывающих положение тела. В самом простом случае это координаты точки (радиус-вектора) в выбранной системе координат. Наиболее наглядное представление о радиус-векторе можно получить вевклидовой системе координат, поскольку базис в ней является фиксированным и общим для любого положения тела.

34

К простейшим движениям твердого тела относятся поступательное и вращательное.

Поступательным называется движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному положению.

Теорема. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют в каждый момент времени равные скорости и ускорения.

Вращательным называется движение твердого тела, при котором все точки некоторой прямой, связанной с телом, остаются неподвижными во время движения. Эта прямая называется осью вращения.

(рис. 2.2.1)

Положение тела определено, если задан угол между плоскостями и , проходящими через ось вращения ( с единичным направляющим вектором ) (рис. 2.2.1) . Плоскость неподвижна, а плоскость жестко связана с телом. Угол измеряется в радианах и изменяется с течением времени, 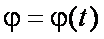– уравнение вращательного движения твердого тела.

Угловая скорость характеризует изменение угла поворота с течением времени.

Угловое ускорение – характеризует быстроту изменения угловой скорости.

Если угловая скорость постоянна, то вращение называется равномерным и происходит по закону .

Если угловое ускорение постоянно, то вращение называется равнопеременным и происходит согласно уравнениям:

, .

Модули скорости, ускорения, касательного, нормального ускорений точки вращающегося тела, находящейся на расстоянии от оси вращения, определяются по формулам:

… …

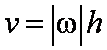
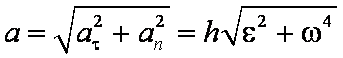Ускорение точки составляет угол с направлением нормали, при этом

35

Динамика — раздел теоретической механики, в котором уста­навливается связь между движением тел и действующими на них силами.

В динамике решают два типа задач:

• 
  определяют параметры движения по заданным силам;
• 
  определяют силы, действующие на тело, по заданным кине­матическим параметрам движения.

При поступательном движении все точки тела движутся одина­ково, поэтому тело можно принять за материальную точку.

Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.

При вращательном движении тела точки могут двигаться не­одинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рас­сматривать как совокупность материальных точек.

Поэтому динамику делят на динамику точки и динамику материальной системы.