КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и , четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой.
Первая аксиома (принцип инерции)
Всякая изолированная материальная точка находится в стоянии покоя или равномерного и прямолинейного движения, приложенные силы не выведут ее изэтого состояния.
Это состояние называют состоянием инерции. Вывести из этого состояния, т.е. сообщить ей некоторое ускорение, внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома(второй закон Ньютона — основной закон динамики)
Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая:
F = та,
где т — масса точки, кг; а— ускорение точки, м/с2.
Ускорение, сообщенное материальной точке силой, nponoрционально величине силы и совпадает с направлением силы.
Основной закон динамики в дифференциальной форме:
На все тепа на Земле действует сила тяжести, она телу ускорение свободного падения, направленное к центру Земли:
G = mg,
где g = 9,81 м/с2, ускорение свободного падения.
Третья аксиома (третий закон Ньютона) Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны (рис. 13.1):
При взаимодействии ускорения обратно пропорциональны массам.
Четвертая аксиома(закон независимости действия сип) Каждая сила системы сил действует так, как она действовала бы одна.
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности.
36
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
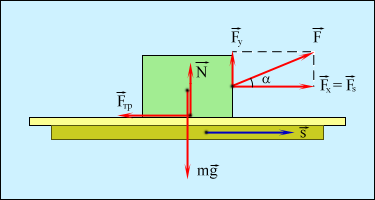
Работой A, совершаемой постоянной силой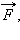 
называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы 
и перемещения 
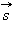(рис. 1.18.1):
|
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
|
| Рисунок 1.18.1.
Работа силы : A = Fs cos α = Fss.
|
Если проекция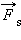 
силы на направление перемещения 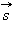не остается постоянной, работу следует вычислять для малых перемещений Δsi и суммировать результаты:
|
Это сумма в пределе (Δsi → 0) переходит в интеграл.
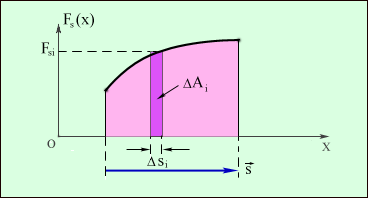
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 1.18.2).
|
| Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi. |
Примером силы, модуль которой зависит от координаты, может служить упругая сила пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу 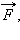модуль которой пропорционален удлинению пружины (рис. 1.18.3).
|
Рисунок 1.18.3.
Растянутая пружина. Направление внешней силы совпадает с направлением перемещения 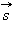. F = Fs = kx, k – жесткость пружины. 
|
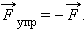
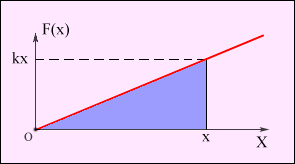
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).
|
| Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины. |
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
|
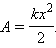
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы 
равна по модулю работе внешней силы и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами и равна работе равнодействующей приложенных сил.
|
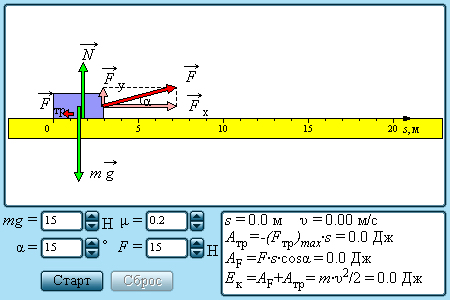
| Модель. Механическая работа. |
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
|
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
|
Дата добавления: 2015-01-01; просмотров: 664; Мы поможем в написании вашей работы!; Нарушение авторских прав |