Моделі потоків

Функціонування складних систем пов’язано з деякою подією, тобто з переходом з одного стану в інший у деякі моменти часу.

Назвемо потоком подій послідовність однорідних подій, що відбуваються одна за одною у довільні моменти часу. Потік подій наочно зображується послідовністю точок на осі часу (рис. 3).

Рис. 3. Потік подій

Щільністю (інтенсивністю) потоку називають середню кількість подій в одиницю часу.

Потік подій називають ординарним, якщо ймовірність появи на елементарному відрізку часу двох і більше подій мала порівняно з імовірністю появи однієї події. Інтервали ординарного потоку можуть бути однаковими і різними, дискретними і безперервними, випадковими і невипадковими. Якщо інтервали невипадкові, то потік подій є регулярним, або детермінованим, і повністю характеризується конкретними значеннями . Якщо інтервали випадкові, то потік подій є випадковим і повністю вичерпується спільним законом розподілу .

Якщо величини є залежними випадковими, то потік називають потоком з післядією, тому що для будь-якого моменту часу наступне значення потоку знаходиться в імовірнісній залежності від попередньої події. Якщо величини є незалежними, то випадковий потік називають потоком без післядії.

Як приклад розглянемо ординарний потік подій без післядії – пуасонівський потік. Якщо події утворюють пуасонівський потік, то кількість подій, що потрапляють на будь-який відрізок часу , розподіляється за законом Пуассона

, (1)

де а – математичне сподівання кількості точок, які потрапили на відрізок часу,

. (2)

Тут – щільність потоку.

Якщо , то пуасонівський потік називають стаціонарним пуасонівським потоком, або найпростішим потоком. Для цього потоку кількість подій, що потрапляють на будь-який відрізок часу, розподіляється за законом Пуассона з параметром

. (3)

Відстань Т між двома сусідніми подіями в найпростішому потоці є безперервною випадковою величиною, розподіленою за показовим законом з щільністю

Для випадкової величини Т, розподіленої за показовим законом,

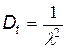, . (4)