
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Загальні підходи до аналізу динамічних ТС
Методи структурного аналізу дають можливість моделювати поводження тільки статичних ТС або оцінювати топологічні особливості динамічних ТС. Як уже зазначалося раніше, правила дослідження динамічних ТС визначаються відповідно до функціонального опису, де базовими поняттями є поняття стану і поводження.
Функціонування багатьох ТС являє собою послідовність переходів з одного стану в інший. При такому формалізованому зображені процесу функціонування ТС вивчення її характеристик зводиться до вивчення абстрактного процесу переходів з одного стану в інший у межах повної множини станів.
| Приклад | Функціонування комп'ютера характеризується тим, що в кожний момент часу оброблення вхідної інформації реалізується певними його блоками, причому всі блоки функціонують з визначеною тактовою частотою. Тому процес дискретного оброблення інформації можна розглядати як процес переходів ТС з одних станів в інші. |
Нехай є деяка ТС  , яка у процесі функціонування може набувати різних станів
, яка у процесі функціонування може набувати різних станів 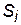 (
( 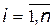 ). При цьому ТС перебуває в деякому стані
). При цьому ТС перебуває в деякому стані 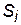 , якщо вона повністю описується значеннями змінних, які визначають цей стан, тобто стан
, якщо вона повністю описується значеннями змінних, які визначають цей стан, тобто стан 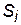 визначається величиною
визначається величиною
 ,
,
де  – момент часу;
– момент часу;  – випадкова величина, що характеризує стан ТС в момент часу
– випадкова величина, що характеризує стан ТС в момент часу  ;
; 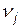 (
(  ) – властивість ТС, що описує поточний стан;
) – властивість ТС, що описує поточний стан;  – кількість властивостей ТС, необхідних для визначення стану
– кількість властивостей ТС, необхідних для визначення стану 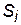
Система переходить з одного стану в інший, якщо значення змінних 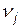 , що задають цей стан, змінюються на інші, які задають інший стан. Якщо стани системи змінюються в часі випадковим образом, то їхню послідовність можна розглядати як випадковий процес, тобто набір випадкових величин {
, що задають цей стан, змінюються на інші, які задають інший стан. Якщо стани системи змінюються в часі випадковим образом, то їхню послідовність можна розглядати як випадковий процес, тобто набір випадкових величин {  } (
} ( 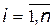 ) утворює випадковий (стохастичний) процес.
) утворює випадковий (стохастичний) процес.
| Приклад | Процеси відмов і відновлень у радіотехніці є випадковими процесами; процеси надходження заявок на обслуговування в комп'ютерних мережах, процеси керування за наявності перешкод у системі керування також є випадковими процесами. Протікання кожного з розглянутих процесів залежить від багатьох випадкових, заздалегідь непередбачуваних факторів. |
Неважко помітити, що основними поняттями випадкового процесу є стани ТС і переходи з одного стану в інший. Відповідно до цього класифікацію ТС з випадковими процесами наведено на рис. 1.

Рис. 1. Класифікація динамічних систем з випадковими процесами
Якщо множина станів ТС необмежена, а їхня зміна характеризується поступовими, плавними переходами зі стану в стан, то процес, що відбувається в системі, є випадковим процесом з безперервними станами. ТС називають системою з дискретними станами, якщо множина її станів скінченна, а переходи з одного стану в інший здійснюються стрибком. Послідовність станів такої системи, тобто випадковий процес переходів зі стану в стан, називають ланцюгом. Далі будемо розглядати тільки такі ТС.
Інтервал між двома послідовними переходами ТС зі стану 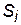 у стан
у стан  і зі стану
і зі стану  у
у 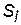 , тобто час перебування системи в деякому стані
, тобто час перебування системи в деякому стані  , може бути дискретною або безперервною змінною величиною. Залежно від цього розрізняють ТС і випадкові процеси з безперервним і дискретним часом. У системах з дискретним часом перехід може здійснюватися в строго заздалегідь визначені фіксовані моменти часу; у системах з безперервним часом перехід з одного стану в інший здійснюється в будь-який час. Інтервали між суміжними моментами переходів називають кроками (етапами).
, може бути дискретною або безперервною змінною величиною. Залежно від цього розрізняють ТС і випадкові процеси з безперервним і дискретним часом. У системах з дискретним часом перехід може здійснюватися в строго заздалегідь визначені фіксовані моменти часу; у системах з безперервним часом перехід з одного стану в інший здійснюється в будь-який час. Інтервали між суміжними моментами переходів називають кроками (етапами).
| Приклад | Типовими процесами з дискретними станами є процеси, що описують функціонування ЕОМ, роботу АТС тощо; процесами з безперервними станами можна вважати процес зміни напруги в освітлювальній мережі, просторову орієнтацію супутника й т.д. Як процес із дискретним часом можна розглядати процес зміни станів запам'ятовувального пристрою ЕОМ. Однак зазначимо, що більшість випадкових процесів, що відбуваються у реальних ТС, є процесами з безперервним часом, а саме: відмова будь-якого елемента апаратури, відновлення цього елемента й т.д. |
Найпростіша ймовірнісна характеристика випадкового процесу (ланцюга), – це набір ймовірностей станів 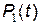 ,
, 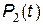 , …,
, …, 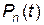 за умови, що
за умови, що
 , (1)
, (1)
де 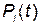 – імовірність того, що в момент часу
– імовірність того, що в момент часу  система перебуває в стані
система перебуває в стані 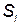 (
( 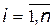 ).
).
Якщо в процесі функціонування система опинилася в стані 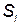 , то ймовірність переходу її з цього стану в стан
, то ймовірність переходу її з цього стану в стан  у загальному випадку відповідно до принципу причинності залежить не тільки від стану
у загальному випадку відповідно до принципу причинності залежить не тільки від стану 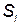 , але й від попередніх станів. Однак найбільш поширені ланцюги, що мають марківську властивість. Марківським (або процесом без післядії) називають процес, для якого має місце таке твердження: випадковий процес, що відбувається в ТС, є марківським, якщо для будь-якого моменту часу
, але й від попередніх станів. Однак найбільш поширені ланцюги, що мають марківську властивість. Марківським (або процесом без післядії) називають процес, для якого має місце таке твердження: випадковий процес, що відбувається в ТС, є марківським, якщо для будь-якого моменту часу 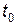 імовірність будь-якого стану ТС в майбутньому (
імовірність будь-якого стану ТС в майбутньому (  ) залежить тільки від її поточного стану (
) залежить тільки від її поточного стану ( 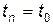 ) і не залежить від того, яким чином ТС перейшла в цей стан (тобто як процес розвивався в минулому).
) і не залежить від того, яким чином ТС перейшла в цей стан (тобто як процес розвивався в минулому).
Іншими словами, у марківському випадковому процесі майбутнє залежить тільки від поточного стану й не залежить від історії процесу, тобто для всіх значень випадкових величин  має місце вираз
має місце вираз
 , (2)
, (2)
де  – умовна ймовірність того, що система перебуває в стані
– умовна ймовірність того, що система перебуває в стані  у момент
у момент 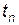 , якщо в момент
, якщо в момент  вона перебувала в стані
вона перебувала в стані 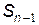 .
.
Як приклад аналізу динамічних ТС систем розглянемо приклад використання марківських моделей під час дослідження їх надійності (тобто властивості, що забезпечує можливість виконання системою заданих функцій з певними характеристиками протягом заданого інтервалу часу при певних експлуатаційних умовах). Є принаймні три істотні причини для прийняття марківської моделі в цьому випадку.
Справа в тому, що у першому наближенні опис більшості ТС і процесів у радіоелектроніці такий, що знання передісторії цих систем не має великої цінності для передбачення їхнього поводження у майбутньому. По-друге, складні ТС в будь-який момент часу можуть перебувати в одному з множини можливих станів. Кожен такий стан системи можна описати, вказавши множину працездатних елементів. У загальному випадку дискретна кількість станів складної ТС залежить від кількості елементів системи і можливої кількості станів кожного з них, тобто дослідити надійність ТС можна шляхом вивчення процесу переходів системи зі стану в стан. По-третє, якщо кожний з елементів ТС має хоча б приблизний експонентний розподіл наробітку на відмову, то поводження всієї системи можна описати випадковим процесом. Отже, випадковий марківський процес є адекватною ймовірною моделлю для такого типу процесів.
Марківськімоделі є потужним інструментом подання й дослідження складних ТС. Це зумовлено такими причинами:
- вони набули широкого застосування серед сучасних методів дослідження складних ТС систем, тому що є узагальненням математичної моделі системи з елементами, які функціонують незалежно;
- вони відносно прості й доступні широкому класу дослідників і, водночас дають можливість ураховувати залежність стану системи від її попереднього стану, що дуже важливо для дослідження динамічних ТС;
- використання марківських моделей дає можливість пояснити фізичний зміст процесів, що відбуваються у ТС.
Дата добавления: 2015-01-01; просмотров: 278; Мы поможем в написании вашей работы!; Нарушение авторских прав |