
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение (по какой траектории двигалась).
Траектория –линия, описываемая материальной точкой (или телом) при движении относительно выбранной системы отсчета.
Траектории одного и того же движения тела в разных системах отсчета могут быть различными.
В зависимости от формы траектории различают:
– прямолинейное движение,
– криволинейное движение,
– поступательное движение,
– вращательное движение.
Радиус-вектор и координаты
Положение материальной точки (·) М в пространстве в данный момент времени может быть задано радиусом-вектором  или тремя координатами x, y, z (Рис.3.1.).
или тремя координатами x, y, z (Рис.3.1.).
Радиусом-вектором  некоторой точки называется вектор, проведеный из начала координат в эту точку. Его проекции на координатные оси равны декартовым координатам данной точки:
некоторой точки называется вектор, проведеный из начала координат в эту точку. Его проекции на координатные оси равны декартовым координатам данной точки:
rx = x, ry = y, rz = z,
Следовательно, радиус вектор можно представить в виде
 ,
,
где  – единичные векторы (орты) соответствующих осей системы координат. Соответственно r2 = x2 + y2 + z2.
– единичные векторы (орты) соответствующих осей системы координат. Соответственно r2 = x2 + y2 + z2.
 |  |
При движении материальной точки ее координаты с течением времени изменяются (рис. 3.2). В общем случае ее движение определяется системой скалярных уравнений
 x = x(t),
x = x(t),
y = y(t),(1)
z = z(t),
эквивалентной векторному уравнению 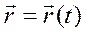 . (2)
. (2)
Уравнения (1) и (2) называют кинематическими уравнениями движения материальной точки.
Вектор перемещения  – вектор разности радиус-векторов конечного и начального положения движущейся точки за рассматриваемый промежуток времени Δt.
– вектор разности радиус-векторов конечного и начального положения движущейся точки за рассматриваемый промежуток времени Δt.
Длина пути ∆s – длина участка траектории AB, пройденного точкой за данный промежуток времени: ∆s = ∆s(t) – скалярная функция времени.
Дата добавления: 2015-01-05; просмотров: 223; Мы поможем в написании вашей работы!; Нарушение авторских прав |