
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
Скорость и ускорение при криволинейном движении
В случае криволинейного движения важно знать, как изменяется скорость не только по величине, но и по направлению. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.

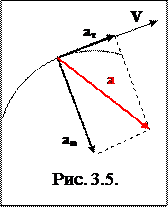
В общем случае плоского криволинейного движения вектор ускорения удобно представить в виде суммы двух его проекций:
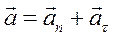
где: 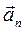 – нормальное ускорение (проекция вектора полного
– нормальное ускорение (проекция вектора полного
ускорения на радиус кривизны).
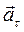 –тангенциальное (касательное) ускорение, направленное вдоль вектора скорости.
–тангенциальное (касательное) ускорение, направленное вдоль вектора скорости.
Рассмотрим плоское движение точки (Рис. 3.4.). Пусть скорость точки А в момент времени t равна V. За время Δt точка перешла в положение В и приобрела скорость, отличную от V как по модулю, так и по направлению и равную V1 = V + ΔV.
Средним ускорением неравномерного движения толчки в интервале времени от t до t + Δt называется векторная величина, равная отношению приращения скорости ΔVк интервалу времени Δt, за которое это приращение произошло:
аср = ΔV/ Δt
Мгновенным ускорением (ускорением) материальной точки в момент времени t является предел среднего ускорения:
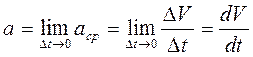
Тангенциальное ускорение – 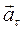 характеризует быстроту изменения модуля скорости. Модуль тангенциального ускорения определяется как
характеризует быстроту изменения модуля скорости. Модуль тангенциального ускорения определяется как
 и направлен по вектору скорости.
и направлен по вектору скорости.
Модуль нормального ускорения 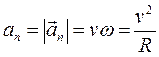 и направлен по радиусу к центру кривизны траектории в данной точке (Рис. 3.6.).
и направлен по радиусу к центру кривизны траектории в данной точке (Рис. 3.6.).
Кривизна траектории – 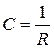 .
.
 |
Модуль вектора полного ускорения:
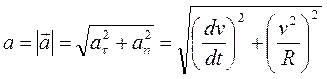 .
.
Частные случаи
В зависимости от соотношения тангенциальной и нормальной составляющих ускорения, движение можно классифицировать следующим образом:
1)  ,
, 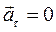 – прямолинейное равномерное движение;
– прямолинейное равномерное движение;
2)  ,
, 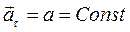 – прямолинейное равноускоренное
– прямолинейное равноускоренное
движение:
 , откуда скорость
, откуда скорость 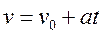 .
.
Длина пути за время t при прямолинейном равноускоренном движении:
 |
3)  ,
, 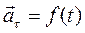 – прямолинейное движение с переменным ускорением;
– прямолинейное движение с переменным ускорением;
4) 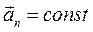 ,
, 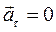 – равномерное движение по окружности;
– равномерное движение по окружности;
В данном случае скорость по модулю не изменяется, а изменяется по направлению. Из выражения  следует, что радиус кривизны остается постоянным. Это доказывает, что движение происходит по окружности.
следует, что радиус кривизны остается постоянным. Это доказывает, что движение происходит по окружности.
5)  ,
, 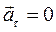 – равномерное криволинейное движение;
– равномерное криволинейное движение;
6)  ,
, 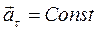 - равноускоренное криволинейное движение;
- равноускоренное криволинейное движение;
7)  ,
, 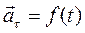 – криволинейное движение с переменным ускорением.
– криволинейное движение с переменным ускорением.
Дата добавления: 2015-01-05; просмотров: 321; Мы поможем в написании вашей работы!; Нарушение авторских прав |