ВЫПОЛНЕНИЕ И ЗАЩИТА

2.1. Схема включення, статичні характеристики і режими роботи асинхронного двигуна.

У результаті того, що фази розміщені геометрично по всій окружності обмотки статора, то в ньому створюється обертаюче магнітне поле зі швидкістю :

; .

Ротор двигуна являє собою замкнений вид обмотки. У результаті обертового поля в зазорі, наводиться ЕРС у роторі, тобто транспортується енергія зі статора в ротор. Якщо роторна обмотка замкнена, то в ній протікає струм . Взаємодія потоку зі струмом ротора створює момент.

Якщ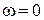о , то має максимальне значення, тобто 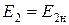; якщ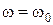о , то . Швидкість обертового поля статора чисельно дорівнює швидкості ідеального холостого ходу, тому часто швидкість статора називається синхронною. Таким чином, ідеальний холостий хід визначається, якщо 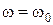. При цьому , а виходить, двигун обертається синхронно з обертовим полем статора. Двигун у такому режимі працювати не може, тому що отже . Асинхронний двигун працює, якщо або . Ковзання асинхронного двигуна:

.

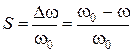12.2. Схема заміщення АД з винесеним контуром намагнічування має вигляд:

Приймемо:

- активний опір статора;

- активний опір ротора, приведений до обмотки статора.

- коефіцієнт трансформації двигуна.

Індуктивний опір короткого замикання:

Формула потужності:

,

де , - повний опір.

12.3. Рівняння електромеханічної характеристики АД.

.

Загальний коефіцієнт потужності:

Підставимо значення та у рівняння потужності, одержимо:

де: 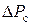- втрати в статорі;

- потужність, передана ротору.

Електромагнітний момент, що розвивається двигуном:

;

- механічна характеристика.

.

12.4. Формула Клосса

Електромагнітний момент АД є складною функцією ковзання, тому для знаходження максимального моменту необхідно взяти похідну від моменту по ковзанню і прирівняти її до нуля. Знайдемо критичне ковзання :

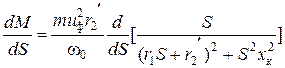
Примітка: .

У такий спосіб

З отриманого вираження визначимо ковзання, при якому момент має максимальне значення. Це ковзання називається критичним.

;

(+) – двигунний режим;

(-) – генераторний режим.

Щоб визначити критичний момент потрібно у формулу моменту підставити .

;

;

.

Момент змінюється по величині. При , підставляючи у формулу моменту, одержимо пусковий момент:

Розділимо на й одержимо:

.

( Чисельник і знаменник ділили на .)

Ця формула, у якій показана залежність моменту від відомих параметрів машини (формула Клосса):

.

Якщо говорити про природню характеристику, то виміряється в сотих долях. для двигунів середньої й великої потужності. У цьому випадку невраховують , тому що це відношення дуже мале. У результаті одержимо спрощену формулу Клосса:

( при ).

Проаналізуємо цю формулу. На одній ділянці, де 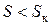, , 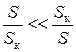значить можна записати .

Залежність моменту від ковзання – пряма лінія. На другій ділянці, де , , одержимо .

Двигун працює на прямолінійній ділянці. Нижня ділянка різна для двигунів з фазним ротором і для двигунів з короткозамкненим ротором (відбувається витиснення струму з ротора).

12.5. Побудова природньої характеристики АД

Для побудови природніх механічних характеристик АД слід застосовувати наближену формулу Клосса. Але необхідно ще знати і .

визначається за паспортним даними:

[ ].

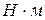Якщо у формулу Клосса замість підставити , а замість , то:

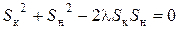
Вирішуючи це рівняння, одержуємо:

.

Негативний корінь не береться, тому що немає фізичного змісту. Таким чином, ми знаємо всі значення, і, задаючись ковзанням від 0 до 1, будуємо природню характеристику, яка слушна для двигуна з фазним ротором і короткозамкненим з “простій білячою обмоткою”.

12.6. Побудова штучних характеристик АД

(Характерні крапки)

Проаналізуємо характерні крапки механічної характеристики АД:

1 крапка: , , .

2 крапка: , , 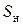- паспортні значення.

3 крапка: , , .

;

де 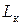- індуктивність К.З. визначається числом витків даного магнітопроводу і т.д.

- цим активним опором зневажаємо.

Перепад швидкості при критичному моменті:

.

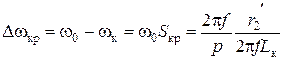
Момент у цій крапці рівний ( при ).

,

де .

4 крапка: , 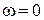. Це пускова крапка.

, де

; .

Становимо логічну таблицю:

	-			-	-
	-		-
	-	-
					-
		*		**	***

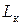
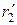
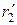
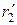
, - параметри мережі;

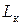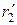, , - параметри двигуна.

* - нелінійно.

При (у знаменнику) величиною 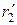невраховують, то . Якщо , то

** - нелінійно.

при

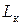не залежить від при .

*** - якщо знаменник невраховують і зі збільшенням 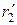момент пусковий росте ( ). Якщо , то невраховують величину і момент зі збільшенням 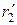зменшується.

ВЫПОЛНЕНИЕ И ЗАЩИТА

ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «КРИМИНАЛИСТИКА»