C) связный граф без циклов

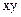
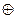
Полином Жегалкина для функции f(x, y) = 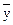имеет вид

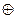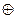D) 1 y xy

Является ли функция f(x, y), заданная таблицей

сохраняющей нуль, сохраняющей единицу, самодвойственной?

E) да нет нет

Какая из приведенных функций тождественно ложная?

D) a &

Сколько всевозможных подмножеств содержит множество А ={0, 2, 4, 6, 8, 10, 12, 14, 16, 18}?

A) 1024

Сколько существует всевозможных функциональных отображений множества А во множество В?

А ={1, 2, 3, 4} В={5, 6, 7}

C) 81

Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если каждая из них в числе встречается не более одного раза?

A) 720

Сколько элементов содержит множество А × В, если А ={1, 2, 3, 4} и В={3, 1, 5}?

D) 12

Из данного множества формул выделите ту, которая имеет вид конъюнктивной нормальной формы (КНФ)

B)

Найдите равные множества в данной последовательности:

1) (А \ В) ∩ С 2) (В \ А) ∩ С 3) (С \ В) ∩ А

A) 1 и 3

Сколько элементов содержит множество (В \ А) × А, если А ={1, 2, 3, 4, 5} В={3, 4, 5}?

A) 0

Пусть А – множество натуральных четных чисел; В – множество натуральных чисел, кратных трем. Найдите разность В \ А.