A) множество чисел, кратных шести

Найдите объединение множеств Х и Y (X Y), если X = {x | 1 £ x <3}, Y = {y | 2 £ y £ 4}

A) {x | 1 £ x £ 4}

Сколькими способами можно рассадить за столом президиума 6 человек?

E) 720

Чему равна мощность множества А = { 3, 5, 7, 9,12, 15}

E) 6

Какое их перечисленных множеств имеет мощность континуума?

B) множество всех иррациональных чисел

Укажите среди данного набора множеств пустое

C)

Из данного множества формул выделите ту, которая имеет вид дизъюнктивной нормальной формы

B)

Какая из функций тождественно истинная?

D)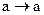

Дана матрица бинарного отношения

Является ли это отношение рефлексивным, симметричным, транзитивным?

C) нет, да, нет

Сколькими способами можно разбить множество из 5 объектов на 3 непустые части?

B) 25

Сколькими способами можно выбрать 5 разных газет из 6 наименований, имеющихся в продаже?

D) 6

Сколькими способами можно выбрать из группы в 6 человек троих на курсы по программированию?

E) 20

Сколькими способами можно выбрать 3 разных блюда в ресторане из семи, имеющихся в меню?

A) 35

Сколько четырехзначных чисел можно образовать из нечетных цифр, если каждая из этих цифр может повторяться?

D) 625

Группе из пяти сотрудников выделено три путевки. Сколько существует способов распределения путевок, если все путевки различны?

B) 60

Во взводе 3 сержанта и 5 солдат. Сколько существует способов выделения одного сержанта и трех солдат для патрулирования?

E) 30

Сколькими способами можно распределить 10 студентов по двум учебным группам по пять студентов в каждой?

C) 126

Жюри из 5 женщин и 7 мужчин должно быть выбрано из списка в 6 женщин и 10 мужчин. Сколько можно выбрать различных жюри?

B) 720

Сколькими способами, играя в “Спортлото”, можно выбрать 5 номеров из 36 ?

E) 376992

Логическая функция f(x,y,z) задана своими значениями на последовательности наборов значений аргументов (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1):

f = ( 0 1 0 1 0 0 1 1 ). Найдите ее совершенную конъюнктивную нормальную форму (СКНФ).

C) (x V y V z) (x V 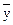V z) ( V y V z)( VyV )

Укажите эквивалентные формулы 1) 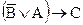2) 3)