
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценивание результатов
Оценка «5» ставится, если студент ответил от 80-100 %;
оценка «4» ставится, если студент ответил от 60-79 %;
оценка «3» ставится, если студент ответил от 40-59 %;
оценка «2» ставится, если студент ответил менее 40 %.
1. Множество натуральных чисел обозначается:
а) Z;
б) N;
в) Q;
г) R.
2. Множество действительных чисел обозначается:
а) Z;
б) N;
в) Q;
г) R.
3. Задайте при помощи характеристического свойства множество, выделенное штриховкой на координатной прямой

-3 0 х
а) [-3;0];
б) [-3;0);
в) (-3;0);
г) (-3;0].
4. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
5. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
6. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
7. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
8. Найдите пересечение множеств А и В, если А={26, 39, 5, 58, 17, 81}, В={17, 26, 58}
а) А 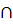 В={17, 26};
В={17, 26};
б) А 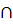 В={17, 26, 58};
В={17, 26, 58};
в) А 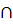 В={17, 26, 5};
В={17, 26, 5};
г) А 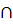 В={58, 26}.
В={58, 26}.
9. Найдите объединение множеств А и В, если А={a, b, c, d, e, f}, В={b, e, f , k}
а) А  В={ a, b, c, d, e, f , k};
В={ a, b, c, d, e, f , k};
б) А  В={ a, b, c, d, e, f };
В={ a, b, c, d, e, f };
в) А  В={ a, b, c, d, e, k};
В={ a, b, c, d, e, k};
г) А  В={ a, b, c, e, f , k}.
В={ a, b, c, e, f , k}.
10. Найдите разность множеств А и В, если А={1, 2, 3, 4, 5, 6}, В={2, 4, 6, 8, 10}
а) А\ В={1, 2, 3, 6};
б) А\ В={1, 2, 3, 8};
в) А\ В={1, 2, 3, 10};
г) А\ В={1, 3, 5}.
11. Перечислить все подмножества множества А, если А={1, 2, 3}:
а) {1, 2, 3}, {1, 2,},{1};
б) {1, 2, 3}, {1, 2,},{1,3},{ 2, 3},{1},{2}, {3}, 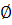 ;
;
в) {1, 2,},{1}, 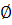 ;
;
г) {1, 2, 3}, {1, 2,}, 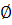 .
.
12. Перечислить элементы множества А, если А – множество нечетных однозначных чисел:
а) 0, 1, 3, 5, 7, 9;
б) 1, 2, 3, 5, 7, 9;
в) 1, 3, 5, 7, 9;
г) 1, 3, 4, 5, 7, 9.
13. Изобразите на координатной плоскости декартово произведение АхВ, если А={1, 2, 3}, В=[3, 5]
а)

б)

в)

г)

14. Выполните действие в двоичной системе счисления 1110101+1101
а) 10000110;
б) 10000010;
в) 10000001;
г) 11000010.
15. Для варки варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара надо взять на 10 кг ягод?
а) 9 кг;
б) 20 кг;
в) 10 кг;
г) 15 кг.
16. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, а другого – 4 км/ч. Через сколько часов они встретились?
а) 4 ч;
б) 2 ч;
в) 3 ч;
г) 5 ч.
17. Ученик затратил на подготовку уроков 1 ч 50 мин. Занятия русским языком заняли на 15 мин больше, чем географией, и на 20 мин меньше, чем математикой. Сколько времени ушло на подготовку каждого предмета отдельно?
а) 25 мин, 40 мин, 45 мин;
б) 30 мин, 30 мин, 50 мин;
в) 35 мин, 20 мин, 55 мин;
г) 15 мин, 60 мин, 35 мин.
18. На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?
а) 1800 км;
б) 1336 км;
в) 1344 км;
г) 1680 км.
19. Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 2 м?
а) 4 кофты;
б) 6 кофт;
в) 3кофты;
г) 5 кофт.
20. Выберите число, которое принадлежит восьмеричной системе счисления:
а) 1234;
б) 1238;
в) 1239;
г) 8888.
21. В шестнадцатеричной системе счисления десятичное число 183 записывается в виде:
а) 117;
б) А7;
в) В7;
г) В8.
22. Запишите число 76108 в виде суммы степеней соответствующего основания с соответствующими коэффициентами:
а) 76108= 7х84+6х83+1х82+0х81;
б) 76108= 7х103+6х102+1х101+0х100;
в) 76108= 0х83+1х82+6х81+7х80;
г) 76108= 7х83+6х82+1х81+0х80 .
23. Как называется вариант из вариационного ряда, имеющий наибольшую частоту:
а) медиана;
б) мода;
в) размах;
г) среднее арифметическое.
24. Как называется значение признака случайной величины, приходящееся на середину ряда:
а) медиана;
б) мода;
в) размах;
г) среднее арифметическое.
25. Как называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней:
а) медиана;
б) мода;
в) размах;
г) выборочная дисперсия.
26. Как называется число, которое является разностью между наибольшим и наименьшим вариантом ряда:
а) медиана;
б) мода;
в) размах;
г) выборочная дисперсия.
27. Как называется совокупность всех подлежащих к изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом:
а) объем;
б) генеральная совокупность;
в) выборка;
г) выборочная совокупность.
28. Как называется совокупность объектов, отобранных случайном образом из генеральной совокупности:
а) объем;
б) генеральная совокупность;
в) реализация выборки;
г) выборочная совокупность.
29. Как называется ряд значений случайной величины, расположенный по неубыванию:
а) группированная выборка;
б) невариационный ряд;
в) статистический ряд;
г) вариационный ряд.
30. Как называется ряд, состоящий из вариантов и соответствующих им частот:
а) группированная выборка;
б) невариационный ряд;
в) статистический ряд;
г) вариационный ряд.
31. В результате тестирования группа набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку статистического ряда:
а)
| хi | ||||||
| yi |
б)
| хi | ||||||
| yi |
в)
| хi | ||||||
| yi |
г)
| хi | ||||||
| yi |
32. В результате тестирования группа набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку в виде вариационного ряда:
а) (0, 1, 2, 3, 4, 5);
б) (1, 1, 2, 3, 4, 4, 5, 5, 5);
в) (0, 1, 1, 2, 3, 4, 4, 5, 5, 5);
г) (0, 1, 1, 2, 3, 4, 4, 5, 5).
33. Графическое представление статистического распределения, где на оси абсцисс откладываются варианты (хi), а на оси ординат – частоты называется:
а) графиком функции распределения;
б) графиком эмпирической функции;
в) полигоном частот;
г) гистограммой частот.
34. Как называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и из трех попарно соединяющих их отрезков:
а) угол;
б) треугольник;
в) луч;
г) пирамида.
35. Каким будет треугольник, если у него две стороны равны:
а) равносторонним;
б) прямоугольным;
в) разносторонним;
г) равнобедренным.
36. Какой четырехугольник обладает свойством, что диагонали взаимно перпендикулярны и точкой пересечения делятся пополам:
а) ромб;
б) прямоугольник;
в) параллелограмм;
г) трапеция.
37. Как называется геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от данной точки:
а) шар;
б) эллипс;
в) окружность;
г) овал.
38. Найти оси эллипса, заданного уравнением 9х2 + 25у2 – 225=0:
а) 5, 6;
б) 10, 6;
в) 10, 3;
г) 5, 3.
39. Составить уравнение окружности с центром S(4; -7) и радиусом r=5:
а) (х-4)2 + (у-7)2 = 25;
б) (х+4)2 + (у+7)2 = 25;
в) (х-4)2 + (у+7)2 = 25;
г) (х-4)2 + (у+7)2 = 5.
40. Как называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников:
а) куб;
б) призма;
в) пирамида;
г) многогранник.
41. Как называется многогранник, у которого одна грань какой-нибудь многоугольник, а остальные грани – треугольники с общей вершиной:
а) куб;
б) призма;
в) пирамида;
г) параллелепипед.
42. Как называется многогранник, у которого две грани какие-либо равные многоугольники, называемые основаниями, и их соответствующие стороны параллельны, а остальные грани – параллелограммы, у каждого из которых две стороны являются сторонами оснований:
а) куб;
б) призма;
в) пирамида;
г) параллелепипед.
43. Прямоугольный параллелепипед, все ребра которого равны, называется:
а) многогранник;
б) призма;
в) пирамида;
г) куб.
44. Множество точек пространства, находящиеся от данной точки на расстоянии, небольшим некоторого данного положительного расстояния называется:
а) окружность;
б) круг;
в) шар;
г) эллипс.
45. Как называется тело, образованное всеми отрезками, соединяющими данную точку, называемую вершиной, с точками некоторого круга:
а) окружность;
б) конус;
в) цилиндр;
г) эллипс.
46. Как называется геометрическое тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей, и перпендикулярных плоскостями оснований:
а) окружность;
б) конус;
в) эллипс;
г) цилиндр.
47. В каком случае существуют на плоскости три точки А, В, С:
а) АС = 15 см, АВ = 8 см, ВС = 7 см;
б) АС = 8 см, АВ = 25 см, ВС = 40 см;
в) АС = 14 см, АВ = 30 см, ВС = 40 см;
г) АС = 14 см, АВ = 3 см, ВС = 4 см.
48. Длину стола измеряли сначала в сантиметрах, потом в дециметрах. В первом случае получили число на 108 больше, чем во втором. Чему равна длина стола?
а) 10 дм;
б) 12 дм;
в) 11 дм;
г) 13 дм.
49. Численное значение длины отрезка, измеренной при помощи единицы Е1 равно 6, а измеренной при помощи единицы Е2 равно 4. В каком отношении находятся между собой единицы длины Е1 и Е2?
а) Е1 больше чем Е2;
б) Е2 больше чем Е1;
в) Е1 и Е2 равны;
г) их нельзя сравнить.
50. Выразить 25 центнеров в тоннах:
а) 0,25 т;
б) 25 т;
в) 2,5 т;
г) 250 т.
51. Выразить ¾ часа в минутах:
а) 20 минут;
б) 30 минут;
в) 45 минут;
г) 15 минут.
52. Укажите натуральное число, предшествующее натуральному числу 1:
а) 0,9;
б) -1;
в) 0;
г) такое число не существует.
53. Как называется разница между точным числом и его приближенным значением:
а) значащими цифрами;
б) погрешность;
в) способ записи приближенного числа;
г) относительная погрешность.
54. Как называется абсолютное значение разности между приближенным числом и его точным значением:
а) значащими цифрами;
б) абсолютная погрешность;
в) способ записи приближенного числа;
г) относительная погрешность.
55. Как называется отношение абсолютной погрешности приближенного числа к самому этому числу:
а) значащими цифрами;
б) абсолютная погрешность;
в) способ записи приближенного числа;
г) относительная погрешность.
56. В результате измерения получены два приближенных числа 2,7 м и 2,62 м, которые требуется сложить. Укажите верные цифры в полученной сумме:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
57. Выполнить сложение и вычитание с наибольшей достижимой точностью, если данные числа даны с точностью до единицы последнего разряда 70,137 + 173,94 — 116,316 — 29,37 + 0,037:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
58. Округлить до четырёх верных значащих цифр числа: 15,7056:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
59. Вычислить приближённое произведение чисел, если первый сомножитель точное число, а второй — приближённое число 254• 3,6:
а) 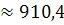 ;
;
б)  ;
;
в)  ;
;
г)  .
.
60. Вычислить частные от деления приближённых чисел 74,1 : 3,8 :
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
61. Где впервые зародилась геометрия:
а) В Древнем Риме;
б) В Древнем Вавилоне;
в) В Древнем Египте;
г) В Индии.
62. Кому принадлежит знаменитый труд «Начала»:
а) Лобачевскому;
б) Фалесу;
в) Пифагору;
г) Евклиду.
63. В каком веке геометрия была построена на аксиоматической основе:
а) не известно;
б) в III веке до н.э.;
в) в II веке до н.э.;
г) в I веке до н.э.
64. В каком веке впервые употребили термин «натуральное число»:
а) не известно;
б) в III веке;
в) в II веке;
г) в V веке.
65. Как называются задачи, сформулированные на естественном языке:
а) нет определения;
б) текстовыми;
в) графическими;
г) утвердительными.
66. Укажите правильную последовательность этапов решения задачи:
а) поиск и составление плана решения задачи; анализ задачи; осуществление плана решения задачи; проверка решения задачи;
б) анализ задачи; осуществление плана решения задачи; поиск и составление плана решения задачи; проверка решения задачи текстовыми;
в) анализ задачи; поиск и составление плана решения задачи; осуществление плана решения задачи; проверка решения задачи;
г) анализ задачи; поиск и составление плана решения задачи; проверка решения задачи; осуществление плана решения задачи.
67. Укажите сколько метров в одном сажени:
а) 1,36;
б) 2,422;
в) 2,134;
г) 21,34.
Дата добавления: 2015-01-05; просмотров: 455; Мы поможем в написании вашей работы!; Нарушение авторских прав |