
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы дистанционного зондирования Земли. Оценка «5» ставится, если студент ответил от 80-100 %;
Оценка «5» ставится, если студент ответил от 80-100 %;
оценка «4» ставится, если студент ответил от 60-79 %;
оценка «3» ставится, если студент ответил от 40-59 %;
оценка «2» ставится, если студент ответил менее 40 %.
1. Множество натуральных чисел обозначается:
а) Z;
б) N;
в) Q;
г) R.
2. Множество действительных чисел обозначается:
а) Z;
б) N;
в) Q;
г) R.
3. Задайте при помощи характеристического свойства множество, выделенное штриховкой на координатной прямой

-3 0 х
а) [-3;0];
б) [-3;0);
в) (-3;0);
г) (-3;0].
4. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
5. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
6. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
7. При помощи кругов Эйлера для множеств А и В изображено

а) пересечение множеств А и В;
б) объединение множеств А и В;
в) дополнение множества В до множества А;
г) вычитание из множества А множество В.
8. Найдите пересечение множеств А и В, если А={26, 39, 5, 58, 17, 81}, В={17, 26, 58}
а) А 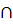 В={17, 26};
В={17, 26};
б) А 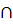 В={17, 26, 58};
В={17, 26, 58};
в) А 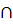 В={17, 26, 5};
В={17, 26, 5};
г) А 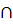 В={58, 26}.
В={58, 26}.
9. Найдите объединение множеств А и В, если А={a, b, c, d, e, f}, В={b, e, f , k}
а) А  В={ a, b, c, d, e, f , k};
В={ a, b, c, d, e, f , k};
б) А  В={ a, b, c, d, e, f };
В={ a, b, c, d, e, f };
в) А  В={ a, b, c, d, e, k};
В={ a, b, c, d, e, k};
г) А  В={ a, b, c, e, f , k}.
В={ a, b, c, e, f , k}.
10. Найдите разность множеств А и В, если А={1, 2, 3, 4, 5, 6}, В={2, 4, 6, 8, 10}
а) А\ В={1, 2, 3, 6};
б) А\ В={1, 2, 3, 8};
в) А\ В={1, 2, 3, 10};
г) А\ В={1, 3, 5}.
11. Перечислить все подмножества множества А, если А={1, 2, 3}:
а) {1, 2, 3}, {1, 2,},{1};
б) {1, 2, 3}, {1, 2,},{1,3},{ 2, 3},{1},{2}, {3}, 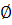 ;
;
в) {1, 2,},{1}, 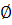 ;
;
г) {1, 2, 3}, {1, 2,}, 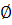 .
.
12. Перечислить элементы множества А, если А – множество нечетных однозначных чисел:
а) 0, 1, 3, 5, 7, 9;
б) 1, 2, 3, 5, 7, 9;
в) 1, 3, 5, 7, 9;
г) 1, 3, 4, 5, 7, 9.
13. Изобразите на координатной плоскости декартово произведение АхВ, если А={1, 2, 3}, В=[3, 5]
а)

б)

в)

г)

14. Выполните действие в двоичной системе счисления 1110101+1101
а) 10000110;
б) 10000010;
в) 10000001;
г) 11000010.
15. Для варки варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара надо взять на 10 кг ягод?
а) 9 кг;
б) 20 кг;
в) 10 кг;
г) 15 кг.
16. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, а другого – 4 км/ч. Через сколько часов они встретились?
а) 4 ч;
б) 2 ч;
в) 3 ч;
г) 5 ч.
17. Ученик затратил на подготовку уроков 1 ч 50 мин. Занятия русским языком заняли на 15 мин больше, чем географией, и на 20 мин меньше, чем математикой. Сколько времени ушло на подготовку каждого предмета отдельно?
а) 25 мин, 40 мин, 45 мин;
б) 30 мин, 30 мин, 50 мин;
в) 35 мин, 20 мин, 55 мин;
г) 15 мин, 60 мин, 35 мин.
18. На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?
а) 1800 км;
б) 1336 км;
в) 1344 км;
г) 1680 км.
19. Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 2 м?
а) 4 кофты;
б) 6 кофт;
в) 3кофты;
г) 5 кофт.
20. Выберите число, которое принадлежит восьмеричной системе счисления:
а) 1234;
б) 1238;
в) 1239;
г) 8888.
21. В шестнадцатеричной системе счисления десятичное число 183 записывается в виде:
а) 117;
б) А7;
в) В7;
г) В8.
22. Запишите число 76108 в виде суммы степеней соответствующего основания с соответствующими коэффициентами:
а) 76108= 7х84+6х83+1х82+0х81;
б) 76108= 7х103+6х102+1х101+0х100;
в) 76108= 0х83+1х82+6х81+7х80;
г) 76108= 7х83+6х82+1х81+0х80 .
23. Как называется вариант из вариационного ряда, имеющий наибольшую частоту:
а) медиана;
б) мода;
в) размах;
г) среднее арифметическое.
24. Как называется значение признака случайной величины, приходящееся на середину ряда:
а) медиана;
б) мода;
в) размах;
г) среднее арифметическое.
25. Как называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней:
а) медиана;
б) мода;
в) размах;
г) выборочная дисперсия.
26. Как называется число, которое является разностью между наибольшим и наименьшим вариантом ряда:
а) медиана;
б) мода;
в) размах;
г) выборочная дисперсия.
27. Как называется совокупность всех подлежащих к изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом:
а) объем;
б) генеральная совокупность;
в) выборка;
г) выборочная совокупность.
28. Как называется совокупность объектов, отобранных случайном образом из генеральной совокупности:
а) объем;
б) генеральная совокупность;
в) реализация выборки;
г) выборочная совокупность.
29. Как называется ряд значений случайной величины, расположенный по неубыванию:
а) группированная выборка;
б) невариационный ряд;
в) статистический ряд;
г) вариационный ряд.
30. Как называется ряд, состоящий из вариантов и соответствующих им частот:
а) группированная выборка;
б) невариационный ряд;
в) статистический ряд;
г) вариационный ряд.
31. В результате тестирования группа набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку статистического ряда:
а)
| хi | ||||||
| yi |
б)
| хi | ||||||
| yi |
в)
| хi | ||||||
| yi |
г)
| хi | ||||||
| yi |
32. В результате тестирования группа набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку в виде вариационного ряда:
а) (0, 1, 2, 3, 4, 5);
б) (1, 1, 2, 3, 4, 4, 5, 5, 5);
в) (0, 1, 1, 2, 3, 4, 4, 5, 5, 5);
г) (0, 1, 1, 2, 3, 4, 4, 5, 5).
33. Графическое представление статистического распределения, где на оси абсцисс откладываются варианты (хi), а на оси ординат – частоты называется:
а) графиком функции распределения;
б) графиком эмпирической функции;
в) полигоном частот;
г) гистограммой частот.
34. Как называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и из трех попарно соединяющих их отрезков:
а) угол;
б) треугольник;
в) луч;
г) пирамида.
35. Каким будет треугольник, если у него две стороны равны:
а) равносторонним;
б) прямоугольным;
в) разносторонним;
г) равнобедренным.
36. Какой четырехугольник обладает свойством, что диагонали взаимно перпендикулярны и точкой пересечения делятся пополам:
а) ромб;
б) прямоугольник;
в) параллелограмм;
г) трапеция.
37. Как называется геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от данной точки:
а) шар;
б) эллипс;
в) окружность;
г) овал.
38. Найти оси эллипса, заданного уравнением 9х2 + 25у2 – 225=0:
а) 5, 6;
б) 10, 6;
в) 10, 3;
г) 5, 3.
39. Составить уравнение окружности с центром S(4; -7) и радиусом r=5:
а) (х-4)2 + (у-7)2 = 25;
б) (х+4)2 + (у+7)2 = 25;
в) (х-4)2 + (у+7)2 = 25;
г) (х-4)2 + (у+7)2 = 5.
40. Как называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников:
а) куб;
б) призма;
в) пирамида;
г) многогранник.
41. Как называется многогранник, у которого одна грань какой-нибудь многоугольник, а остальные грани – треугольники с общей вершиной:
а) куб;
б) призма;
в) пирамида;
г) параллелепипед.
42. Как называется многогранник, у которого две грани какие-либо равные многоугольники, называемые основаниями, и их соответствующие стороны параллельны, а остальные грани – параллелограммы, у каждого из которых две стороны являются сторонами оснований:
а) куб;
б) призма;
в) пирамида;
г) параллелепипед.
43. Прямоугольный параллелепипед, все ребра которого равны, называется:
а) многогранник;
б) призма;
в) пирамида;
г) куб.
44. Множество точек пространства, находящиеся от данной точки на расстоянии, небольшим некоторого данного положительного расстояния называется:
а) окружность;
б) круг;
в) шар;
г) эллипс.
45. Как называется тело, образованное всеми отрезками, соединяющими данную точку, называемую вершиной, с точками некоторого круга:
а) окружность;
б) конус;
в) цилиндр;
г) эллипс.
46. Как называется геометрическое тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей, и перпендикулярных плоскостями оснований:
а) окружность;
б) конус;
в) эллипс;
г) цилиндр.
47. В каком случае существуют на плоскости три точки А, В, С:
а) АС = 15 см, АВ = 8 см, ВС = 7 см;
б) АС = 8 см, АВ = 25 см, ВС = 40 см;
в) АС = 14 см, АВ = 30 см, ВС = 40 см;
г) АС = 14 см, АВ = 3 см, ВС = 4 см.
48. Длину стола измеряли сначала в сантиметрах, потом в дециметрах. В первом случае получили число на 108 больше, чем во втором. Чему равна длина стола?
а) 10 дм;
б) 12 дм;
в) 11 дм;
г) 13 дм.
49. Численное значение длины отрезка, измеренной при помощи единицы Е1 равно 6, а измеренной при помощи единицы Е2 равно 4. В каком отношении находятся между собой единицы длины Е1 и Е2?
а) Е1 больше чем Е2;
б) Е2 больше чем Е1;
в) Е1 и Е2 равны;
г) их нельзя сравнить.
50. Выразить 25 центнеров в тоннах:
а) 0,25 т;
б) 25 т;
в) 2,5 т;
г) 250 т.
51. Выразить ¾ часа в минутах:
а) 20 минут;
б) 30 минут;
в) 45 минут;
г) 15 минут.
52. Укажите натуральное число, предшествующее натуральному числу 1:
а) 0,9;
б) -1;
в) 0;
г) такое число не существует.
53. Как называется разница между точным числом и его приближенным значением:
а) значащими цифрами;
б) погрешность;
в) способ записи приближенного числа;
г) относительная погрешность.
54. Как называется абсолютное значение разности между приближенным числом и его точным значением:
а) значащими цифрами;
б) абсолютная погрешность;
в) способ записи приближенного числа;
г) относительная погрешность.
55. Как называется отношение абсолютной погрешности приближенного числа к самому этому числу:
а) значащими цифрами;
б) абсолютная погрешность;
в) способ записи приближенного числа;
г) относительная погрешность.
56. В результате измерения получены два приближенных числа 2,7 м и 2,62 м, которые требуется сложить. Укажите верные цифры в полученной сумме:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
57. Выполнить сложение и вычитание с наибольшей достижимой точностью, если данные числа даны с точностью до единицы последнего разряда 70,137 + 173,94 — 116,316 — 29,37 + 0,037:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
58. Округлить до четырёх верных значащих цифр числа: 15,7056:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
59. Вычислить приближённое произведение чисел, если первый сомножитель точное число, а второй — приближённое число 254• 3,6:
а) 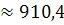 ;
;
б)  ;
;
в)  ;
;
г)  .
.
60. Вычислить частные от деления приближённых чисел 74,1 : 3,8 :
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
61. Где впервые зародилась геометрия:
а) В Древнем Риме;
б) В Древнем Вавилоне;
в) В Древнем Египте;
г) В Индии.
62. Кому принадлежит знаменитый труд «Начала»:
а) Лобачевскому;
б) Фалесу;
в) Пифагору;
г) Евклиду.
63. В каком веке геометрия была построена на аксиоматической основе:
а) не известно;
б) в III веке до н.э.;
в) в II веке до н.э.;
г) в I веке до н.э.
64. В каком веке впервые употребили термин «натуральное число»:
а) не известно;
б) в III веке;
в) в II веке;
г) в V веке.
65. Как называются задачи, сформулированные на естественном языке:
а) нет определения;
б) текстовыми;
в) графическими;
г) утвердительными.
66. Укажите правильную последовательность этапов решения задачи:
а) поиск и составление плана решения задачи; анализ задачи; осуществление плана решения задачи; проверка решения задачи;
б) анализ задачи; осуществление плана решения задачи; поиск и составление плана решения задачи; проверка решения задачи текстовыми;
в) анализ задачи; поиск и составление плана решения задачи; осуществление плана решения задачи; проверка решения задачи;
г) анализ задачи; поиск и составление плана решения задачи; проверка решения задачи; осуществление плана решения задачи.
67. Укажите сколько метров в одном сажени:
а) 1,36;
б) 2,422;
в) 2,134;
г) 21,34.
Методы дистанционного зондирования Земли
Фотографический метод. Оптико-электронный метод. Радиолокационный метод.
Дистанционные методы делят на активные и пассивные. При использовании активных методов спутник посылает на Землю сигнал собственного источника энергии (лазера, радиолокационного передатчика), регистрирует его отражение. Радиолокация позволяет «видеть» Землю сквозь облака. Чаще используются пассивные методы, когда регистрируется отраженная поверхностью энергия Солнца либо тепловое излучение Земли.
По применяемой аппаратуре их подразделяют на: фотографические, телевизионные, инфракрасные или тепловизионные, радиолокационные, лазерные, сканирующие, оптико-электронные и другие.
Фотографические съемочные системы. Первые изображения Земли из космоса были получены с помощью фотокамеры, которая формирует перекрывающие кадры изображений местности на фотопленке.

Рис. Кадровые снимки: горизонтальная штриховка – двойное перекрытие; наклонная – тройное перекрытие снимков.
Отснятые материалы спускаются на Землю и проявляются. Анализ снимков, как правило, проводится визуально с помощью проекционной аппаратуры, которая позволяет также получать цветные фотоотпечатки. Метод обеспечивает высокую геометрическую точность изображения, использование отработанных способов и технических средств фотограмметрической обработки материалов. Недостатки: мало оперативен, в связи с необходимостью доставки снимков на Землю, кроме того изображение представлено в виде фотографий, а не в цифровой форме.
Телевизионная съемка. По принципу работы кадровая телевизионная съемка напоминают фотографические, только вместо фотопленки в фокальной плоскости объектива устанавливается миниатюрная телевизионная камера. Оптическое изображение, построенное объективом на телевизионном мониторе, при считывании электронным лучом переводится в форму электрических сигналов и по радиоканалу передается на наземный приемный пункт и воспроизводится уже на мониторе оператора.
 |
Сканерная съемка. При сканерной съемке сканирующие системы используют качающееся зеркало на борту носителя, которое улавливает отраженный от Земли световой сигнал и создает строку изображения. Преобразованные сигналы сканера по радиоканалам передаются на Землю, где на приемных станциях принимаются и восстанавливают изображение. При сканировании каждый сигнал (пиксель) передает обобщенные характеристики элемента земной поверхности. Совокупность строк, формирующийся при поступательном движении носителя, формирует снимок. Сканерная информация в цифровой форме передается со спутника в режиме реального времени или в записи на бортовой магнитофон, на Земле она обрабатывается на ЭВМ.
Рисунок 2. Схема сканирования поверхности Земли
Сканерная съемка уступает фотографической съемке по качеству снимков, разрешение снимков достигает 30 м.
Радиолокационная съемка.Принцип активной радиолокации состоит в облучении объекта наблюдения активной станцией (радаром), фиксации отражения этого излучения и получении радиолокационных снимков Интенсивность отраженных сигналов зависит от дальности и различна для различных объектов, так как они отличаются размерами и электрофизическими характеристиками. Для радарной съемки используется
сантиметровый диапазон радиоволн. Важнейшее преимущество снимков этого класса – в их всепогодности. Поскольку радар регистрирует собственное, отраженное земной поверхностью, излучение, для его работы не требуется солнечный свет. Кроме того, радиоволны этого диапазона свободно проходят через сплошную облачность и даже способны проникать на некоторую глубину в почву. Это называют подповерхностным зондированием, диапазон работы дециметровый и метровый (1-30 м). Так, например, подповерхностное зондирование в диапазоне 0,5-1 м позволяет выявлять пресные грунтовые воды в песках на глубине до 20 м, радары также способны фиксировать наличие нефтяной пленки толщиной 50 мкм. Радиолокатор, перемещаясь вместе со спутником, последовательно считывает по строкам сигнал с различной интенсивностью, пропорциональной отражательной способностью различных участков поверхности. Строки, как и в сканерах оптического диапазона, расположены поперек движения спутника.

Рисунок 3. Схема работы радиолокатора бокового обзора
Тепловые съемки. Тепловая или инфракрасная съемка (ИК)), основана на выявлении тепловых аномалий путем фиксации теплового излучения объектов Земли, обусловленного эндогенным теплом или солнечным излучением. Эта съемка широко применяется в геологии. Температурные неоднородности поверхности Земли возникают в результате неодинакового нагрева различных ее участков. Полученных с ИСЗ инфракрасных снимках, четко вырисовывается береговая линия, гидрографическая сеть, ледовая обстановка, тепловые неоднородности водной среды, вулканическая деятельность и т.п. инфракрасные снимки используются для составления тепловых карт Земли. Линейно-полосовые тепловые аномалии, выявляемые при инфракрасной съемке, интерпретируются как зоны разломов, а площадные и концентрические — как тектонические или орографические структуры. Спектрометрическая съемка проводится с целью измерения отражательной способности горных пород.
Контрольные задания
1. Методы ДЗЗ.
2. Фотографические системы
3. Сканирование оптико-электронных систем.
4. Радиолокационные съемочные системы.
Используемая литература
1. Пудовкин О.Л.
2 Назаров А.С. Фотограмметрия: учебное пособие для вузов. Мн.: ТетраСистемс, 2006- 368 с.
3.Геодезия, картография, геоинформатика, кадастр. Энциклопедия. Под общей редакцией А.В. Бородко, В.П. Савиных М., Геодезкартиздат, 2008
4. Лабутина И.А. Дешифрирование аэрокосмических снимков. Учебное пособие. Изд. Аспект Пресс, 2004
Дата добавления: 2015-01-05; просмотров: 695; Мы поможем в написании вашей работы!; Нарушение авторских прав |