
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тип Баланса #3: Осмысленный выбор
Есть много разных способов поставить игрока перед выбором. Если он стоит перед осмысленным выбором, он спросит себя:
● Куда я должен идти?
● Как я должен тратить свои ресурсы?
● Какие умения мне нужно отточить до совершенства?
● Как мне одеть моего персонажа?
● Игру лучше проходить быстро или осторожно?
● Мне лучше сосредоточиться на атаке или на защите?
● Какую стратегию использовать в этой ситуации?
● Какую силу мне лучше выбрать?
● Нужно или не нужно рисковать?
Хорошие игры ставят игрока перед осмысленным выбором. Не просто перед выбором, а перед выбором, который повлияет на последующие события в игре и на то, как игра будет продолжаться. Многие дизайнеры загоняют себя в ловушку, ставя игрока перед бессмысленным выбором; например, в гоночных симуляторах вы можете выбрать себе одну из 50-ти машин, но если их показатели равны, получается, что выбора у вас нет. Другие дизайнеры загоняют себя в еще одну ловушку – предлагая игрокам выбирать то, что никто выбрать не захочет. Вы можете предложить игрокам 10 различных пистолетов, но если один из них имеет очевидное преимущество над остальными, то, опять же, выбора у игроков нет.
Когда игроку предоставляется выбор, но один из вариантов выбора очевидно лучше всех остальных, это называется доминирующей стратегией (dominant strategy). Как только игрок обнаруживает доминирующую стратегию, игра теряет основную долю фана, потому, что загадка игры в этот момент считается решенной – больше не остается никаких выборов. Когда вы обнаружите, что в игре, над которой вы работаете, есть доминирующая стратегия, вы должны изменить правила (сбалансировать все) таким образом, чтобы эта стратегия перестала доминировать, а в геймплее появились осмысленные варианты выбора. Предыдущий пример с “Битвой Бипланов” можно привязать и к этому правилу – дизайнер пытается сбалансировать игру, чтобы убрать доминирующую стратегию и вернуть игроку возможность сделать осмысленный выбор. Скрытые доминирующие стратегии, которые игроки обнаруживают сами, часто относят к понятию “эксплуатации”, поскольку игроки могут эксплуатировать их для того, чтобы “протоптать” короткий путь к успеху, о существовании которого дизайнер и не подозревал.
На ранних этапах разработки игры доминирующие стратегии присутствуют в большом количестве. Но с каждым последующим этапом балансировка игры приводит к сокращению их количества. Как это ни парадоксально, но начинающих дизайнеров это приводит в панику: “Вчера я понял, как нужно играть в эту игру – но после всех этих новых изменений, я уже и не знаю, правильно ли я играю!” Они считают, что потеряли контроль над своей собственной игрой. Но на самом деле, игра просто сделала большой шаг вперед! В ней больше нет доминирующей стратегии, и теперь пришло время делать осмысленный выбор. Вместо того чтобы бояться этой ситуации, вы должны радоваться ей, воспользоваться возможностью и понять, каким образом текущая конфигурация правил и значений сбалансировала вашу игру.
Но это приводит нас к другому вопросу: Сколько осмысленных выборов мы должны предоставить игроку? Майкл Матис (Michael Mateas) указывает на то, что количество вариантов выбора, необходимых игроку, зависит от количества вещей, которые он желает.
● Если Вариантов Выбора > Желаний, игрок слишком переполнен
● Если Вариантов Выбора < Желаний, игрок расстраивается
● Если Варианты Выбора = Желаниям, игрок получает ощущение свободы и удовлетворенности
Значит, чтобы правильно определить количество вариантов выбора, вам нужно рассчитать типы и количество вещей, которые игроки захотят делать. В некоторых ситуациях игроку нужно небольшое количество осмысленных вариантов выбора (выбирать между левым и правым поворотом на развилке будет интересно, но выбирать между 30 различными поворотами – это слишком). В другом случае, желательно большое количество вариантов выбора (например, интерфейс магазина одежды в The Sims).
Осмысленные варианты выбора – это основа интерактивности, поэтому следующую линзу будет полезен всем без исключения.
| Линза #32: Линза Осмысленного Выбора |
| Когда мы делаем осмысленный выбор, это позволяет нам ощутить значимость наших действий. Чтобы воспользоваться этой линзой, спросите себя: ● Перед каким выбором я ставлю игрока? ● Это осмысленный выбор? Почему? ● Я предоставляю игроку правильное количество вариантов выбора? Может ли большее количество вариантов выбора заставить игрока почувствовать больше власти? Если уменьшить их количество, станет ли игра более понятной? ● В моей игре есть доминирующие стратегии? |
Треугольность
Один из самых интересных выборов, который игрок может сделать – играть без риска и получить небольшую награду или серьезно рискнуть, в надежде сорвать куш. Подобные решения всегда даются очень трудно, если игра правильно сбалансирована. Я обнаружил, что в восьми из десяти случаев, когда ко мне приходят за помощью с прототипом игры, в которой “нет фана”, проблема заключается в отсутствии осмысленного выбора. Это иногда называют “риском асимметричного баланса”, поскольку вы балансируете небольшие риски с небольшим вознаграждением вместе с большими рисками с большим вознаграждением, но такое название сложно произносить. Эти отношения возникают настолько часто, и они настолько важны, что я придумал более удобное название: треугольность. Игрок – это один угол треугольника, выбор с небольшим риском – второй, а выбор с большим риском – третий.
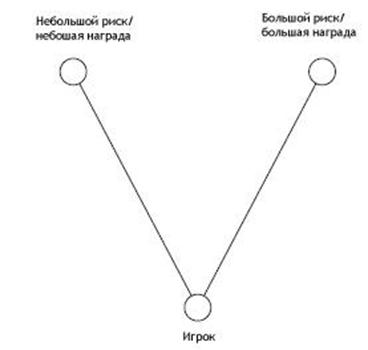
Рис. 11.2
Пример игры с правильно реализованной треугольностью – Space Invaders. Большую часть времени вы стреляете снизу по пришельцам возле вашего корабля, которые стоят 10, 20 и 30 очков. Они медлительны, поэтому в них легко попасть, а сбивая их, вы увеличиваете вероятность избежать падающих бомб, которые сбрасывают пришельцы. Однако периодически вверху экрана пролетает маленькая летающая тарелка красного цвета. Сама по себе она не несет угрозы, но попасть в нее трудно и опасно. Трудно потому, что тарелка летает очень далеко, а опасно потому, что для того, чтобы хорошо прицелиться, вам нужно переключить внимание со своего корабля на нее, что увеличивает риск попадания в вас бомбы. Но если вы попадете, то получите от 100 до 300 очков! Без летающей тарелки Space Invaders были бы слишком скучными, потому что вам было бы не из чего выбирать – вы бы просто стреляли, стреляли и стреляли. Но с летающей тарелкой перед вами вдруг появляется сложный, осмысленный выбор – сыграть осторожно, или рискнуть ради большего количества очков? Треугольность настолько важна, что вам не обойтись без следующей линзы.
| Линза #33: Линза Треугольности |
| Предоставляя игроку выбор — сыграть осторожно и получить меньшую награду, или рискнуть, чтобы больше, вы делаете свою игру захватывающей и интересной. Чтобы воспользоваться Линзой Треугольности, спросите себя: ● В моей игре присутствует треугольность? Если нет, как мне это исправить? ● Треугольность моей игры достаточно сбалансирована? Иными словами, соответствует ли награда риску? Как только вы начнете искать треугольность в играх, вы будете находить ее повсюду. Даже самая скучная и монотонная игра может быстро стать захватывающей, если вы добавите в нее немного треугольности. |
Отличный способ убедиться в том, что треугольность вашей игры правильно сбалансирована – использовать Линза #28: Линза Ожидаемого Значения. В классической игре Qix можно найти интересный пример балансировки с использованием ожидаемого значения. В этой игре вы рисуете прямоугольные формы с целью окружить территорию на пустом игровом поле. Пока вы это делаете, совокупность линий, которые называются квиксы, в случайном порядке передвигаются по полю. Если квикс касается вашего прямоугольника до того, как вы закончите его рисовать, вы умираете. Но если вы успеете закончить прямоугольник, вы захватите территорию, равную его размеру. Захватив 75% игрового поля, вы побеждаете на уровне.
Дизайнеры предоставили игроку вполне понятный выбор: каждый раз, когда он рисует прямоугольник, он может сделать это быстро (рисуя синий прямоугольник) или медленно (рисуя оранжевый прямоугольник). Поскольку, двигаясь в два раза медленнее, игрок подвергается в два раза большей опасности, прямоугольники, нарисованные с меньшей скоростью, приносят в два раза больше очков. Это работает, потому что если учесть, что шанс успешно нарисовать быстрый, синий прямоугольник составляет 20%, а его стоимость – 100 очков, ожидаемое значение нарисовать оный – 100 очков х 20% = 20 очков. Мы также знаем, что рисование прямоугольника на второй скорости, которая в два раза ниже первой, имеет в два раза меньший шанс на успех, поэтому мы получаем следующую таблицу:
| Скорость | Вероятность успеха | Очки | Ожидаемое значение |
| Быстрый (синий) | 20% | ||
| Медленный (оранжевый) | 10% | ? |
Если мы хотим, чтобы игра была сбалансированной, нам нужно сохранять постоянное ожидаемое значение. Очень легко увидеть, что если мы хотим, чтобы игра была сбалансирована, ценность медленного прямоугольника одинакового размера должна составлять 200 очков. Самая тяжелая часть – высчитать шансы на успех – нам часто приходится считать – но это уже другой случай, где модель информирует прототип, а тестирование прототипа информирует модель, создавая “круг благоразумия”, где результат одного события усиливает эффект другого, модель правильная, а игра сбалансирована.
Дата добавления: 2015-01-05; просмотров: 233; Мы поможем в написании вашей работы!; Нарушение авторских прав |