
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Андай матрицаның кері матрицасы болады?
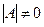 болса
болса
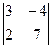 анықтауышын есепте
анықтауышын есепте
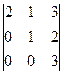 анықтауышын есепте
анықтауышын есепте
 матрицасының рангысының анықтамасы: осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады
матрицасының рангысының анықтамасы: осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады
Матрицаның рангысы өзгермейді, егер:
кез келген екі жолын немесе екі бағанын ауыстырғаннан
Егер бір матрица екінші бір матрицадан элементар (жәй) түрлендіру арқылы алынса, онда ол матрицалар:
эквивалентті деп аталады.
 анықтауышын есепте
анықтауышын есепте
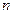 белгісізді
белгісізді 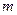 сызықты алгебралық теңдеулер жүйесі үйлесімді, егер:
сызықты алгебралық теңдеулер жүйесі үйлесімді, егер:
жүйенің негізгі матрицасының рангысы мен оның кеңейтілген матрицасының рангысына тең болса
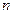 белгісізді
белгісізді 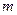 сызықты алгебралық теңдеулер жүйесінің бір ғана шешімі болады, егер:
сызықты алгебралық теңдеулер жүйесінің бір ғана шешімі болады, егер:
жүйенің негізгі матрицасының рангысы оның кеңейтілген матрицасының рангысына тең және ол белгісіздер саны  -ге тең, яғни
-ге тең, яғни 
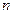 белгісізді
белгісізді 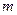 біртекті сызықты алгебралық теңдеулер жүйесі:
біртекті сызықты алгебралық теңдеулер жүйесі:
әруақытта үйлесімді
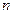 белгісізі бар
белгісізі бар 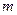 сызықты теңдеулер жүйесі
сызықты теңдеулер жүйесі 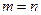 болғанда, мұнда
болғанда, мұнда 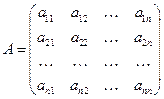
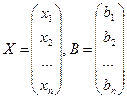 , матрицалық түрде былай беріледі.
, матрицалық түрде былай беріледі.
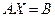
 белгісізді
белгісізді  сызықты теңдеулер жүйесінің матрицалық әдіспен шешкендегі матрица - шешімі
сызықты теңдеулер жүйесінің матрицалық әдіспен шешкендегі матрица - шешімі 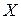 былай табылады:
былай табылады:
A) 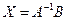
 белгісізді
белгісізді  сызықты алгебралық теңдеулер жүйесінің
сызықты алгебралық теңдеулер жүйесінің 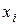 шешімі
шешімі 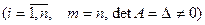 Крамер формуласы бойынша былай табылады:
Крамер формуласы бойынша былай табылады:
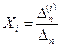
Біртекті 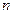 белгісізді
белгісізді 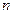 сызықты теңдеулер жүйесінің бір ғана шешімі бар:
сызықты теңдеулер жүйесінің бір ғана шешімі бар:
 , егер
, егер 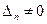
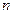 белгісізді
белгісізді 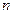 біртекті теңдеулер жүйесінің шексіз көп шешімі болады, егер:
біртекті теңдеулер жүйесінің шексіз көп шешімі болады, егер:
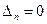
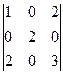 анықтауышын есептеңіз:
анықтауышын есептеңіз:
-2
 анықтауышын есептеңіз:
анықтауышын есептеңіз:
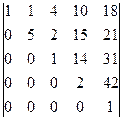 анықтауышын есептеңіз:
анықтауышын есептеңіз:
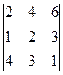 анықтауышын есептеңіз:
анықтауышын есептеңіз:
 анықтауышын есептеңіз:
анықтауышын есептеңіз:
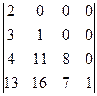 анықтауышын есептеңіз:
анықтауышын есептеңіз:
 анықтауышының
анықтауышының 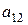 элементінің минорын есептеңіз:
элементінің минорын есептеңіз:
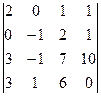 анықтауышының
анықтауышының 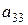 элементінің минорын есептеңіз:
элементінің минорын есептеңіз:
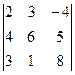 анықтауышының
анықтауышының  элементінің минорын есептеңіз:
элементінің минорын есептеңіз:
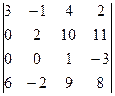 анықтауышының
анықтауышының  элементінің минорын есептеңіз:
элементінің минорын есептеңіз:
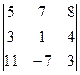 анықтауышының
анықтауышының 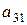 элементінің
элементінің 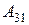 алгебралық толықтауышын есептеңіз:
алгебралық толықтауышын есептеңіз:
Дата добавления: 2015-01-05; просмотров: 370; Мы поможем в написании вашей работы!; Нарушение авторских прав |