Түріндегі өрнек шексіз...деп аталады 1 страница

Волков В.К, Цикулин Л.Е. Лечение и реабилитация больных гипертонической болезнью в условиях поликлиники. – М., 1989.

Героева И.Б., Назаров Г.Ф., Епифанов В.А. Лечебная гимнастика в терапии остеохондроза позвоночника. – М.: Медицина, 1975.

Демиденко Т.Д. Реабилитация при цереброваскулярной патологии. – Л., 1989.

Епифанов В.А., Ролик И. С. Средства физической реабилитации в терапии остеохондроза позвоночника. – М., 1997.

Каптелин А Ф. ЛФК и средства реабилитации больных с повреждением спинного мозга. – М., 1968.

Кочеткова И.Н. Парадоксальная гимнастика Стрельниковой. – М., 1989.

Ковалев Н.А. Поясничный остеохондроз. – М., 1996.

Коган О.Г. Реабилитация больных при травмах позвоночника и спинного мозга. – М., 1975.

Лечебная физическая культура: Справочник / Под ред. проф. В.А. Епифанова. – М., 2002.

Лечебная физическая культура: Справочник / Под ред. проф. И.М. Саркизова-Серазини. - М., 1954.

Лечебная физкультура в реабилитации постинсультных больных / В.К. Добровольский, А.М. Вишневская, В.А. Коровицинаи др. – Л., 1986.

Ловейко И.Д., Фонарев М.И. Лечебная физкультура при заболеваниях позвоночника у детей. – 2-е изд., перераб. – Л., 1988.

Медицинская реабилитация. Т. I–III / Под ред. акад. РАМН, проф. В.М. Богомолова. – М.; Пермь, 1998.

Найдин В.Л. Реабилитация нейрохирургических больных с двигательными нарушениями. – М., 1972.

Николаева Л.Ф., Аронов Д.М. Реабилитация больных с ишемической болезнью сердца. - М., 1988.

Оганов Р.Г. Профилактика сердечно-сосудистых заболеваний: возможности практического здравоохранения // Кардиоваскулярная терапия и профилактика. – 2002. – № 1. – С. 5.

Пропастин Г.Н. Клинико-физиологическое обоснование применения лечебной физкультуры при заболеваниях желудка: Автореф. дис. ... д-ра мед. наук. – М., 1970.

Реабилитация больных после аортокоронарного шунтирования: Методические рекомендации / Сост. Г.В. Громова и др. – М., 1991.

Реабилитация больных с некоторыми заболеваниями и повреждениями кисти: Сб. науч. тр. Горьк. НИИ травматологии и ортопедии / Под ред. В.В.Азолова. – Горький, 1987.

Судаков КВ. Общая теория функциональных систем. – М., 1984.

Тёмкин И.Б. Лечебная физкультура при первичной артериальной гипертонии. – М., 1971.

Транквиллитати А.Н. Организация занятий ЛФК для больных с поражением спинного мозга в лечебно-профилактических учреждениях: Методические рекомендации. – М., 1982.

Фонарев М.И., Фонарева Т.А. Лечебная физкультура при детских заболеваниях. – Л., 1981.

Шарафанов А.А. Лечебная гимнастика при заболеваниях органов пищеварения, мочеполовой системы и ожирении. – Ставрополь, 1988.

Шорин Г.А., Попова Т.Н., Полякова P.M. Консервативное лечение сколиоза: Учеб. пособие. – Челябинск, 2000.

Юденич В.В., Гришкович В.М. Руководство по реабилитации обожженных. - М., 1986.

Юмашев Г.С. Травматология и ортопедия. – М., 1977.

түріндегі өрнек шексіз...деп аталады

$$сандық қатар

$тізбек

$шегі

$функционал

$$$24 қатарының дербес қосындылар тізбегінің ақырлы .... бар болса, онда берілген тізбек жинақты деп аталады.

$$шегі

$реті

$саны

$функциясы

$$$25 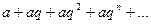геометриялық прогрессия қатары еселігі болғанда жинақты болады.

$$бірден кіші

$бір

$екі

$үш

$$$26 шегі бар болса, онда қатары ... деп аталады.

$$жинақты

$жинақсыз

$шартты жинақты

$абсолют жинақты

$$$27 Егер сан қатары жинақты болса, онда оның жалпы мүшесінің шегі....ұмтылады.

$$нөлге

$бірге

$үшке

$екіге

$$$28 Егер сан қатары жинақты болса, онда оның дербес қосындыларының тізбегі....санға ұмтылады.

$$шектелген

$шектелмеген

$бірге

$үшке

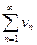$$$29 Егер және -оң сандар қатары мүшелерінекез келген үшін теңсіздігі орындалса, онда 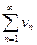қатарының жинақтылығынан қатарының....болуы шығады.

$$жинақты

$жинақсыз

$шартты жинақты

$абсолют жинақты

$$$30 Егер екі оң сандар қатарының жалпы мүшелері үшін мұндағы нолге тең емес кез келген сан, теңдігі орындалса, онда екеуіде....не жинақты, не жинақсыз болады

$$бірдей

$әртүрлі

$шартты

$абсолют

$$$31 Егер 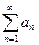оң сандар қатары үшін , шарты орындалса, онда берілген қатар....

$$жинақсыз

$жинақты

$абсолют жинақты

$шартты жинақты

$$$32 Егер 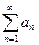- оң сандар қатары үшін 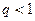, шарты орындалса, онда берілген қатар...

$$жинақты

$абсолют жинақты

$шартты

$жинақсыз

$$$33 Егер және - оң сандар қатарларының мүшелеріне кез келген n үшін теңсіздігі орындалса, онда қатарының жинақсыздығынан қатарының... болуы шығады.

$$жинақсыз

$жинақты

$абсолют жинақты

$шартты жинақты

$$$34 Егер 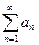-оң сандар қатары үшін шарты орындалса, онда берілген қатар...

$$жинақты

$абсолют жинақты

$шартты жинақты

$жинақсыз

$$$35 Егер 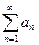-оң сандар қатары үшін шарты орындалса, онда берілген қатар....

$$жинақсыз

$жинақты

$абсолют жинақты

$шартты жинақты

$$$36 Таңбалары ауыспалы сан қатары жинақты болуы үшін оның жалпы мүшесінің шегі нолге ұмтылуы жеткілікті бола ма?

$$жоқ

$жеткілікті

$әртүрлі

$жеткілікті

$$$37 Таңбалары ауыспалы сан қатары жинақты болуы үшін оның мүшелерінің абсолют шамаларының кемуі жеткілікті бола ма?

$$жоқ

$жеткілікті

$әртүрлі

$жеткілікті

$$$38 Егер -таңбалары айнымалы сан қатары мүшелерінің абсолют шамаларынан құралған қатар жинақты болса, онда берілген қатар...жинақты

$$абсолют

$жинақсыз

$жинақты

$шартты

$$$39 Егер 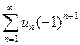- таңбалары ауыспалы сан қатары мүшелерінің абсолют шамаларынан құралған қатар жинақсыз болса, онда берілген қатар...жинақты.

$$шартты

$абсолют

$жинақсыз

$жинақты

$$$40 Мүшелері х айнымалысының функциясы болатын түріндегі қатарды... қатар деп атайды.

$$функционалдық

$сандық

$дәрежелік

$тізбек

$$$41 Мүшелері х аргументінің дәрежелік функциялары болатын 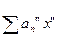немесе 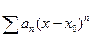түріндегі функционалдық қатарларды.... қатар деп атайды.

$$дәрежелік

$сандық

$тізбек

$тригонометриялық

$$$42 Функцияны дәрежесі бойынша дәрежелік қатар түрінде көрсету функцияны...қатарына жіктеу деп атайды.

$$Тейлор

$дәрежелік

$сандық

$Маклорен

$$$43 Егер Тейлор қатарына жіктеу нүктесінің маңайында болса, онда мұндай қатарды.... қатары деп атайды.

$$Маклорен

$дәрежелік

$сандық

$Тейлор

$$$44 Егер 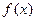-функциясы [- ] кесіндісінде жұп функция болса, онда оның Фурье қатарына жіктелуінде тек.... болады.

$$косинустар

$синустар

$тангенс

$сандар

$$$45 Егер 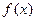- функциясы (- ) аралығында тақ функция болса, онда оның Фурье қатарына жіктелуінде тек... болады.

$$синустар

$косинус

$тангенс

$сандар

$$$46 функциясының аралығында Фурье қатарына жіктелуінде....коэффициенттері нолге тең.

$$b_n

$a_n

$а

$b

$$$47 функциясының аралығында Фурье қатарына жіктелуінде....коэффициенттері нолге тең.

$$a_n

$b_n

$а

$b

$$$48 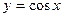функциясының аралығында Фурье қатарына жіктелуінде тек....болады.

$$косинус

$синустар

$тангенс

$сандар

$$$49 функциясының аралығында Фурье қатарына жіктелуінде тек....болады.

$$синустар

$косинус

$тангенс

$сандар

$$$50 Есептеңіз:

$$29

$-7

$40

$35

$$$51 Есептеңіз:

$$

$

$

$

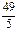
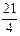
$$$52 Есептеңіз:

$$

$0,45

$

$

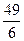
$$$53 Есептеңіз: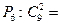

$$20

$15

$49

$

$$$54 Теңдеуді шешіңіз: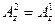

$$2

$3

$45

$0

$$$55 Есептеңіз: =

$$35

$20

$10

$0

$$$56 Теңдеуді шешіңіз

$$5

$6

$7

$0

$$$57 Есептеңіз:

$$72

$14

$48

$15

$$$58 Абонент телефон нөмірінің соңғы екі цифрын ұмытып қалды ,бірақ олардың әртүрлі екенін біледі.Таңдамай кез келген екі цифрды тере салды. Сонда керекті цифрлардың терілуінің ықтималдығын табыңдар.

$$

$

$

$

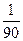
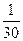
$$$59 Бірдей төрт қағаздың әрқайсысында Я,С,И,А әріптерінің біреуі жазылған. Сонда осы әріптерді таңдамай АСИЯ сөзінің шығу ықтималдығын табыңдар.

$$

$

$

$

$$$60 Теңгені екі рет лақтырғанда екі рет герб түсу ықтималдығын табыңдар.

$$0,25

$0,5

$0,125

$0

$$$61 Теңгені екі рет лақтырғанда екі рет цифр түсу ықтималдығын табыңдар.

$$0,25

$0,5

$0,125

$0

$$$62 Теңгені екі рет лақтырғанда бір рет цифр жағы түсу ықтималдығын табыңдар.

$$0,5

$0,25

$0,125

$0

$$$63 Жәшіктегі 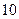деталдың екеуі жарамсыз. Таңдамай алынған үш деталдың үшеуі де жарамды болу ықтималдығын табыңдар.

$$

$

$

$

$$$64 Жәшіктегі 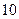деталдың екеуі жарамсыз. Таңдамай жәшіктен алынған үш деталдың екеуі жарамсыз болу ықтималдығын табыңдар.

$$

$

$

$

$$$65 Жәшіктегі 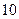деталдың екеуі жарамсыз. Таңдамай алынған үш деталдың біреуі жарамсыз болу ықтималдығын табыңдар.

$$

$

$

$

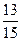
$$$66 Абонент телефон нөмірінің соңғы цифрын ұмытып қалды да, таңдамай тере салды. Сонда керекті цифрдың терілуінің ықтималдығын табыңдар.

$$0,1

$0,2

$0,25

$0,125

$$$67 Қорапта 6 қара, 3 ақ шарлар бар. Қораптан алынған 4 шардың екеуі ақ шар болуы ықтималдығын табыңдар.

$$

$

$

$

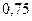
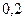
$$$68 Қорапта 6 қара, 3 ақ шарлар бар. Қораптан таңдамай бірінші алынған шардың қайтадан қорапқа салынбайды/ ақ болу, екінші алынған шардың қара болу ықтималдығын табыңдар.

$$

$

$

$

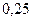
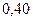
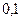
$$$69 Қорапта 6 қара, 3 ақ шарлар бар. Қораптан таңдамай бірінші алынған шардың (қайтадан қорапқа салынбайды) қара болу, екінші алынған шардың ақ болу ықтималдығын табыңдар.

$$

$

$

$

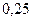
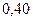
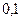
$$$70 Абонент телефон нөмірінің соңғы үш цифрын ұмытып қалды да, осы үш цифрдың әртүрлі екендігін есте сақтай отырып, таңдамай тере салды. Сонда керекті цифрлардың терілуінің ықтималдығын табыңдар.

$$

$

$

$

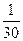
$$$71 оқиғалары толық топ құрады және . Табу керек: .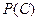

$$

$

$

$

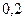
$$$72 Екі тәуелсіз оқиғалардың әрқайсысының пайда болу ықтималдықтары сәйкес 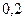және 0,8-ге тең. Тек бір ғана оқиғаның пайда болу ықтималдығын табыңдар.

$$

$

$

$

$$$73 Екі тәуелсіз оқиғалардың әрқайсысының пайда болу ықтималдықтары сәйкес 0,2 және 0,8-ге тең. Ең болмағанда бір оқиғаның пайда болу ықтималдығын табыңдар.

$$0,84

$0,1

$0,6

$0,16

$$$74 Табу керек: М(Х + У), егер М(Х)=4 и М(У)=7

$$11

$3

$25

$0

$$$75 Х кездейсоқ шамасы келесі үлестірім заңымен берілген :

Табу керек: М(х)

$$4,6

$4

$5

$0,5

$$$76 Х кездейсоқ шамасы келесі үлестірім заңымен берілген :

Табу керек: М(x)

$$3,7

$0,40

$2,20

$2,21

$$$77 Х кездейсоқ шамасы келесі үлестірім заңымен берілген :

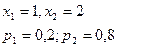Табу керек :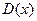

$$0,16

$0,40

$2,20

$2,21

$$$78 Х кездейсоқ шамасы келесі үлестірім заңымен берілген:

Табу керек:

$$0,40

$0,45

$2,20

$2,21

$$$79 Х, У кездейсоқ шамалары келесі үлестірім заңымен берілген :

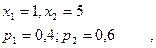
Табу керек: М(х+у)

$$4,7

$5

$7

$8,3

$$$80 n тәжирибе жасағанда оқиғаның к рет пайда болу ықтималдығын анықтайтын Бернулли формуласын көрсетіңдер:

$$

$

$

$ дұрыс жауабы жоқ

$$$81 Дискретті кездейсоқ шаманың математикалық үміті 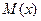қандай формуламен есептеледі?

$$

$

$

$дұрыс жауабы жоқ

$$$82 Х кездейсоқ шаманың дисперсиясы қандай формуламен табылады?

$$

$

$

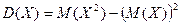
$D(X)= -M(X )

$$$83 Үлестірім заңымен белілген Х дискретті кездейсоқ шаманың математикалық үмітін табындар

x 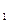=-1, x =2, x =4

p 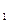=0,4, p =0,5, p =0,1

$$

$

$

$

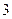
$$$84 орта квадраттық ауытқуды қандай формуламен табады:

$$

$

$

$

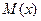
$$$85 Үлестірім заңымен берілген Х дискретті кездейсоқ шаманың дисперсиясын табыңдар:

x 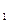=-1, x =2, x =4