Управление водной системой

Рассмотрим теперь более сложный пример управления водной системой [50], в которой учтено 12 переменных: емкость трех водохранилищ, мощности двух электростанций, распределение рабочей емкости и мертвого объема в водохранилище, питающем одну из электростанций, распределение резервной системы для регулирования паводков в трех других водохранилищах и ежегодная требуемая отдача воды для ирригации и энергетики. Структура этой системы представлена на рис. 12.5.

Введем следующие обозначения:

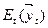– валовая прибыль в t-м году, получаемая при определенной стратегии управления ресурсами как функция от вектор-функции 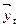, компонентами которой являются различные факторы, влияющие на величину прибыли: запроектированные параметры в системе дамб, турбогенераторов и оросительных каналов и т.д.;

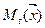– затраты, связанные с эксплуатацией, ремонтом или заменой оборудования в t-м году, как функция от вектор-функции ;

K – первоначальные капиталовложения на создание системы водных сооружений и подготовку оборудования.

Вкладывая деньги в какое-либо предприятие, следует сравнить доход, получаемый при различных вариантах политики, с доходом, получаемым от вложения той же суммы денег в банк под ежегодный процент. Учитывая формулу сложного процента, т. е. используя дисконтный множитель , получим следующие выражения для экономической эффективности многоцелевой системы водных ресурсов, эксплуатируемой в течение T лет:

(12.10)

где 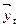= у_t, = х.

Анализируя формулу (12.10), заметим, что поскольку в знаменателе стоит величина , вклад Е_t(у_t) - М_t(х) в R оказывается тем меньшим, чем позже получена прибыль. Отсюда следует, что нет никакого смысла сохранять ресурсы для будущего и что оптимальной всегда будет политика наиболее интенсивной эксплуатации ресурсов без чрезмерного увеличения величины М_t(х). Другими словами, уравнение (12.10) оправдывает уничтожение всех естественных ресурсов в максимально короткий срок, ограниченный лишь экономическими и технологическими возможностями. Естественный путь – ввести наряду с уравнением (12.10) ограничения (граничные условия), чтобы исключить случаи, когда ежегодно изымаемое количество ресурсов данного типа превышает величину их максимальной величины, сохраняющей устойчивость всей системы. Заметим, что эти ограничения – постоянный источник конфликтов всех заинтересованных групп пользователей.

Одновременно можно учесть и экономические, и биологические факторы, если ввести первые непосредственно в показатель R, а вторые – в граничные условия.

Рассмотрим сначала метод оценки функции Е_t(у_t). Во многих случаях прибыль можно рассчитать непосредственно в денежных единицах. Ежегодный доход от орошения земель, постройки электростанций или плотин можно определить, найдя такие элементы вектора у_t, как:

y₁ – урожай, собранный с орошаемой площади;

y₂ – количество электроэнергии;

y₃ – ущерб, причиняемый паводками, которого удалось избежать в результате постройки плотин, и т.д.

Дальше можно вычислить посредством моделирования на ЭВМ доходность различных членов в течение T лет с использованием показателя R. Затем выбрать проект, который соответствует максимальному значению R и совместим с граничными условиями (ограничениями); последние диктуются необходимостью сохранения естественных ресурсов и желанием использовать их не только для получения электроэнергии или орошения, но и для организации отдыха населения.

Различные способы математического анализа и моделирования рассматриваемой водной системы описаны в работе Мааса [50], в которой перечислены основные этапы исследования. В результате исследования была создана программа для моделирования этой сложной системы. Это следующие этапы:

1. Вначале была схематически описана структура системы в целом (рис. 12.5) и найдены аналогичные случаю одного водохранилища математические уравнения, устанавливающие внутренние функциональные связи между отдельными ее частями. Эти взаимосвязи таковы:

2. Были заданы правила работы системы. В частности, с февраля по август система работает следующим образом:

§ вода выпускается из водохранилища С до тех пор, пока не будет достигнута заданная отдача, соответствующая предельной пропускной способности станции G, или водохранилище С не опорожнится;

§ та же операция повторяется по отношению к водохранилищу D;

§ если возможно, назначается дополнительный пропуск из водохранилища А до тех пор, пока не будет достигнута заданная отдача, соответствующая предельной пропускной способности станции G, или водохранилище А не опорожнится;

§ если это возможно, отбирают дополнительное количество воды из водохранилища В до тех пор, пока не будет достигнута заданная отдача, соответствующая предельной

§ пропускной способности станций В и G, или в водохранилище В не останется только мертвый объем;

§ специально предусматривается емкость для регулирования паводков в апреле, мае и июне;

§ в течение марта, апреля и мая вода от отработки резервной емкости пропускается через турбины электростанций В и G до их полной пропускной способности, а вода из водохранилища В обеспечивает требуемую отдачу для ирригации.

Рассмотренная функциональная модель – лишь одна из многих, изученных с помощью этой методики. Она показывает, что для создания компьютерной программы, позволяющей изучать различные стратегии управления, необходим огромный объем информации и детальное знание процессов принятия решений.

Контрольные вопросы

1. Каковы основные этапы системного анализа? Дайте их краткое описание.

2. Как вы понимаете обратную связь? Приведите примеры положительной и отрицательной обратной связи.