Схемы замещения двухобмоточного трансформатора, физическое толкование ее параметров.

Для уравнений приведенного трансформатора в установившемся режиме (28)—(30) может быть предложена электрическая схема замещения (рис. 5). Действительно, если представить, что к выводам вторичной обмотки подключена нагрузка , то Решая совместно (28)—(30), получаем

(35)

Нетрудно убедиться, что, согласно схеме замещения трансформатора, напряжение на первичной обмотке определяется по (35).

.

В схеме замещения имеется электрическая связь между первичной и вторичной обмотками, что позволяет исключить из рассмотрения магнитные связи.

В (21) и (28)—(30) потери в магнитопроводе не учитываются. Их можно приближенно учесть, увеличив активное сопротивление первичной обмотки r₁ или введя в z_о активное сопротивление r_о, эквивалентное потерям в стали:

z₀=r₀+jx₀, (2.36)

где магнитные потери (потери в стали)

(37)

Потери в стали пропорциональны . Так как Ф_m~ Е, потери в стали пропорцио­нальны Ф_m или B². Если не учитывать падение напряжения на z₁, потери в стали можно, с большой точностью, считать пропорциональными квадрату напряжения .

Т-образную схему замещения (рис.7) можно видоизменить, предста­вив ветвь намагничивания состоящей из двух сопротивлений (рис.8). Из схемы замещения рис.8

(38;39)

На схеме рис. 8 параметры намагничивающего контура r₁₂ и jx₁₂ представлены в виде сосредоточенных параметров. В действительности они распределенные. Используя выражения (38) и (39), можно прийти к схеме, в которой активное и реактивное сопротивления намагничиваю­щего контура соединены последовательно (рис. 9). В этой схеме замещения , , .В схему рис.9 вхо­дят активные сопротивления первичной и вторичной обмоток , индуктивные сопротивления рассеяния первичной и вторичной обмоток , а также сопротивление, эквивалентное потерям в стали, r₁₂ и со противление взаимной индукции x₁₂.

Уравнения установившегося режи­ма, векторная диаграмма и схема заме­щения позволяют проанализировать ра­боту трансформатора в установившемся режиме.

Когда z_n=:, имеет место холо­стой ход трансформатора ( ). При этом трансформатор потребляет из сети ток холостого хода, который идет на создание поля в трансформаторе и покрытие потерь в стали. Ток холостого хода имеет в основном реактивную составляющую.

При нагрузке во вторичной обмотке протекает ток , который растет при увеличении нагрузки. В первичной обмотке при увеличении нагрузки также растет ток , при этом токи и , имеют встречное направление и их сумма, практически, не изменяется [см. (30)]. Это хорошо видно и на векторной диаграмме (см. рис.2), которая является геометрической интерпретацией уравнений трансформатора. Ток холостого хода 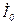при нагрузке не растет и даже уменьшается за счет падения напряжения на первичной обмотке. При изменении нагрузки во вторичной обмотке изменяется потребляемая из сети мощность в первичной обмотке, а поток Ф_m в трансформаторе почти не изменяется, так как из векторной диаграммы и схемы замещения видно, что и ( ) почти не изменяются, так как падение напряжения на первичной обмотке мало.

При емкостной нагрузке реактивная мощность в трансформатор поступает с выводов вторичной обмотки. При реактивная мощность из сети 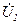не поступает, а реактивная мощность для создания поля трансформатора поступает из сети .

При увеличении емкости во вторичной обмотке реактивная мощность не только идет на создание поля в трансформаторе, но и поступает в сеть .

Для того чтобы из сети , активная мощность поступала в сеть , необходимо, чтобы . При этом на векторной диаграмме (рис.2, а)при активно-индуктивной и активной нагрузках .

Т-образная схема замещения трансформатора состоит из трех сопротивлений z₁, z^/₂ и z₁₂ , в которые входят активные и индуктивные сопротивления. Определение параметров — сопротивлений схемы замещения — может быть проведено опытным и расчетным путями.

ВОПРОС 5

Определение параметров трансформаторов путём проведения опытов холостого хода и короткого замыкания

Для определения параметров схемы замещения необходимо провести два опыта — холостого хода и короткого замыкания. При определении параметров расчетным путем рассматривают режимы холостого хода и короткого замыкания.

Холостой ход трансформатора. Уравнения трансформатора при холостом ходе, когда ∞, выглядят следующим образом: ; (40)

; (41)

; (42)

Векторная диаграмма трансформатора при холостом ходе показана на рис. 10 Схема замещения при холостом ходе может быть получена из Т-образной схемы, если

.

В опыте холостого хода снимаются зависимости тока холостого хода I_x потерь холостого хода от напряжения (рис. 13).

Сопротивление взаимной индукции

(43)

Зная полное сопротивление и , определяют

(44)

Активные сопротивления первичной и вторичной обмоток трансформатора r₁ и r₂^/ находятся опытным путем при питании обмоток постоянным током. Активные, или, вернее, омические, сопротивления находят делением постоянного напряжения на ток.

Сопротивления схемы замещения трансформатора z_о , х_о , r_о зависят от напряжения. С ростом U_x из-за насыщения z_о и х_о уменьшаются и ток увеличивается. Насыщение в трансформаторе — индукция В_т — зависит от приложенного к обмоткам напряжения U_ф, числа витков фазы обмотки пи и сечения магнитопровода S: U_ф = 4,44fВ_mSω.

Потери в стали пропорциональны В² и частоте f^1,3 приближенно. Чтобы уменьшить потери в стали, надо уменьшать в первую очередь индукцию в стержнях и ярмах магнитопровода трансформатора.

Из опыта холостого хода определяют коэффициент трансформации как отношение напряжений на первичной и вторичной обмотках при холостом ходе:

(45)

Индуктивные сопротивления в схеме замещения, найденные экспериментально при опыте холостого хода, можно использовать при напряжении, близком к тому, при котором они найдены, так как они зависят от насыщения.

Опыт короткого замыкания. Опыт проводится при пониженном напряжении, приложенном к первичной обмотке, и замкнутой накоротко вторичной обмотке (см. рис.12).

При этом , а токи примерно равны

Уравнения при коротком замыкании:

Так как намагничивающий ток 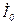при пониженном напряжении небольшой, в опыте короткого замыкания можно считать, что , откуда следует, что

Характеристики короткого замыкания показаны на рис.14. В опыте короткого замыкания трансформатор ненасыщен, поэтому ток I_к при увеличении напряжения изменяется по линейному закону. Потери при коротком замыкании пропорциональны квадрату тока. Коэффициент мощности остается постоянным при изменении напряжения, так как соотношение между активной и реактивной составляющими остается, практически, неизменным.

Из опыта короткого замыкания

Потери при коротком замыкании — это потери в меди. Потери короткого замыкания можно найти по формуле

(51)

где

В теории трансформаторов важное значение имеет понятие о напряжении короткого замыкания. Напряжение короткого замыкания u_к — это такое напряжение, при котором в опыте короткого замыкания в обмотках трансформатора протекают номинальные токи.

Напряжение короткого замыкания определяется по следующей формуле:

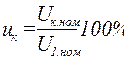, (52)

где , а z_к— сопротивление короткого замыкания при температуре 75 °С.