Зависимость проницаемости от пористости

Теоретически доказано, что для хорошо отсортированного, окатанного, однородного материала (например, кварцевый мономиктовый песок, представленный на 90 % одним минералом) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются и более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеальной пористой среды можно оценить из соотношений законов Пуазейля и Дарси.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через пористую среду, которая представляется в виде системы прямых трубок одинакового сечения длиной (L), равной длине пористой среды:

, (1.25)

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давления.

Коэффициент пористости среды, через которую проходит фильтрация, можно представить следующим образом:

. (1.26)

С учетом 1.26, уравнение 1.25 можно переписать следующим образом:

, (1.27)

и сравнить его с уравнением Дарси ( ).

Приравняв правые части уравнений, после сокращения подобных членов получим выражение для взаимосвязи проницаемости, пористости и радиуса порового канала:

. (1.28)

Выражение 1.28 используется при проведении прогнозных и модельных расчетах коэффициента проницаемости для образцов кернового материала с известной пористостью. Измерения показали, что радиусы пор, по которым в основном происходит движение жидкостей, находится в пределах от 5 до 30 мкм.

Из уравнения 1.28 следует, что радиус (размер) порового канала можно оценить:

. (1.29)

Если выразить проницаемость в мкм², то радиус поровых каналов (в мкм) будет рассчитываться по выражению:

. (1.30)

Уравнения 1.28-1.30 характеризуют взаимосвязь между пористостью, проницаемостью и радиусом порового канала и справедливы только для идеальной пористой среды, например, для кварцевого песка.

Для реальных коллекторов оценка радиуса порового канала производится с учётом структурных особенностей порового пространства пород. Обобщенным выражением для этих целей является эмпирическое уравнение Ф.И. Котяхова:

, (1.31)

где r – радиус пор;

j – структурный коэффициент, учитывающий извилистость порового пространства.

Значение j оценивают для модельных сред путём измерения электрического сопротивления пород. Для керамических, пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

. (1.32)

Для оценки взаимосвязи коэффициента проницаемости от радиуса порового каналапри фильтрации жидкости только через каналы, капилляры (поры круглого сечения) используются соотношения уравнений Пуазейля и Дарси:

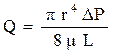и . (1.33)

Причем, пористая среда представляет собой систему трубок. Общая площадь пор, через которые идет фильтрация флюидов, оценивается как:

F = π·r². Величину π можно представить как → π = F/r². Подставив эту величину в уравнение Пуазейля (1.33, левое выражение) и сократив одинаковые параметры в выражениях (1.33, левом и правом) получим корреляционную взаимосвязь между коэффициентом проницаемости породы от радиуса порового канала:

.(1.34)

Если r измеряется в [см], а коэффициент проницаемости в [Д] (1Д ≈ 1,02·10^–8 см² или =1,01327), то вводится соответствующий коэффициент пересчета 9,869·10^–9. Тогда, коэффициент проницаемости при фильтрации жидкости через капилляр оценивается эмпирическим выражением:

k_пр =r²/(8·9,869·10^–9) = 12,5 · 10⁶ ×r².(1.35)

Оценка взаимосвязи коэффициента проницаемости от высоты поровой трещиныпри фильтрации жидкости только через трещиноватые поры оценивается из соотношений уравнений Букингема и Дарси.

Потеря давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

, (1.36)

где h – высота трещины;

v – линейная скорость фильтрации жидкости.

Выразив из уравнения Дарси величину перепада давления (∆P = v·μ·L/k_пр.), приравняв правые части с 1.36 и сократив одинаковые параметры получим выражение:

. (1.37)

С учетом того, что h измеряется в [см], а коэффициент проницаемости в [Д], вводится соответствующий коэффициент пересчета = 9,869·10^–9. Тогда, коэффициент проницаемости при фильтрации жидкости через трещину оценивается:

k_пр =h²/(12 · 9,869·10 ^–9) = 84,4 · 10⁵·h².(1.38)

Уравнения 1.35 и 1.38 используется для теоретической оценки коэффициентов проницаемости для конкретного вида пор.

Рассмотрим пример.Через кубик породы размером 10·10·10 см, с проницаемостью 10 мД фильтруется жидкость при линейной режиме вязкостью 1 спз, при градиенте давления (∆Р/∆L), равном 0,25 атм/м (0,0025 атм/см). Определить дебит?

Решение. Рассмотренный случай – субкапиллярной фильтрации, то есть фильтрация равномерная и проходит через всю площадь образца, имеющего субкапиллярную пористость. Дебит (Q₁)составит:

= 100 · 0,01 · (0,0025 /1) = 0,0025 см³/сек.

Если в этом кубике будет один канал диаметром 0,2 мм той же длины, что и кубик, то при том же градиенте давления дебит фильтрующейся жидкости через этот канал будет:

= 12,5 · 10⁶· (0,02 /2)² · π · (0,02 /2)² · 0,00025 = 0, 001 см³ /сек

Следовательно, при наличии в кубике одного канала и субкапиллярной пористости, т. е. при наличии неравномерной фильтрации суммарный дебит (Q₃) фильтрующейся жидкости составит:

Q₃ = Q₂ + Q₁ = 0,001 + 0,0025 = 0,0035 (см³/сек).

Суммарный дебит (Q₃) имеет величину на 40 % больше чем при субкапиллярной фильтрации (Q₁).

Если в кубике вместо канала имеется трещина высотой 0,2 мм и шириной 10 см, ее влияние на общий дебит жидкости, фильтрующийся через породу, будет существенным:

= (84,4 ·10⁵ · (0,02)² · 0,02 · 10 · 0,0025) / 1 = 1,688 см³/сек.

А суммарный дебит (Q₅) с учетом субкапиллярной фильтрации (Q₁) составит:

Q₅ = Q₄ + Q₁ = 1,688 + 0,0025 = 1,6905 (см³/с).

По сравнению с первым случаем дебит увеличится в 675 раз.

Пример свидетельствует о большом влиянии наличия каналов и особенно трещин в породе на объём фильтрующейся жидкости.

На практике проницаемость породы определяют в лабораторных условиях по керновому материалу (см. лабораторный практикум).