Электродвижущая сила катушки

Вращающееся магнитное поле, сце­пляясь с катушками обмотки статора, наводит в них ЭДС. Мгновенное значе­ние ЭДС (В) одной катушки с числом витков ω_k

e_k= B_δ 2 l ν ω_k , (7.3)

где В_δ — магнитная индукция в воздушном зазоре между статором и ротором электрической машины, Тл;

ν = πD₁n₁ /60 = τ2рn₁ /60 = 2τ f₁ (7.4)

- линейная скорость движения магнитного поля относительно неподвижной катушки, м/с; πD₁ = τ 2р — длина поверхности рас­точки статора. С учетом (7.4) мгновенное значение ЭДС

катушки

e_k = В_δ 4τ l f₁ w_k (7.5)

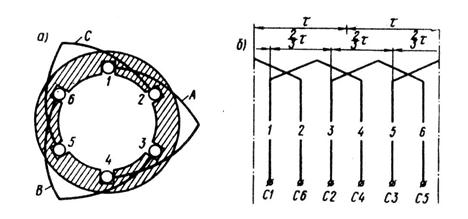
Рис. 7.4. Сосредоточенная трехфазная обмотка:

а — расположение катушек в пазах статора; б — развернутая схема обмотки

Как уже отмечалось, форма кривой ЭДС е_к зависит исключи­тельно от графика распределения индукции В_δ в воздушном зазо­ре. Однако даже при неравномерном зазоре (см. рис. 6.2) график индукции остается несинусоидальным. Поэтому ЭДС катушки е_к также несинусоидальна и наряду с первой (основной) синусои­дальной гармоникой ЭДС содержит ряд высших синусоидальных гармоник.

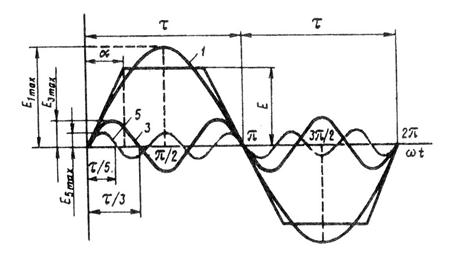
Рис. 7.5. Разложение трапецеидальной кривой ЭДС в гар­монический ряд

В связи с тем что кривая ЭДС симметрична относительно оси абсцисс, она содержит лишь нечетные гармоники (1, 3, 5 и т. д.). С некоторым приближением, приняв форму кривой ЭДС е трапецеидальной (рис. 7.5), можно записать следующее выражение гармо­нического ряда:

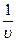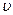
e = (sin sin ω₁t + ₂ sin 3 sin 3 ω₁t + ₂ sin 5 sin 5ω₁t + … + ₂ sin sin 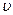ω₁t), (7.6)

где 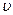— номер гармоники; ω₁, — угловая частота основной гармоники.

Из (7.6) видим, что с ростом номера гармоники ее амплитуда уменьшается пропорционально величине

sin 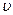/ 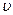² , а частота f 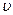= f₁ 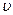, т. е. растет пропорционально номеру гармоники. Поэтому прак-

тическое влияние на форму кривой ЭДС оказывают гармоники не выше седьмой. Таким, образом задача получения в обмотке статора синусоидальной ЭДС сводится к устранению или

мучительному ослаблению высших синусоидальных гармоник, в первую очередь третьей, пятой и седьмой.

Из § 1.10 известно, что токи и ЭДС третьей гармоники во всех фазах трехфазной обмотки совпадают во времени (по фазе). Поэтому в линейной ЭДС (напряжении) при схемах соединения об­моток звездой или треугольником третья гармоника отсутствует. Все, что касается третьей гармоники, распространяется и на выс­шие гармоники ЭДС, номера которых кратны трем (9, 15 и т. д.).

Рассмотрим вопрос о возможности устранения или значитель­ного ослабления гармоник выше третьей, главным образом пятой или седьмой. Допустим, что кривая распределения магнитной

и наряду с первой гармоникой В₁ содержит пятую В₅ (рис. 7.6, а). Если при этом об­мотка выполнена с диаметральным шагом (у₁ = τ ), то ЭДС первой и пятой гармоник (е₁ и е₅) в обеих сторонах катушки (витка) (рис 7.6, 6) складываются арифметически. В этом случае результирующая ЭДС катушки е_к.л, а следовательно, и ЭДС всей обмотки наряду с пер- вой содержат и пятую гармонику.

Если же шаг катушки укоротить на полюсного деления, т. е. принять его равным

y₁ = ( 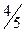)τ = 0,8τ,

Рис. 7.6. Укорочение шага обмотки на 1/5τ

то ЭДС пятой гармоники е₅, хотя и наводятся в пазовых сторонах катушки, будут находиться в противофазе относительно друг друга. В итоге сумма этих ЭДС в катушке будет равна нулю (рис. 7.6, в ) и ЭДС катушки будет содержать лишь первую (основную) ЭДС е₁ т. е. она станет практически синусоидальной. Аналогично, для уничтожения ЭДС седьмой гармоники тре­буется укорочение шага катушки на 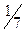, полюсного деления τ, т. е. принимаем шаг катушки равным y₁ = ( 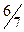)τ = 0,857τ.

Отношение шага у₁ к полюсному делению называют относи­тельным шагом обмотки = y₁/ τ Обычно относительный шаг принимают Р = 0,80 ÷ 0,89, что обеспечивает значительное ослабле­ние ЭДС высших гармоник.

Из построений, приведенных на рис. 7.6, видно, что уменьше­ние шага катушки на величину относительного укорочения ε = 1 - β вызывает ослабление не только ЭДС высших гармоник,

но и ЭДС первой (основной) гармоники. Объясняется это тем, что при диаметральном шаге (у₁ = τ) ЭДС первой гармоники Е_1к.д (рис. 7.6, б) равна арифметической сумме ЭДС, наводимых в пазовых сторонах катушки (Е_1к.д = 2Е₁), а при укорочении шага на величину ε (рис. 7.6, в) ЭДС в пазовых сторонах катушки оказываются сдви­нутыми по фазе относительно друг друга на угол ε·180° и ЭДС катушки Е_1к.у определяется геометрической суммой:

Е_1к.у = Е₁ + Е₁ cos (ε·180°) < Е_1к.д . (7.7)

Уменьшение ЭДС катушки при укорочении ее шага на вели­чину ε = 1 - β учитывается коэффициентом укорочения шага k_y = Е_ку / Е_кд . Для первой гармоники

k_yl = sin(β· 90°). (7.8)

Для ЭДС любой гармоники

k_yυ = sin(υβ · 90°). (7.9)

Ниже приведены значения коэффициентов укорочения k_yυ в зависимости от относительного шага β обмотки для различных гармоник ЭДС:

В заключение следует отметить, что укорочение шага обмотки по пазам возможно лишь в двухслойных обмотках (см. § 7.1). Однослойные обмотки выполняются с диаметральным ша- гом, поэтому ЭДС, наводимые в них, содержат в значительной мере высшие гармоники 5-го и

7-го порядка. Это ограничивает применение однослойных обмоток в асинхронных двигателях мощностью более 15 - 22 кВт.