
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основное уравнение МОБ
Данные МОБ можно применять при экономико-математических ме-'тодах исследования межотраслевых связей. Это означает, что количественное выражение экономических связей каждой отрасли с другими отраслями может быть представлено в виде системы линейных уравнений. МОБ имеет следующий вид:
| Промежуточное потребление (отрасли) | Конечное использование | Всего использовано | ||||||
| I | … | j | … | n | ||||
| Проме-жуточное потреб-ление | l | allxl | … | aljxj | … | alnxn | yl | xl |
| … | … | … | … | … | … | … | … | |
| i | ajlxl | … | aijxj | ainxn | yi | xi | ||
| … | … | … | … | … | … | … | … | |
| n | anlxl | … | anjxj | … | annxn | yn | xn | |
| Валовая добавленная стоимость | zl | … | zj | … | zn | |||
| Всего ресурсов | xl | … | xj | … | xn |
Если рассматривать данные МОБ по строкам, то каждую отрасль можно описать в виде следующего уравнения:

где хi — продукция i-й отрасли;
аij — коэффициент прямых затрат продукции i-й отрасли на единицу продукции j-й отрасли (аij = хij/хj);
хj — продукция j-й отрасли;
yi - конечный спрос i-й отрасли (конечное потребление, валовое накопление, сальдо экспорта—импорта).
Уравнение (8.1) характеризует использование продукции каждой отрасли на промежуточное и конечное потребление, накопление и другие конечные нужды.
При рассмотрении МОБ по колонкам каждая отрасль может быть представлена следующим уравнением:

где хj — продукция j-й отрасли;
zj — валовая добавленная стоимость j-й отрасли.
Уравнение (8.2) характеризует стоимостной состав выпуска продукции каждой отрасли.
В матричной форме уравнение (8.1) имеет вид:
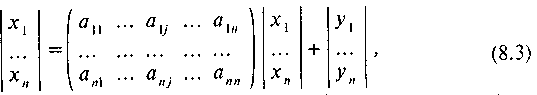
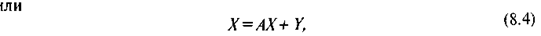
где X — вектор выпуска продукции;
A - матрица коэффициентов прямых затрат, позволяющая установить прямые производственные связи между отраслями;
Y — вектор конечного спроса.
С помощью ЭВМ на основе этой матрицы рассчитывается матрица коэффициентов полных затрат, показывающих как прямые, так и косвенные затраты на производство единицы конечной продукции.
Важнейшей особенностью матрицы коэффициентов полных затрат является то, что, если эти коэффициенты умножить на вектор конечного спроса, то можно получить выпуск продукции по каждой отрасли. Приведем математическое обоснование этого расчета.
Из формулы (8.4) вытекает, что:
Y = X — AX, (8.5)
или
Y = (E — A)X, (8.6)
где Е— единичная матрица.
Умножив обе части уравнения на (Е— А)-1, получим:
(E —A)-1 Y = (E - А)-1 (Е - А)Х, (8.7)
где (Е — А)-1 — матрица коэффициентов полных затрат.
Тогда
(Е-А)-1 Y = X. (8.8)
Уравнение (8.8) называется основным уравнением МОБ, поскольку оно может использоваться прежде всего для прогнозирования. Имея матрицу коэффициентов полных затрат и перебирая различные варианты вектора распределения конечного спроса, можно рассчитать различные варианты прогноза.
Рассмотрим построение МОБ на условном примере. Допустим, что экономика страны состоит из трех отраслей. Взаимосвязи между этими отраслями можно проследить по их счетам. В данном примере не учитывается уплата отраслями налогов.
Счет отрасли 1, млн. руб.
| Дебет | Кредит | ||
| Запасы готовой продукции на начало года Куплено материалов у отрасли 2 Куплено материалов у отрасли 3 Выплачено работникам | Получено за продукцию, проданную отрасли 2 Получено за продукцию, проданную населению Запасы готовой продукции на конец года | ||
| Всего затрат Прибыль | Всего получено | ||
| Итого 150 | Итого 150 |
Счет отрасли 2, млн руб
| Куплено материалов у отрасли 1 Выплачено работникам | Получено за продукцию, проданную отрасли 1 Получено за продукцию, проданную отрасли 3 Запасы готовой продукции на конец года | ||
| Всего затрат Прибыль | Всего получено | ||
| Итого | Итого |
Счет отрасли 3, млн. руб.
| Куплено материалов у отрасли 2 Выплачено работникам | Получено за продукцию, проданную отрасли 1 Получено за продукцию, проданную населению | ||
| Всего затрат | Всего получено Убыток | ||
| Итого | Итого |
Связи, существующие между 1, 2, 3-й отраслями, можно показать с помощью таблицы МОБ. При этом необходимо привести в соответствие номенклатуры затрат во всех счетах отраслей, что в данном примере было учтено заранее. МОБ по экономике, состоящей только из этих отраслей, имеет следующий вид (млн руб.):
| Отрасли | Промежуточное потребление | Итого | Конечное потребление | Валовое накопление | Итого | Всего | |||
| Промежуточное потребление | — | — | — . | ||||||
| — | — | ||||||||
| — | — | — | |||||||
| Итого | |||||||||
| Оплата труда наемных работников | |||||||||
| Валовая прибыль | —10 | ||||||||
| Итого | |||||||||
| Всего |
Из примера видно, что по каждой отрасли ресурсы (по колонкам) равны их использованию (по строкам).
Дата добавления: 2014-11-13; просмотров: 311; Мы поможем в написании вашей работы!; Нарушение авторских прав |