
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
P(t)³0.
Свойства плотности распределения вероятностей
непрерывной случайной величины:
1. Плотность распределения – неотрицательная функция:
p(t)³0.
Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.
2.  =1.
=1.
Учитывая, что F(+¥)=1, получаем:  =1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.
=1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.
Эти два свойства являются характеристическими для плотности распределения вероятностей. Доказывается и обратное утверждение:
Любая неотрицательная функция p(t), для которой  =1, является плотностью распределения вероятностей некоторой непрерывно распределенной случайной величины.
=1, является плотностью распределения вероятностей некоторой непрерывно распределенной случайной величины.
Общий вид графика функции плотности распределения вероятностей непрерывной случайной величины приведен на рисунке:

30. Вероятность попадания случайной величины в заданный интервал.
Зная плотность распределения, можно вычислить вероятность попадания значений непрерывной случайной величины в заданный интервал.
Вероятность того, что непрерывная случайная величина примет значения, принадлежащие интервалу (a, b), равна определенному интервалу от плотности распределения, взятому в пределах от а до b:
P(а£Х<b)=  .
.
Действительно, P(а£Х<b)=F(b) – F(a)= 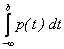 –
– 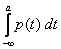 =
=  по одному из свойств определенного интеграла.
по одному из свойств определенного интеграла.
Из вышеприведенного утверждения можно сделать вывод, что вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю. Отсюда,
P(a£Х<b)=P(a<Х<b)=P(a<Х£b)=P(a£Х£b)=F(b) – F(a).
Геометрически вероятность попадания значений непрерывной случайной величины в интервал (a, b) может быть рассмотрена как площадь фигуры, ограниченной осью Ох, графиком плотности распределения p(t) и прямыми х=a и х=b.

31. Нахождение функции распределения по известной плотности распределения.
Зная плотность распределения F(X), можно найти функцию распределения F(X) по формуле
 .
.
Действительно, F(X) = P(X < X) = P(-∞ < X < X).
Следовательно,
 .
.
Или
 .
.
Таким образом, Зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения можно найти плотность распределения, а именно:
F(X) = F'(X).
Пример: Найти функцию распределения по данной плотности распределения:

Решение: Воспользуемся формулой 
Если X ≤ A, то F(X) = 0, следовательно, F(X) = 0. Если A < x ≤ b, то F(x) = 1/(b-a),
Следовательно,
 .
.
Если X > B, то
 .
.
Итак, искомая функция распределения

32. Вероятностный смысл распределения.
Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу  , приближенно равна (с точностью до бесконечно малых высшего порядка относительно
, приближенно равна (с точностью до бесконечно малых высшего порядка относительно  ) произведению плотности распределения вероятности в точке на длину интервала
) произведению плотности распределения вероятности в точке на длину интервала  :
:
 .
.
33. Закон равномерного распределения вероятностей.
Случайная величина Х называется равномерно распределеннойна отрезке [a, b], если ее плотность распределения вероятностей имеет вид:
 .
.
График плотности распределения вероятностей равномерно распределенной случайной величины представлен на рисунке.

34. Числовые характеристики непрерывных случайных величин.
Пусть непрерывная случайная величина Х задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b].
Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
Средним квадратичным отклонениемназывается квадратный корень из дисперсии.
МодойМ0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.
Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.
Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.
Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.
Начальным моментомпорядка k случайной величины Х называется математическое ожидание величины Хk.
Начальный момент первого порядка равен математическому ожиданию.
Центральным моментомпорядка k случайной величины Х называется математическое ожидание величины
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.
Для характеристики островершинности и плосковершинности распределения
Абсолютный центральный момент первого порядка называется средним арифметическим отклонением
35. Нормальное распределение, его математическое ожидание, дисперсия.
Случайная величина  называется распределенной по нормальному закону, если ее плотность вероятности имеет вид:
называется распределенной по нормальному закону, если ее плотность вероятности имеет вид:

Здесь 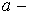 математическое ожидание,
математическое ожидание,  дисперсия,
дисперсия,  среднее квадратическое отклонение. Как и ранее,
среднее квадратическое отклонение. Как и ранее,  , однако, этот интеграл вычисляется численными методами. Чтобы упростить эту процедуру, пользуются преобразованием случайной величины
, однако, этот интеграл вычисляется численными методами. Чтобы упростить эту процедуру, пользуются преобразованием случайной величины  и правилом сохранения элемента вероятности
и правилом сохранения элемента вероятности  , где
, где 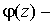 плотность распределения вероятности случайной величины
плотность распределения вероятности случайной величины  :
:
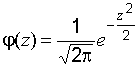 .
.
Как видим, индивидуальные числовые характеристики распределения (математическое ожидание и дисперсия) в последнее выражение не входят, т.е. вышеуказанным преобразованием нормальная случайная величина  приведена к нормальной стандартной случайной величине
приведена к нормальной стандартной случайной величине  с параметрами 0 (математическое ожидание) и 1 (дисперсия). Дифференциальная и интегральная функции стандартного нормального распределения табулированы (имеются таблицы), что существенно облегчает вычисления. Интегральная функция распределения обозначается
с параметрами 0 (математическое ожидание) и 1 (дисперсия). Дифференциальная и интегральная функции стандартного нормального распределения табулированы (имеются таблицы), что существенно облегчает вычисления. Интегральная функция распределения обозначается  ,
,

Часто используют функцию Лапласа:

Очевидны следующие свойства:


где  .
.
Пример. Нормальная случайная величина  задана математическим ожиданием
задана математическим ожиданием  и средним квадратическим отклонением
и средним квадратическим отклонением  . Записать соответствующую дифференциальную функцию, схематично изобразить ее график, вычислить вероятность попадания случайной величины
. Записать соответствующую дифференциальную функцию, схематично изобразить ее график, вычислить вероятность попадания случайной величины  в интервал
в интервал 
Решение: Записать дифференциальную функцию нормальной случайной величины  с заданными значениями математического ожидания и дисперсии значит в общее выражение для дифференциальной функции нормальной случайной величины подставить заданные
с заданными значениями математического ожидания и дисперсии значит в общее выражение для дифференциальной функции нормальной случайной величины подставить заданные  и
и  . Например, если
. Например, если  , то получим
, то получим
 .
.
При изображении этой функции на схематичном графике следует учесть, что эта функция имеет максимум при  , симметрична относительно
, симметрична относительно  (это видно непосредственно из приведенной выше формулы) и стремится к нулю при
(это видно непосредственно из приведенной выше формулы) и стремится к нулю при  . Однако правило
. Однако правило  (вероятность того, что случайная величина примет значение, по модулю отличающееся от математического ожидания на
(вероятность того, что случайная величина примет значение, по модулю отличающееся от математического ожидания на  или более, пренебрежимо мала – составляет всего около 0,0027) позволяет нам закончить правую ветвь в точке
или более, пренебрежимо мала – составляет всего около 0,0027) позволяет нам закончить правую ветвь в точке  а левую – в точке
а левую – в точке  Высота максимума в точке
Высота максимума в точке  составит
составит  Дополнительно надо учесть, что перегибы ветвей будут иметь место в точках
Дополнительно надо учесть, что перегибы ветвей будут иметь место в точках 
Вероятность попадания случайной величины  в интервал
в интервал  вычислим так:
вычислим так:

При этом следует воспользоваться таблицами функции стандартного нормального распределения  или функции Лапласа
или функции Лапласа  .
.
36. Нормальная кривая.
Центральная предельная теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
Говорят, что случайная величина Х распределена по нормальному закону с параметрами а и  , если плотность распределения вероятностей имеет вид:
, если плотность распределения вероятностей имеет вид:
 , –¥<t<¥.
, –¥<t<¥.
Вероятностный смысл параметров а и  таков: а – математическое ожидание случайной величины Х, s – среднее квадратическое отклонение величины.
таков: а – математическое ожидание случайной величины Х, s – среднее квадратическое отклонение величины.
Иногда такой закон распределения называют Гауссовским. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). На рисунке изображены нормальные кривые с параметрами а=1 и  ,
,  ,
,  .
.

Из рисунка видно, что положение пика кривых определяется параметром а=1, а параметр s (среднее квадратическое отклонение) характеризует форму нормальной кривой. При увеличении s уменьшается максимум кривой распределения, сама кривая становится более пологой, растягиваясь вдоль оси абсцисс. И, наоборот, при уменьшении s возрастает максимум кривой распределения, сама кривая становится более «островершинной». Площадь, ограниченная любой нормальной кривой и осью абсцисс, равна единице. Параметр а(математическое ожидание величины) определяет положение максимума на оси абсцисс, не влияя на форму кривой. На рисeyrt ниже показаны нормальные кривые с одинаковым средним квадратическим отклонением  и разными математическими ожиданиями а=–1, а=0, а=1.
и разными математическими ожиданиями а=–1, а=0, а=1.



Нормальное распределение с параметрами а=0 и  называется нормированным.
называется нормированным.
36. Вероятность попадания в заданный интервал нормальной случайной величины.
Вероятность того, что Х примет значение, принадлежащее интервалу (α,β)
P(α<X<β)=Ф((β-a)/σ)-Ф((α-a)/σ), где  – функция Лапласа.
– функция Лапласа.
1. Ф(-∞)=0
2. Ф(+∞)=1
3. Ф(-х)=1-Ф(х)
P(mx-l<x<mx+l)=Ф(l/σ)-Ф(-l/σ)=2Ф(l/σ)-1
38. Вычисление вероятности заданного отклонения.
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства |x —а|<d.
Заменим это неравенство равносильным ему двойным неравенством

Тогда получим:

Приняв во внимание равенство:

(функция Лапласа—нечетная), окончательноимеем
 Вероятность заданного отклонения равна
Вероятность заданного отклонения равна

На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .

Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратическое отклонение Х соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
Решение: Воспользуемся формулой

По условию ,

тогда

39. Правило трех сигм.
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от мат. ожидания не превосходит утроенного среднего квадратического отклонения.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
40. Генеральная и выборочная совокупность. Повторная и бесповторная выборки. Статическое распределение выборки.
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.
Выборочной совокупностью или просто выборкой
называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность
объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной)
называют число объектов этой совокупности.
Пример: если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а
объем выборки n =100.
Повторной называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой
отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось n1 раз, х2 – n2 раз, хk– nk раз и ∑ni=n - объем выборки. Наблюдаемые значения х1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений варианты называют частотой, а ее отношение к объему выборки - относительной частотой ni/n=wi
Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант хi и соответствующих им частот ni или относительных частот wi.
Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:
| x1 | x2 | ... | xm |
| n1 | n2 | ... | nm |
(сумма всех частот равна объему выборки ∑ni=n)
или в виде таблицы распределения относительных частот:
| x1 | x2 | ... | xm |
| w1 | w2 | ... | wm |
(сумма всех относительных частот равна единице ∑wi=1).
41. Понятие о системе случайных величин.
Если возможное значение случайной величины определяется одним числом, то она называется одномерной. Например, число очков, выпадающее при бросании кости (дискретная одномерная случайная величина), или, расстояние от орудия до места падения снаряда (непрерывная одномерная случайная величина).
Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, ..., n числами. Такие величины называются соответственно двумерными, трехмерными, . . ., n-мерными.
Двумерную случайную величину обозначают (X, Y). Каждую из величин Xи Yназывают составляющей; обе величины Xи Y, рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично n-мерную величину можно рассматривать как систему п случайных величин.
42. Функция распределения двумерной случайной величины.
Функцией распределения вероятностей системы двух случайных величин называется функция двух аргументов  , равная вероятности совместного выполнения двух неравенств
, равная вероятности совместного выполнения двух неравенств  и
и  , т. е.
, т. е.

Геометрически функцию распределения системы двух случайных величин можно интерпретировать как вероятность попадания случайной точки  в левый нижний бесконечный квадрант плоскости (рис. 14) с вершиной в точке
в левый нижний бесконечный квадрант плоскости (рис. 14) с вершиной в точке  .
.
Свойства функции распределения системы двух случайных величин:
1) Если один из аргументов стремится к + бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.
2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.
3) При стремлении одного или обоих аргументов к - бесконечности функция распределения стремится к нулю.
4) Функция распределения является неубывающей функцией по каждому аргументу.
5) Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле.

43. Двумерная плотность вероятности.
Как известно, случайная величина имеет плотность вероятности, если она непрерывна. Говоря о случайных величинах, двумерная случайная величина называется непрерывной, если ее функция распределения является непрерывной функцией. И существует вторая смешанная производная F ''xy (x,y), которая и является плотностью вероятности двумерной случайной величины.
Т.е. плотность вероятности это вторая смешанная производная от функции распределения двумерной случайной величины:
 В общем виде плотность вероятности двумерной случайной величины выражается следующей формулой
В общем виде плотность вероятности двумерной случайной величины выражается следующей формулой

| ||||||||||||||||||||||||||||
где
r - коэффициент корреляции случайных величин X и Y σx - среднее квадратическое отклонение случайной величины X σy - среднее квадратическое отклонение случайной величины Y mx- математическое ожидание случайной величины X my - математическое ожидание случайной величины Y
Если случайные величины подчинены нормальному закону распределения и не коррелированы (r = 0 ), то формула плотности вероятности примет вид:
 44. Числовые характеристики системы двух случайных величин.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.
45. Корреляционный момент. Коэффициент корреляции.
Корреляционным моментом
44. Числовые характеристики системы двух случайных величин.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.
45. Корреляционный момент. Коэффициент корреляции.
Корреляционным моментом  случайных величин случайных величин  и и  называют математическое ожидание произведения отклонений этих случайных величин: называют математическое ожидание произведения отклонений этих случайных величин:  . Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей случайных величин . Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей случайных величин  и и  . Корреляционный момент служит для характеристики связи между случайными величинами . Корреляционный момент служит для характеристики связи между случайными величинами  и и  . Теорема. Корреляционный момент двух независимых случайных величин . Теорема. Корреляционный момент двух независимых случайных величин  и и  равен нулю. Теорема. Абсолютная величина корреляционного момента двух случайных величин и не превосходит среднего геометрического их дисперсий: равен нулю. Теорема. Абсолютная величина корреляционного момента двух случайных величин и не превосходит среднего геометрического их дисперсий:  .
Коэффициентом корреляции .
Коэффициентом корреляции  случайных величин случайных величин  и и  называют отношение корреляционного момента к произведению их средних квадратических отклонений: называют отношение корреляционного момента к произведению их средних квадратических отклонений:  . Так как размерность . Так как размерность  равна произведению размерностей случайных величин равна произведению размерностей случайных величин  и и  , ,  имеет размерность случайной величины имеет размерность случайной величины  , ,  имеет размерность случайной величины имеет размерность случайной величины  , то , то  – безразмерная величина. Теорема. Абсолютная величина коэффициента корреляции не превышает единицы: – безразмерная величина. Теорема. Абсолютная величина коэффициента корреляции не превышает единицы:  .
46. Линейная регрессия.
Рассмотрим двумерную случайную величину (X,Y), где X и Y - зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X: .
46. Линейная регрессия.
Рассмотрим двумерную случайную величину (X,Y), где X и Y - зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:
 ,
где ,
где  и и  - параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них - метод наименьших квадратов.
Функцию - параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них - метод наименьших квадратов.
Функцию 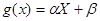 называют «наилучшим приближением» Y в смысле метода наименьших квадратов, если математическое ожидание М [Y—g(X)]2принимает наименьшее возможное значение; функцию g(x)называют среднеквадратической регрессией Y на X.
Теорема.Линейная средняя квадратическая регрессия Y на X имеет вид называют «наилучшим приближением» Y в смысле метода наименьших квадратов, если математическое ожидание М [Y—g(X)]2принимает наименьшее возможное значение; функцию g(x)называют среднеквадратической регрессией Y на X.
Теорема.Линейная средняя квадратическая регрессия Y на X имеет вид
 ,
где тх=M(X), тy=M(Y), ,
где тх=M(X), тy=M(Y),  , ,  , r = μху /(σxσy) - коэффициент корреляции величин X и Y.
Доказательство. Введем в рассмотрение функцию двух независимых аргументов , r = μху /(σxσy) - коэффициент корреляции величин X и Y.
Доказательство. Введем в рассмотрение функцию двух независимых аргументов  и и  : :
 .
Учитывая, что М (X—тх)=М (Y—my )= 0, M[(X—mx)*(Y-my)]= μху=r σxσy,
и выполнив выкладки, получим .
Учитывая, что М (X—тх)=М (Y—my )= 0, M[(X—mx)*(Y-my)]= μху=r σxσy,
и выполнив выкладки, получим
 .
Исследуем функцию .
Исследуем функцию  на экстремум, для чего приравняем нулю частные производные: на экстремум, для чего приравняем нулю частные производные:
 Отсюда
Отсюда
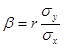 , ,  .
Легко убедиться, что при этих значениях .
Легко убедиться, что при этих значениях  и и  рассматриваемая функция принимает наименьшее значение.
Итак, линейная средняя квадратическая регрессия Y и X имеет вид рассматриваемая функция принимает наименьшее значение.
Итак, линейная средняя квадратическая регрессия Y и X имеет вид
 ,
или ,
или
 .
Коэффициент .
Коэффициент  называют коэффициентом регрессии Y наX, а прямую называют коэффициентом регрессии Y наX, а прямую
 (**)
называют прямой среднеквадратической регрессии Y на X.
Подставив найденные значения (**)
называют прямой среднеквадратической регрессии Y на X.
Подставив найденные значения  и и  в соотношение (*), получим минимальное значение функции F ( в соотношение (*), получим минимальное значение функции F (  , ,  ), равное ), равное  (1 - r2). Величину (1 - r2). Величину  (1 - r2) называют остаточной дисперсией случайной величины Y относительно случайной величины X; она характеризует величину ошибки, которую допускают при замене Y линейной функцией g(X)= (1 - r2) называют остаточной дисперсией случайной величины Y относительно случайной величины X; она характеризует величину ошибки, которую допускают при замене Y линейной функцией g(X)=  + +  X. При r = ±1 остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от X.
Итак, если коэффициент корреляции r = ± 1, то Y и X связаны линейной функциональной зависимостью.
Аналогично можно получить прямую среднеквадратической регрессии X на Y: X. При r = ±1 остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от X.
Итак, если коэффициент корреляции r = ± 1, то Y и X связаны линейной функциональной зависимостью.
Аналогично можно получить прямую среднеквадратической регрессии X на Y:
 (***)
( (***)
(  - коэффициент регрессии X на Y) и остаточную дисперсию - коэффициент регрессии X на Y) и остаточную дисперсию  (1 - r2)величины X относительно Y.
Если r = ±1, то обе прямые регрессии, как видно из (**) и (***), совпадают.
Из уравнений (**) и (***) следует, что обе прямые регрессии проходят через точку (тх, mу), которую называют центром совместного распределения величин X и Y.
47. Линейная корреляция.
Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то X и Y связаны линейной корреляционной зависимостью.
Доказательство. Двумерная плотность вероятности (1 - r2)величины X относительно Y.
Если r = ±1, то обе прямые регрессии, как видно из (**) и (***), совпадают.
Из уравнений (**) и (***) следует, что обе прямые регрессии проходят через точку (тх, mу), которую называют центром совместного распределения величин X и Y.
47. Линейная корреляция.
Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то X и Y связаны линейной корреляционной зависимостью.
Доказательство. Двумерная плотность вероятности
 , (*)
где , (*)
где  , ,  . (**)
Плотность вероятности составляющей X . (**)
Плотность вероятности составляющей X
 . (***)
Найдем функцию регрессии М (Y|х),для чего сначала найдем условный закон распределения величины Y при Х = х [см. § 14, формула (**)]: . (***)
Найдем функцию регрессии М (Y|х),для чего сначала найдем условный закон распределения величины Y при Х = х [см. § 14, формула (**)]:
 .
Подставив (*) и (**) в правую часть этой формулы выполнив выкладки, имеем .
Подставив (*) и (**) в правую часть этой формулы выполнив выкладки, имеем
 .
Заменив и и v по формулам (**), окончательно получим .
Заменив и и v по формулам (**), окончательно получим
 .
Полученное условное распределение нормально с математическим ожиданием (функцией регрессии Y на X) .
Полученное условное распределение нормально с математическим ожиданием (функцией регрессии Y на X)
 и дисперсией
и дисперсией  .
Аналогично можно получить функцию регрессии X на Y: .
Аналогично можно получить функцию регрессии X на Y:
 .
Так как обе функции регрессии линейны, то корреляция между величинами X и Y линейная, что и требовалось доказать.
Принимая во внимание вероятностный смысл параметров двумерного нормального распределения (см. § 19), заключаем, что уравнения прямых регрессии .
Так как обе функции регрессии линейны, то корреляция между величинами X и Y линейная, что и требовалось доказать.
Принимая во внимание вероятностный смысл параметров двумерного нормального распределения (см. § 19), заключаем, что уравнения прямых регрессии
 , ,  совпадают с уравнениями прямых среднеквадратической регрессии.
48. Эмпирическая функция распределения.
Эмпирической функцией выборки (функцией распределения выборки) называется функция
совпадают с уравнениями прямых среднеквадратической регрессии.
48. Эмпирическая функция распределения.
Эмпирической функцией выборки (функцией распределения выборки) называется функция
, которую можно записать в следующем виде:
Данная функция непрерывная, кусочно-постоянна и изменяется в каждой точке хi, гдехi — варианта рассматриваемого статистического распределения.
49. Полигон и гистограмма. Полигон (для дискретной случайной величины) - ломаная, соединяющая точки (хi, ni — полигон частот или точки (хi, wi) — полигон относительных частот. Полигон частот:
Гистограмма — ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются отрезки длиной xi-xi-1, а их высоты равны:
Если объем выборки из генеральной совокупности случайной непрерывной величины велик, то прибегают к предварительной группировке данных: размах выборки разбивают на k частичных интервалов Ji. Количество интервалов подсчитывается по формуле: k=log2n+1 Подсчитывается, сколько значений из n1, n2,...,nm попало в каждый из к интервалов. Вариантами для выборки считают середины этих интервалов. Эмпирической плотностью распределения выборки:
50. Статистические оценки параметров распределения. Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Смещеннойназывают оценку, математическое ожидание которой не равно оцениваемому параметру. Эффективнойназывают статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности. Состоятельнойназывают статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n→∞ стремится к нулю, то такая оценка оказывается и состоятельной.
51. Несмещенные, эффективные и состоятельные оценки. Несмещеннойназывают статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е. М (Θ*) = Θ. Смещеннойназывают оценку, математическое ожидание которой не равно оцениваемому параметру. Эффективнойназывают статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности. Состоятельнойназывают статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n→∞ стремится к нулю, то такая оценка оказывается и состоятельной. 52. Генеральная средняя. Выборочная средняя. Групповая и общая средние. Пусть изучается дискретная генеральная совокупность относительно количественного признака X. Генеральной средней Если все значения x1, х2, …, xN признака генеральной совокупности объема N различны, то
Если жезначения признака x1, х2, …, xk имеютсоответственно частоты N1, N2, ..., Nk ,причем N1 +N2+…+Nk=N ,то
т. е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам. Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема п. Выборочной средней Если все значения x1, х2, …, xn признака выборки объема n различны, то Если же значения признака x1, х2, …, xk имеют соответственно частоты n1, n2, …, nk, причем п1 + п2+… + nk = n,то или т.е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам. Групповой среднейназывают среднее арифметическое значений признака, принадлежащих группе. Теперь целесообразно ввести специальный термин для средней всей совокупности. Общей средней Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп, Пример.Найти общую среднюю совокупности, состоящей изследующих двух групп:
Решение. Найдем групповые средние:
Найдем общую среднюю по групповым средним: 53. Генеральная дисперсия. Выборочная дисперсия. Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения Если все значения x1, х2, …, xN признака генеральной совокупности объема N различны, то Если же значения признака x1, х2, …, xk имеют соответственно частоты N1, N2,…, Nk,причем N1+N2+…+Nk=N, то
т.е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам. Пример.Генеральная совокупность задана таблицей распределения xi 2 4 5 6 Ni 8 9 10 3 Найти генеральную дисперсию. Решение. Найдем генеральную среднюю:
Найдем генеральную дисперсию;
Генеральным средним квадратическим отклонением (стандартом)называют квадратный корень изгенеральной дисперсии: |
.
Выборочной дисперсией  называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  .
.
Если все значения x1, х2, …, xn признака выборки объема п различны, то
 .
.
Если же значения признака x1, х2, …, xk имеют соответственно частоты п1, n2,…, nk,причем n1 + n2+…+nk = n, то
 ,
,
т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Пример.Выборочная совокупность задана таблицей распределения
xi 1 2 3 4
ni 20 15 10 5
Найти выборочную дисперсию.
Решение. Найдем выборочную среднюю (см. § 4):
 .
.
Найдем выборочную дисперсию:
 .
.
Выборочным средним квадратическим отклонением (стандартом)называют квадратный корень из выборочной дисперсии:
 .
.
54. Формула для вычисления дисперсии.
Теорема.Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
 .
.
Доказательство. Справедливость теоремы вытекает из преобразований:

 .
.
Итак,
 ,
,
где  ,
,  .
.
Пример.Найти дисперсию по данному распределению
xi 1 2 3 4
ni 20 15 10 5
Решение.Найдем общую среднюю:
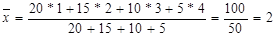 .
.
Найдем среднюю квадратов значений признака:
 .
.
Искомая дисперсия
 =5-22=1.
=5-22=1.
55. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
Точечнойназывают оценку, которая определяется одним числом. Все оценки, рассмотренные выше,- точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальнойназывают оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже).
Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной величиной). Ясно, что Θ* тем точнее определяет параметр Θ, чем меньше абсолютная величина разности |Θ - Θ*|. Другими словами, если δ>0 и |Θ - Θ*|<δ, то чем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка Θ * удовлетворяет неравенству |Θ - Θ*|<δ; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью)оценки Θ по Θ* называют вероятностьγ,с которой осуществляется неравенство |Θ - Θ*|<δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что |Θ - Θ*|<δ, равна γ:
Р[|Θ - Θ*|<δ]= γ.
Заменив неравенство |Θ - Θ*|<δ равносильным ему двойным неравенством -δ <Θ - Θ*< δ, или Θ*- δ <Θ< Θ* + δ, имеем
Р[Θ* - δ <Θ< Θ* + δ] = γ.
Это соотношение следует понимать так: вероятность того, что интервал(Θ*-δ, Θ*+δ) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.
Доверительнымназывают интервал (Θ*-δ, Θ*+δ), который покрывает неизвестный параметр с заданной надежностью γ.
56. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ.
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней  . Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью γ.
. Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью γ.
Будем рассматривать выборочную среднюю  как случайную величину
как случайную величину  (
(  изменяется от выборки к выборке) и выборочные значения признака х1, x2, ...,хn - как одинаково распределенные независимые случайные величины Х1, Х2, ...,Хn (эти числа также изменяются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно а и среднее квадратическое отклонение - σ.
изменяется от выборки к выборке) и выборочные значения признака х1, x2, ...,хn - как одинаково распределенные независимые случайные величины Х1, Х2, ...,Хn (эти числа также изменяются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно а и среднее квадратическое отклонение - σ.
Примем без доказательства, что если случайная величина X распределена нормально, то выборочная средняя  ,найденная по независимым наблюдениям, также распределена нормально. Параметры распределения
,найденная по независимым наблюдениям, также распределена нормально. Параметры распределения  таковы :
таковы :
M(  )=a,
)=a,  .
.
Потребуем, чтобы выполнялось соотношение
Р(|Х - а| < δ) = γ,
где γ - заданная надежность.
Пользуясь формулой
Р(|Х-а| < δ) = 2Ф(δ/σ),
заменив X на  и σ на
и σ на  , получим
, получим
Р(|Х-а|) <δ) = 2Ф(δ  ) = 2Ф (t),
) = 2Ф (t),
где t = δ  .
.
Найдя из последнего равенства  , можем написать
, можем написать
Р (|  —а | <
—а | <  ) = 2Ф(t).
) = 2Ф(t).
Приняв во внимание, что вероятность P задана и равна γ, окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю вновь обозначим через  )
)

Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал (  ,
,  ) покрывает неизвестный параметр а; точность оценки
) покрывает неизвестный параметр а; точность оценки  .
.
Итак, поставленная выше задача полностью решена. Укажем еще, что число t определяется из равенства 2Ф(t) = γ. или Ф(t)= γ /2; по таблице функции Лапласа (см. приложение 2) находят аргумент t, которому соответствует значение функции Лапласа, равное γ /2.
57. Условные варианты.
Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде вариационного ряда.
Равноотстоящиминазывают варианты, которые образуют арифметическую прогрессию с разностью h.
Условныминазывают варианты, определяемые равенством
ui=(xi-C)/h,
где С—ложный нуль (новое начало отсчета); h — шаг, т. е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).
Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.
Покажем, что если вариационный ряд состоит из равноотстоящих вариант с шагом h, то условные варианты есть целые числа. Действительно, выберем в качестве ложного нуля произвольную варианту, например хт, Тогда
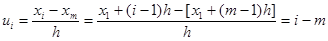 .
.
Так как i и m-целые числа, то их разность i-m = иi-также целое число.
Замечание 1. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
Замечание 2. Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.
Пример.Найти условные варианты статистического распределения:
варианты . . . 23,6 28,6 33,6 38,6 43,6
частоты ... 5 20 50 15 10
Решение. Выберем в качестве ложного нуля варианту 33,6 (этаварианта расположена в середине вариационного ряда). Найдем шаг:
h = 28,6 —23,6 = 5.
Найдем условную варианту:
u1=(xi-C)/h= (23,6 —33,6)/5 = -2.
Аналогично получим: u2= - 1, u3 = 0, u4 =1, u5 = 2. Мы видим, что условные варианты — небольшие целые числа. Разумеется, оперировать с ними проще, чем с первоначальными вариантами.
58. Обычные, начальные и центральные моменты.
Обычным эмпирическим моментом порядка kназывают среднее значение k-x степеней разностей xi - С:

где xi- наблюдаемая варианта, ni- частота варианты,  - объем выборки, С - произвольное постоянное число (ложный нуль).
- объем выборки, С - произвольное постоянное число (ложный нуль).
Начальным эмпирическим моментом порядка kназывают обычный момент порядка k при С = 0
 .
.
В частности,
 ,
,
т, е. начальный эмпирический момент первого порядка равен выборочной средней.
Центральным эмпирическим моментом порядка k называют обычный момент порядка k при С = 
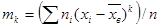 .
.
В частности,
 ,
,
т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.
Легко выразить центральные моменты через обычные:
 ,
,

59. Условные эмпирические моменты.
Условным эмпирическим моментом порядка kназывают начальный момент порядка k,
Дата добавления: 2015-01-19; просмотров: 716; Мы поможем в написании вашей работы!; Нарушение авторских прав |




 называют среднее арифметическое значений признака генеральной совокупности.
называют среднее арифметическое значений признака генеральной совокупности.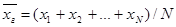 .
. ,
, называют среднее арифметическое значение признака выборочной совокупности.
называют среднее арифметическое значение признака выборочной совокупности.
 ,
, ,
, =(10*1+15*6)/25=4;
=(10*1+15*6)/25=4; = (20*1+30*5)/50 = 3,4.
= (20*1+30*5)/50 = 3,4. .
. ,
,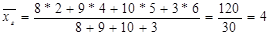 .
. .
.