Две переменные x и y связаны функциональной зависимостью, если для каждого значения одной из них можно получить по определёному правилу одно или несколько значений другой.

Теорема.Линейная средняя квадратическая регрессия Y на X имеет вид

,

где т_х=M(X), т_y=M(Y), , , r = μ_ху /(σ_xσ_y) - коэффициент корреляции величин X и Y.

Доказательство. Введем в рассмотрение функцию двух независимых аргументов и :

.

Учитывая, что М (X—т_х)=М (Y—m_y )= 0, M[(X—m_x)*(Y-m_y)]= μ_ху=r σ_xσ_y,

и выполнив выкладки, получим

.

Исследуем функцию на экстремум, для чего приравняем нулю частные производные:

Отсюда

, .

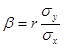Легко убедиться, что при этих значениях и рассматриваемая функция принимает наименьшее значение.

Итак, линейная средняя квадратическая регрессия Y и X имеет вид

,

или

.

Коэффициент называют коэффициентом регрессии Y на X, а прямую

(**)

называют прямой среднеквадратической регрессии Y на X.

62. Статистическая проверка статистических гипотез. Понятие о критериях согласия.

Под статистической гипотезой понимают всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (по результатам наблюдений).

Не располагая сведениями о всей генеральной совокупности, высказанную гипотезу сопоставляют по определенным правилам, с выборочными сведениями и делают вывод о том, можно принять гипотезу или нет.

Процедура сопоставления высказанной гипотезы с выборочными данными называется проверкой гипотезы.

Рассмотрим этапы проверки гипотезы и используемые при этом понятия.

Этап 1. Располагая выборочными данными и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Но, которую называют основной илинулевой, и гипотезу Н₁ конкурирующую с гипотезой Н₀. Термин «конкурирующая» означает, что являются противоположными следующие два события:

по выборке будет принято решение о справедливости для генеральной совокупности гипотезы Н₀;

по выборке будет принято решение о справедливости для генеральной совокупности гипотезы Н₁.

Гипотезу H₁ называют также альтернативной. Например, если нулевая гипотеза такова: математическое ожидание равно 5,- то альтернативная гипотеза может быть следующей: математическое ожидание меньше 5, что записывается следующим образом:

Этап 2. Задаются вероятностью  , которую называют уровнем значимости. Поясним ее смысл.

Решение о том, можно ли считать высказывание Н₀ справедливым для генеральной совокупности, принимается по выборочным данным, т. е. по ограниченному ряду наблюдений, следовательно, это решение может быть ошибочным. При этом может иметь место ошибка двух родов:

отвергают гипотезу Но, или, иначе, принимают альтернативную гипотезу H₁, тогда как на самом деле гипотеза Н₀ верна; это ошибка первого рода;

принимают гипотезу Н₀ , тогда как на самом деле высказывание Но неверно, т. е. верной является гипотеза Н₁ это ошибка второго рода.

Так вот уровень значимости —это вероятность ошибки первого рода, т. е.

вероятность того, что будет принята гипотеза Н₁ , если на самом деле в генеральной совокупности верна гипотеза Но. Вероятность задается заранее малым числом, используют некоторые стандартные значения: 0,05; 0,01; 0,005; 0,001. Например, α=0,05 означает следующее: если гипотезу Но проверять по каждой из 100 выборок одинакового объема, то в среднем в 5 случаях из 100 мы совершим ошибку первого рода.

Вероятность ошибки второго рода обозначают β, т. е.

—вероятность того, что будет принята гипотеза Но, если на самом деле верна гипотеза Н₁.

Этап 3. Находят величину φ такую, что:

ее значения зависят от выборочных данных, т. е. для которой справедливо равенство

ее значения позволяют судить о «расхождении выборки с гипотезой Н₀»; и которая, будучи величиной случайной в силу случайности выборки, подчиняется при выполнении гипотезы Но некоторому известному закону распределения.

Величину φ называют критерием.

Этап 4. Далее рассуждают так. Так как значения критерия позволяют судить о «расхождении выборки с гипотезой Но», то из области допустимых значений критерия следует выделить подобласть  таких значений, которые свидетельствовали бы о существенном расхождении выборки с гипотезой Но и, следовательно, о невозможности принять гипотезу Но.

Подобласть  называют критической областью.

Допустим, что критическая область выделена. Тогда руководствуются следующим правилом: если вычисленное по выборке значение критерия  попадает в критическую область, то гипотеза Но отвергается и принимается гипотеза Н₁. При этом следует понимать, что такое решение может оказаться ошибочным:

на самом деле гипотеза? yо может быть справедливой. Таким образом, ориентируясь на критическую область, можно совершить ошибку первого рода, вероятность которой задана заранее и равна . Отсюда вытекает следующее требование к критической области :

вероятность того, что критерий  примет значениеизкритической области  , должна быть равна заданному числу , т. е.

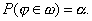
Но критическая область данным равенством определяется неоднозначно. Действительно, представив себе график функции плотности f (х) критерия  , нетрудно понять, что наоси абсцисс существует бесчисленное множество областей-интервалов таких, что площади построенных на них криволинейных трапеций равны . Поэтому кроме требования

выдвигается следующее требование: критическая область  должна быть расположена так, чтобы при заданной вероятности  ошибки первого рода вероятность  ошибки второго рода была минимальной.

2. Критерий согласия Пирсона.

Существуют различные методы проверки гипотез о неизвестных параметрах известных законов распределения. Но чаще на практике закон распределения неизвестен и необходимо выбрать модель закона и проверить возможность принять выдвинутую модель.

Проверка гипотезы о предполагаемом законе осуществляется с помощью специально подобранной СВ, которая называется критерием согласия.

Критерий согласия- это критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Существует несколько критериев. Ограничимся описанием применения критерия Пирсона (²). Этот критерий можно применять для проверки любого закона распределения. В этом состоит его преимущество.

Эмпирические и теоретические частоты обычно различаются. Это различие может быть случайным (незначимым) или неслучайным ( значимым). Если различия неслучайны, то выдвинутая нулевая гипотеза неверна. Критерий Пирсона позволяет ответить на вопрос о значимости или незначимости различий