БИЛЕТ 29. Показатели безотказности восстанавливаемых систем

Восстанавливаемые системы имеют поток отказов и периодически подвергаются воздействию системы технического обслуживания и ремонта. (рис.1.9), где

Процесс эксплуатации

ti — i-ая наработка на отказ.

ti — i-ое время восстановления после i-ого отказа

Случайную величину длительности безотказной работы между соседними периодами восстановления системы можно характеризовать функцией распределения длительности безотказной работы между окончанием восстановления после (i-1)-го отказа и моментом наступления i-го отказа Fi(t). Тогда показатель Qi(t) = Fi(t) будет означать вероятность наступления отказа системы за промежуток времени t после окончания (i-1)-го восстановления. Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t:

.

.

Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа: T_oi

Перечисленные показатели можно назвать локальными. Они характеризуют безотказность в интервалах времени между двумя соседними отказами. Частным случаем локальных показателей безотказности восстанавливаемых систем будут показатели безотказности невосстанавливаемых систем, если рассматривать свойства безотказности до первого отказа

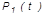
и т.д.

Для общего случая, который учитывает все отказы за интервал времени t, используются общие показатели безотказности, в частности ведущая функция потока отказов

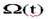
(математическое ожидание случайного числа отказов за время t):

где М – математическое ожидание;

N(t) – случайное число отказов.

Следующий общий показатель безотказности - параметр потока отказов (среднее значение количества отказов в единицу времени за рассматриваемый интервал времени - имеет вид

.

Справедливо обратное соотношение

.

Наглядной характеристикой восстанавливаемых систем является среднее значение параметра потока отказов за рассматриваемую наработку T_P:

Среднюю наработку между отказами восстанавливаемого изделия характеризует показатель Т:

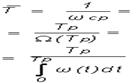
Предел параметра потока отказов

.

Показатель w(t):

.

Если случайные величины наработки между отказами одинаково распределены и независимы (одинаковые законы распределения случайной величины наработки между отказами), т.е. F1(t) = F2(t) = … = Fk(t), то

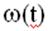
связан с плотностью распределения наработки между отказами f(t) уравнением возобновления

В некоторых случаях удобно искать решение преобразованием Лапласа:

Где

.

Если функция распределения наработки между отказами подчиняется экспоненциальному закону распределения, то расчет значительно упрощается.