Иерархический кластерный анализ. Проблема индексации.

Наряду с обычным, «раздельным», кластерным анализом широко применяется иерархический кластерный анализ, цель которого состоит в получении всей иерархии разбиений, а не отдельного разбиения. Считается, что иерархия точнее характеризует размытую структуру данных, чем отдельное разбиение. Получить конкретное разбиение в случае необходимости сравнительно легко сечением графа иерархий.

Основные определения Пусть О = {O¹, O², …,O^N} – конечное множество объектов. Иерархией h на О называется система подмножеств (классов) {K: K O}такая, что

1) O 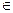h;

2) {Oⁱ} 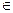h, i=1,2,…,N;

3) для пересекающихся подмножества K и K´, т.е. K K´ ≠ Ø, K K´ либо K´ K.

Пример. Пусть О = {О¹, О²,…, О⁵}. Тогда система подмножеств

h = {{O¹}, {O²}, …,{O⁵}, {O¹,O²}, {O³,O⁴}, {O¹,O²,O⁵}, O}

является иерархией на О.

Иерархия может быть представлена на языке теории графов. Графом иерархии h на О называется ориентированный граф (V,E), вершины v 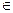V которого соответствуют множествам K 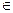h , а ребра e 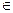E – парам (K´,K), таким что K´ K. Ребро e = (K´,K) изображается стрелкой с началом K´ и концом K.

Иерархической классификацией данного множества объектов

О = {O¹, O², …,O^N} называется построение иерархии h на О, отражающей наличие однородных в определенном смысле классов.

Если использовать неориентированный граф, то его структура становится деревом. Сам процесс классификации есть построение иерархического дерева исследуемой совокупности объектов. Графическое изображение неориентированного графа иерархии на плоскости называют дендрограммой.

В иерархическом кластерном анализе используются два вида алгоритмов: дивизимные и агломеративные. В дивизимных алгоритмах множество О постепенно делится на все более мелкие подмножества, в агломеративных – наоборот: точки множества О постепенно объединяются во все более крупные подмножества. Соответственно графы иерархий, полученные при помощи этих алгоритмов, называют дивизимными и агломеративными. Дивизимные алгоритмы называют также нисходящими (движение против стрелок на графе иерархии), агломеративные – восходящими (движение вдоль стрелок). Если на каждом шаге такого алгоритма объединяются только два кластера, то говорят о бинарном агломеративном алгоритме. Далее рассматриваются лишь такие алгоритмы.

Более подробно схема работы бинарного агломеративного алгоритма выглядит следующим образом. Исходное множество О = ={O¹, O², …,O^N} рассматривается как множество одноэлементных кластеров; выбирают два из них, например K_i и K_j, которые наиболее близки в смысле введенной метрики друг другу и объединяют их в один кластер. Новое множество кластеров будет иметь уже
N-1 элемент K₁,K₂,…,{K_i,K_j},…,K_N..

Рассматривая полученное множество в качестве исходного и повторяя процесс, получают последовательные множества кластеров, состоящие из N-2, N-3 и т.д. кластеров.

К достоинствам иерархических процедур относят полноту анализа структуры исследуемого множества наблюдений, возможность наглядной интерпретации проведенного анализа, возможность остановки процедуры при достижении априори заданного числа кластеров. К cущественным недостаткам иерархических процедур следует отнести финальную неоптимальность. Как правило, даже подчиняя каждый шаг работы процедуры некоторому критерию качества разбиения, получающееся в итоге разбиение для любого наперед заданного числа кластеров оказывается весьма далеким в смысле того же самого критерия качества.