Анализ главных компонент. Геометрическая интерпретация.

Геометрическая интерпретация главных компонент. Для n-мерного вектора 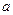с ковариационной матрицей С можно построить так называемый эллипсоид рассеяния: ,

где 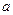– вектор средних значений элементов .

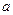Точки, соответствующие наблюдениям вектора а, будут располагаться примерно в очертаниях этого эллипсоида. На рис. 11 приведена двумерная иллюстрация эллипсоида рассеяния.

В методе главных компонент исходные наблюдения предполагаются центрированными. Переход к центрированным наблюдениям означает перенос начала координат в точку 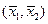. Затем оси координат поворачивают на угол 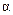так, чтобы ось 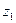шла вдольглавной оси эллипсоида рассеяния. Наблюдения в новых координатах 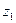и 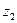станут независимыми.

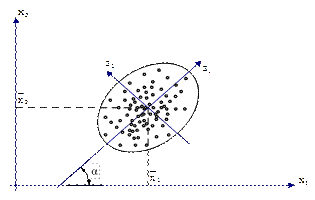
Рис.11. Двумерный эллипсоид рассеяния

Чем теснее наблюдения группируются около главной оси эллипсоида рассеяния, являющейся теперь новой координатой 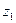, тем менее значащим является для исследователя разброс точек в направлении оси 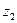, а следовательно, и сама эта координата (рис.12).

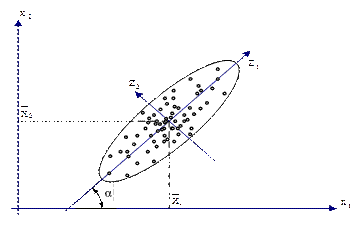
Рис.12. «Вытянутый» эллипсоид рассеяния

Дата добавления: 2015-01-19; просмотров: 47; Нарушение авторских прав