
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многомерные методы экспериментальной оптимизации.
Для поиска экстремума функции многих переменных применяется ряд методов, среди которых отметим:
метод покоординатной оптимизации; метод Бокса − Уилсона; последовательный симплексный метод.
Метод покоординатной оптимизацииМетод покоординатной оптимизации, называемый также методом Гаусса–Зейделя, сводит многомерную оптимизацию к последовательному применению одномерной к сечениям функции. Для этого фиксируют значения всех переменных, кроме одной, к которой применяется один из методов одномерной оптимизации. Затем начинают поиск по второй переменной, фиксируя первую на значении, обеспечившем экстремум, и т. д. После того как список переменных исчерпался, возвращаются к первой переменной, и так до тех пор, пока значение отклика возрастает (убывает). Метод отличается простотой, однако для функций овражистого типа, для которых линии равного уровня сильно вытянуты в направлении, не параллельном осям координат, поиск может продолжаться довольно долго. Метод Бокса−УилсонаНа основе малой серии опытов строится линейное описание поверхности отклика в окрестности начальной точки. В центре этой локальной области определяется значение градиента, после чего начинаются опыты в направлении градиента. Бокс и Уилсон предложили использовать дробные факторные планы для поиска линейной модели. Метод состоит из последовательности циклов, каждый из которых содержит два шага.
1. Построение линейной модели в окрестности некоторой начальной точки  с использованием подходящего факторного плана. Окрестность начальной точки, определяемая интервалами варьирования переменных, должна быть не слишком малой, чтобы можно было выявить линейные эффекты на фоне случайных возмущений, и не настолько большой, чтобы обеспечить адекватность линейного приближения. Соотношение между интервалами варьирования
с использованием подходящего факторного плана. Окрестность начальной точки, определяемая интервалами варьирования переменных, должна быть не слишком малой, чтобы можно было выявить линейные эффекты на фоне случайных возмущений, и не настолько большой, чтобы обеспечить адекватность линейного приближения. Соотношение между интервалами варьирования 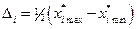 по отдельным переменным должно быть таким, чтобы величины коэффициентов регрессии в случае их значимости имели бы одинаковый порядок. В случае адекватности линейной модели
по отдельным переменным должно быть таким, чтобы величины коэффициентов регрессии в случае их значимости имели бы одинаковый порядок. В случае адекватности линейной модели  коэффициенты регрессии
коэффициенты регрессии 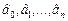 совпадают с компонентами градиента, т.е.
совпадают с компонентами градиента, т.е. 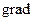
 , где i, j,…,k – направляющие векторы осей координат. Обычно переходят к нормированному градиенту делением его компонент на норму
, где i, j,…,k – направляющие векторы осей координат. Обычно переходят к нормированному градиенту делением его компонент на норму  либо просто на
либо просто на  . Компоненты нормированного градиента обозначим
. Компоненты нормированного градиента обозначим  .
.
2. Пошаговое увеличение величины целевой функции (движение в направлении градиента). Координаты точки наблюдения на  -м шаге при движении в направлении градиента определяются по формуле:
-м шаге при движении в направлении градиента определяются по формуле:  , где
, где  ≥1 – параметр, позволяющий управлять величиной шага, а следовательно, скоростью движения. Чем ближе исследователь подходит к стационарной области, тем меньше
≥1 – параметр, позволяющий управлять величиной шага, а следовательно, скоростью движения. Чем ближе исследователь подходит к стационарной области, тем меньше  . Движение в направлении градиента продолжается до тех пор, пока возрастают значения выходной переменной. В противном случае вновь реализуют факторный план, находят новое линейное приближение и цикл повторяется снова. Если же модель оказывается неадекватной, то это означает, что исследователь либо достиг стационарной области, либо необходимо линейную модель дополнить взаимодействиями. В стационарной области метод Бокса−Уилсона неработоспособен, здесь необходимо переходить к квадратичным моделям.
. Движение в направлении градиента продолжается до тех пор, пока возрастают значения выходной переменной. В противном случае вновь реализуют факторный план, находят новое линейное приближение и цикл повторяется снова. Если же модель оказывается неадекватной, то это означает, что исследователь либо достиг стационарной области, либо необходимо линейную модель дополнить взаимодействиями. В стационарной области метод Бокса−Уилсона неработоспособен, здесь необходимо переходить к квадратичным моделям.
Геометрическая интерпретация метода приведена на рис.4. Здесь поверхность отклика задается линиями уровня.
|
|

| |
| |

Рис. 4. Схема метода Бокса–Уилсона
Рассмотрим в качестве примера использование метода Бокса−Уилсона для поиска максимума функции
 . (6.11)
. (6.11)
Допустимая область изменения переменных: 0£х1£20, 0£х2£10, 1£х3£15. Начальная точка поиска х0=  =(3,2,4). Линейное приближение будем строить в окрестности начальной точки, задаваемой условиями:
=(3,2,4). Линейное приближение будем строить в окрестности начальной точки, задаваемой условиями: 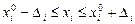 , i=1,2,3. Значения Di желательно подбирать такими, чтобы приращения функции по каждому из аргументов были сопоставимы, то есть
, i=1,2,3. Значения Di желательно подбирать такими, чтобы приращения функции по каждому из аргументов были сопоставимы, то есть

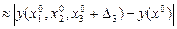 . Примем D1=1, D2=2, D3=3. В соответствии с (6.1) стандартизованная переменная
. Примем D1=1, D2=2, D3=3. В соответствии с (6.1) стандартизованная переменная 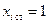 , если
, если  , и
, и  при
при 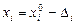 .
.
Линейная модель  требует для своей оценки не менее четырех экспериментов. Воспользуемся ДФЭ 23-1 с ГС:
требует для своей оценки не менее четырех экспериментов. Воспользуемся ДФЭ 23-1 с ГС:  (табл. 16).
(табл. 16).
Таблица 16
| i | х1ст | х1 | х2ст | х2 | х3ст | х3 | y 
|
| 40,8 | |||||||
| -1 | -1 | 26,2 | |||||
| -1 | -1 | 24,4 | |||||
| -1 | -1 | 25,4 |
В последнем столбце табл.16 содержатся значения функции (6.11) для исходных переменных, то есть 40,8=у(4,4,7) и так далее.
МНК-оценки коэффициентов линейной модели составят:
 ;
;  ;
;  .
.
Отнормируем полученные компоненты градиента, поделив их на максимальное значение  :
:  b1=3,4/4,3=0,79, b2=1, b3=0,91. Движение в направлении градиента представлено в табл.17.
b1=3,4/4,3=0,79, b2=1, b3=0,91. Движение в направлении градиента представлено в табл.17.
Таблица 17
| Формулы для вычисления компонент вектора | Номера компонент вектора | у | ||
| 1-я | 2-я | 3-я | ||
| х0 | 31,3 | |||
| Di | ||||
| bi | 0,79 | 0,91 | ||
| bi´Di | 0,79 | 2,73 | ||
| x0+1´bi´Di | 3,79 | 6,73 | 39,9 | |
| x0+2´bi´Di | 4,58 | 9,46 | 46,4 | |
| x0+3´bi´Di | 5,37 | 12,19 | 50,6 | |
| x0+4´bi´Di | 6,16 | 14,91 | 52,6 |
Движение в направлении градиента после четвертого шага невозможно из-за ограничения на х3. Теперь следует определить градиент в точке x0+3´bi´Di. Поскольку темп роста функции замедлился на последних шагах, область линейного описания следует сузить, уменьшив значения Di.
Дата добавления: 2015-01-19; просмотров: 289; Мы поможем в написании вашей работы!; Нарушение авторских прав |