
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель Белла-ЛаПадулы. Основная теорема безопасности Белла-ЛаПадулы.
Данная модель была предложена в 1975 году для формализации механизмов мандатного управления доступом. Мандатный принцип разграничения доступа, в свою очередь, ставил своей целью перенести на автоматизированные системы практику секретного документооборота, принятую в правительственных и военных структурах, когда все документы и допущенные к ним лица ассоциируются с иерархическими
уровнями секретности.
В модели Белла-ЛаПадулы по грифам секретности распределяются субъекты и объекты, действующие в системе, и при этом выполняются следующие правила:
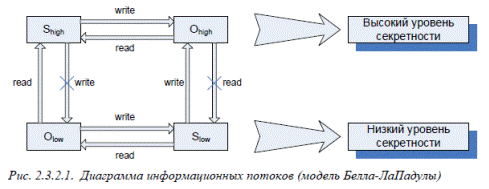
1. Простое правило безопасности (Simple Security, SS). Субъект с уровнем секретности xs может читать информацию из объекта суровнем секретности xo тогда и только тогда, когда xs преобладает над xo.
2. *-свойство (*-property). Субъект с уровнем секретности xs может писать информацию в объект с
уровнем секретности xo в том и только в том случае, когда xo преобладает над xs.
Для первого правила существует мнемоническое обозначение No Read Up, а для второго – No Write Down. Диаграмма информационных потоков, соответствующая реализации модели Белла- ЛаПадулы в системе с двумя уровнями секретности, приведена на рис. 2.3.2.1.
Перейдём к формальному описанию системы. Введём следующие обозначения:
- S – множество субъектов;
- O – множество объектов, S ⊂ O;
- R={r, w} – множество прав доступа, r – доступ на чтение, w – доступ на запись;
- L={U, SU, S, TS} – множество уровней секретности, U- Unclassified, SU – Sensitive but unclassified, S – Secret, TS – Top secret;
- Λ = (L,≤,•,⊗) - решётка уровней секретности;
- V – множество состояний системы, представляемое в виде набора упорядоченных пар (F, M), где:
F : S ∪O → L - функция уровней секретности, ставящая в соответствие каждому объекту и субъекту в системе определённый уровень секретности;
M – матрица текущих прав доступа. Остановимся более подробно на решётке уровней секретности. Напомним, что решёткой Λназывается алгебраическая система вида (L,≤,•,⊗) , где:
- ≤ - оператор, определяющий частичное нестрогое отношение порядка для уровней секретности;
- • - оператор наименьшей верхней границы;
- ⊗ - оператор набольшей нижней границы.
Отношение ≤ обладает следующими свойствами:
1. Рефлексивность: ∀a∈ L : a ≤ a .
С точки зрения уровней безопасности это означает, что разрешена передача информации между субъектами и объектами одного уровня безопасности.
2. Антисимметричность: 1 2 1 2 2 1 2 1 ∀a , a ∈ L : ((a ≤ a )&(a ≤ a ))→ a = a .
Антисимметричность в нашем случае означает, что если информация может передаваться как от субъектов и объектов уровня A к субъектам и объектам уровня B, так и от субъектов и объектов уровня B к субъектам и объектам уровня A, то эти уровни эквивалентны.
3. Транзитивность: 1 2 3 1 2 2 3 1 3 ∀a , a , a ∈ L : ((a ≤ a )&(a ≤ a ))→ a ≤ a .
Транзитивность означает, что если информации может передаваться от субъектов и объектов уровня A к субъектам и объектам уровня B, и от субъектов и объектов уровня B к субъектам и объектам уровня C, то она может передаваться от субъектов и объектов уровня A к субъектам и объектам уровня C. Операторы наименьшей верхней границы • и наибольшей нижней границы ⊗ определяются следующим образом:
- ( , )&( ' : ( ' ) ( ' ' )) 1 2 1 2 1 2 a = a • a ⇔ a a ≤ a ∀a ∈ L a ≤ a → a ≤ a ∨ a ≤ a ;
- ( , )&( ' : ( ' & ' ) ( ' )) 1 2 1 2 1 2 a = a ⊗a ⇔ a ≤ a a ∀a ∈ L a ≤ a a ≤ a → a ≤ a .
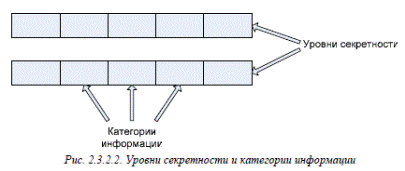
Нетрудно показать, что для каждой пары a a ∈ L 1, 2 существует единственный элемент наименьшей верхней границы и единственный элемент наибольшей нижней границы.Заметим, что в качестве уровней безопасности совершенно не обязательновыбирать целые числа, в ряде случаев удобнее использовать более сложные структуры. Засчёт этого, например, в пределах каждого уровня секретности можно реализоватькатегории секретности (см. рис. 2.3.2.2). В этом случае наличие допуска к той или иной
категории информации может служить дополнительным механизмом безопасности, ограничивающим доступ к защищаемым субъектам или объектам.
Система ( , , ) 0 Σ = v R T в модели Белла-ЛаПадулы состоит из следующих элементов:
- v0 – начальное состояние системы;
- R – множество прав доступа;
- T :V × R →V - функция перехода, которая в ходе выполнения запросов переводит систему из одного состояния в другое.
Изменение состояний системы во времени происходит следующим образом: система, находящаяся в состоянии v∈V , получает запрос на доступ r ∈ R и переходит в состояние v∗ = T(v, r) .
Состояние vn называется достижимым в системе ( , , ) 0 Σ = v R T , если существует последовательность {( , ),..., ( , ),( , )}: ( , ) 0, 1 0 0 1 1 1 = ∀ = − − − + r v r v r v T r v v i n n n n n i i i . Начальное состояние v0 является достижимым по определению. Состояние системы (F, M) называется безопасным по чтению (или simple-безопасным), если для каждого субъекта, осуществляющего в этом состоянии доступ по чтению к объекту, уровень безопасности субъекта доминирует над уровнем безопасности объекта:
∀s∈ S,∀o∈O, r ∈M[s,o]→ F(o) ≤ F(s) .
Состояние (F, M) называется безопасным по записи (или * - безопасным) в случае, если для каждого субъекта, осуществляющего в этом состоянии доступ по записи к объекту, уровень безопасности объекта доминирует над уровнем безопасности субъекта:
∀s∈ S,o∈O : w∈M[s,o]→ F(s) ≤ F(o) .
Состояние (F, M) называется безопасным, если оно безопасно по чтению и по записи. Наконец, система ( , , ) 0 Σ = v R T называется безопасной, если её начальное состояние v0 безопасно, и все состояния, достижимые из v0 путём применения конечной последовательности запросов из R, безопасны.
Теорема(Основная теорема безопасности Белла-ЛаПадулы). Система ( , , ) 0 Σ = v R T безопасна тогда и только тогда, когда выполнены следующие условия:
1. Начальное состояние v0 безопасно.
2. Для любого состояния v, достижимого из v0 путём применения конечной последовательности запросов из R, таких, что T(v, r) = v∗ , v=(F, M) и v∗ = (F ∗ ,M ∗ ) , для ∀s∈ S,∀o∈O выполнены условия:
1. Если r ∈M ∗[s,o] и r ∉M[s,o], то F∗ (o) ≤ F∗ (s) .
2. Если r ∈M[s,o]и F∗ (s) < F ∗ (o) , то r ∉M ∗[s,o] .
3. Если w∈M ∗[s,o] и w∉M[s,o] , то F∗ (s) ≤ F∗ (o) .
4. Если w∈M[s,o] и F∗ (o) < F ∗ (s) , то w∉M ∗[s,o].
Пусть система ( , , ) 0 Σ = v R T безопасна. В этом случае начальное состояние v0 безопасно по определению. Предположим, что существует безопасное состояние v∗,достижимое из состояния v: T(v, r) = v∗ , и для данного перехода нарушено одно изусловий 1-4. Легко заметить, что в случае, если нарушены условия 1 или 2, то состояние v∗ будет небезопасным по чтению, а если нарушены условия 3 или 4 – небезопасным позаписи. В обоих случаях мы получаем противоречие с тем, что состояние v∗ являетсябезопасным.
Докажем достаточность утверждения. Система ( , , ) 0 Σ = v R T может бытьнебезопасной в двух случаях:
1. В случае если начальное состояние v0 небезопасно. Однако данное утверждение противоречит условию теоремы.
2. Если существует небезопасное состояние v∗ , достижимое из безопасного состояния v0 путём применения конечного числа запросов из R. Это означает, что на каком-то промежуточном этапе произошёл переход T(v, r) = v∗ , где v – безопасное состояние, а v∗ - небезопасное. Однако условия 1-4 делают данный переход невозможным.
Отметим, что изложенная модель в силу своей простоты имеет целый ряд серьёзных недостатков. Например, никак не ограничивается вид функции перехода T – а это означает, что можно построить функцию, которая при попытке запроса на чтения к объекту более высокого уровня секретности до проверки всех правил будет понижать уровень секретности объекта. Другим принципиальным недостатком модели Белла-ЛаПадулы является потенциальная возможность организации скрытых каналов передачи информации. Тем самым, дальнейшее развитие моделей мандатного управления доступом было связано с поиском условий и ограничений, повышающих её безопасность.
В настоящее время модель Белла-ЛаПадулы и другие модели мандатного управления доступом, широко используются при построении и верификации автоматизированных систем, преимущественно предназначенных для работы с информацией, составляющей государственную тайну.
Дата добавления: 2015-01-19; просмотров: 695; Мы поможем в написании вашей работы!; Нарушение авторских прав |