
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сформулируйте и докажите теорему Эйлера.
Теорема 4 (теорема Эйлера). Пусть В, Р, Г – число вершин, рёбер и граней соответственно. Тогда для любого плоского связного графа В – Р + Г = 2.
Доказательство. Проведём индукцию по числу рёбер Р. Если Р = 1, то либо это петля, и тогда В = 1, Г = 2, В – Р + Г = 2; либо это ребро, соединяющее 2 разные вершины, и тогда В = 2, Г = 1, В – Р + Г = 2. База индукции имеется. Предполагаем, что для графов с числом рёбер Р – 1 теорема верна. Добавим к такому графу одно ребро так, чтобы граф остался связным. Это можно сделать тремя способами.
1) Новое ребро – петля у одной из вершин. Добавляется 1 ребро и 1 грань, величина В – Р + Г не изменяется.
2) Новое ребро соединяет 2 разные вершины графа. Но граф плоский, и это ребро можно провести так, что оно не пересекает других рёбер, лежит в одной грани и делит её на две. Снова добавляется 1 ребро и 1 грань, величина В – Р + Г не изменяется.
3) Новое ребро инцидентно только одной из вершин графа. Тогда приходится добавлять новую вершину. Если она не лежит на ребре графа, то добавляется 1 ребро и 1 вершина, число граней не изменяется, величина В – Р + Г не изменяется. Если же новая вершина лежит на ребре, то это ребро делится на 2, грань делится на 2 грани. В этом случае добавляется 2 ребра, 1 грань и 1 вершина, величина В – Р + Г опять не изменяется.
27. Что такое правильная раскраска и хроматическое число графа?
Пусть G=( A,V) – неориентированный граф без петель, C c1 ,c2 , ,ck
– некоторое конечное множество – множество «цветов». Правильной раскраской графа называется такое отображение A-> C , что смежные вершины получают разные цвета. Наименьшее число k , при котором существует правильная раскраска, называется хроматическим числом графа: гамма(G)= k (стр.39)
28. Опишите алгоритм обхода графа «в глубину».
Поиск «в глубину» Начинаем обход графа с произвольной вершины. На каждом шаге алгоритма осуществляется переход от текущей вершины к смежной с ней. Если все смежные уже просмотрены, то происходит возврат к предыдущей вершине и поиск смежных с ней. Удобно организовать это с помощью стека, помещая в него «проверенную» вершину и удаляя «использованную» – вершину, для которой все смежные уже проверены.
Пример
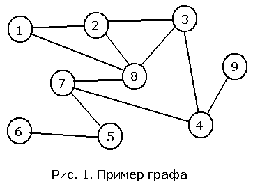
Рассмотрим граф с рис. 1. Начав обход в глубину в вершине 1, мы затем посетим последовательно вершины 2, 3, 4, 7, 5 и 6 и упремся в тупик. Затем нам придется вернуться в вершину 7 и обнаружить, что вершина 8 осталась непосещенной. Однако, перейдя в эту вершину, мы немедленно вновь оказываемся в тупике. Вернувшись в вершину 4, мы обнаруживаем, что непосещенной осталась вершина 9; ее посещение вновь заводит нас в тупик. Мы снова возвращаемся назад в исходную вершину, и поскольку все соседние с ней вершины оказались посещенными, обход закончен.
29. Опишите алгоритм обхода графа «в ширину».
Поиск «в ширину» Основная идея поиска «в ширину»: для данной вершины рассматриваются все смежные с ней, а затем происходит переход к другой вершине. Чтобы организовать такой процесс, нужен не стек, а очередь. Сначала заносится в очередь («проверяется») начальная вершина. Затем проверяются, заносятся в очередь смежные с ней. Когда все смежные проверены, вершина удаляется из очереди. Начинается проверка вершин, смежных с первой в очереди вершиной. Алгоритм заканчивает работу, когда все вершины проверены. Можно использовать алгоритм поиска «в ширину» для построения кратчайших маршрутов от начальной вершины до всех остальных. Такой маршрут можно зафиксировать сразу, как только вершина попадает в очередь, так как известна «предыдущая» (она первая в очереди), и кратчайший маршрут до неё уже построен.
Пример
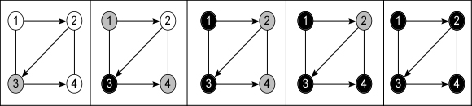
Имеем смешанный граф (см. рис.) с |V| = 4 и |E| = 5. Выполним обход его вершин, используя алгоритм поиска в ширину. В качестве стартовой вершины возьмем узел 3. Сначала он помечается серым как обнаруженный, а затем черным, поскольку обнаружены смежные с ним узлы (1 и 4), которые, в свою очередь, в указанном порядке помечаются серым. Следующим в черный окрашивается узел 1, и находятся его соседи – узел 2, который становится серым. И, наконец, узлы 4 и 2, в данном порядке, просматриваются, обход в ширину завершается.
30. Какие алгоритмы для поиска кратчайших путей в графе вы знаете?
Алгоритм Дейкстры
Алгоритм Форда-Беллмана
Алгоритм Флоида
31. В каких случаях применяется алгоритм Форда?
Если рассматривать графы, у которых, возможно, есть рёбра с отрицательными ве-
сами, то для решения той же задачи приходится применять другие алгоритмы. Мы по-
знакомимся с алгоритмом Форда-Беллмана, позволяющим находить кратчайшие пути
от одной из вершин (источника) до всех остальных вершин в ориентированном взве-
шенном графе без циклов отрицательной длины.
32. В каких случаях применяется алгоритм Дейкстры?
Ставится задача: найти кратчайшие маршруты от одной из вершин (она на-
зывается источником) до всех остальных вершин графа. Для решения этой задачи мы
рассмотрим алгоритм Дейкстры, который можно применять, если нет рёбер с отрица-
тельными весами. При этом граф может быть как ориентированным, так и неориенти-
рованным.
33. В каких случаях применяется алгоритм Флойда?
Рассмотрим теперь задачу определения кратчайших маршрутов для всех пар вер-
шин графа. Задача решается для ориентированных взвешенных графов без циклов от-
рицательной длины.
34. Как решается задача о числе способов разместить n различных элементов в k различных ячеек?
Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить n–1 способами. Таким образом, существует п(п – 1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней k–й ячейки. Эту ячейку при заполненных первых k – 1 ячейках можно заполнить
n–(k–1) (или n–k+1) способами. Таким образом, все k ячеек заполняются числом способов, равным: n(n-1)(n-2)...(n-k+2)(n-k+1)=n!/(n-k)!
Akn=n!/(n-k)!
35. Как решается задача о числе способов разместить k одинаковых элементов в n различных ячеек?
Выведем формулу для подсчета числа сочетаний. Пусть имеется множество Un и нужно образовать упорядоченное подмножество множества Un, содержащее k элементов (то есть образовать размещение). Делаем это так:
1) выделим какие-либо k элементов из n элементов множества Un Это, согласно сказанному выше, можно сделать Ckn способами;
2) упорядочим выделенные k элементов, что можно сделать Pk=k! способами. Всего можно получить Ckn*Pk вариантов (упорядоченных подмножеств), откуда следует: Akn =Ckn*Pk , то есть Ckn =Akn/Pk = n!/(k!(n-k)!)
36. Как определяются обычная и экспоненциальная производящие функции для числовой последовательности {an} ?
Последовательности {an} - это формальный степенной ряд.
Производящая функция последовательности {an} - это формальный степенной ряд
Беск∑0 беск(an*xn).
Зачастую производящая функция последовательности является рядом Тейлора некоторой аналитической функции.
Производящая функция суммы (или разности) двух последовательностей равна сумме (или разности) соответствующих производящих функций.
Экспоненциальная производящая функция последовательности {an} - это формальный степенной ряд
Беск∑0(an*xn)/n!
37. Как строится производящая функция для последовательности k-сочетаний с повторениями элементов n-множества при различных ограничениях на число повторений?

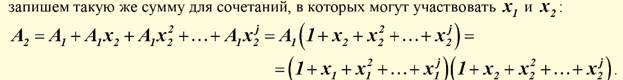

38. Как строится производящая функция для последовательности k-размещений с повторениями элементов n-множества при различных ограничениях на число повторений?

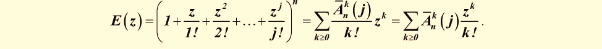

39. Как строятся производящие функции для решения задачи о числе способов размещения элементов по ячейкам?

40. Что такое рекуррентная последовательность?
линейные однородные рекуррентные уравнения (ЛОРУ) с постоянными действительными коэффициентами:
стр 14 . (*)
Здесь p1,p2…….pk – действительные числа, ai – i -й член некоторой последовательности
Число k называется порядком уравнения.
Если a0,a1,.....ak-1 заданы, то из соотношения (*) можно найти сначала k
a , затем a k+1 и так далее, можно определить любой член искомой последовательности. Итак,
уравнение (*) и значения a0,a1,.....ak-1 полностью определяют последовательность.
Дата добавления: 2015-01-19; просмотров: 318; Мы поможем в написании вашей работы!; Нарушение авторских прав |